Кафедра вычислительных методов механики деформируемого тела

Кафедра вычислительных методов механики деформируемого тела

Горх Эдуард Владимирович

Выпускная квалификационная работа бакалавра

Потеря устойчивости мостичного амортизатора из эластомера

Направление 010400

Прикладная математика и информатика

Научный руководитель,
кандидат физ.-мат. наук,
доцент
Кабриц С.А.

Санкт-Петербург

Содержание

Введение................................................................................................. 3

Постановка задачи................................................................................. 4

Обзор литературы................................................................................. 6

Глава 1. Математическая формулировка задачи................................. 7

1.1. Основные зависимости для арки-полоски.................................. 8

1.2. Решение поставленной задачи................................................... 12

Глава 2. Методы численного решения............................................... 15

2.1 Метод стрельбы.......................................................................... 16

2.2 Метод продолжения по параметру............................................ 17

Глава 3. Анализ результатов.............................................................. 18

3.1 Алгоритм нахождения точки бифуркации................................ 18

3.2. Бифуркация................................................................................ 20

3.3. Изолированное решение........................................................... 27

Выводы................................................................................................. 31

Заключение........................................................................................... 32

Список литературы.............................................................................. 33

Введение

Во многих областях современной техники для снижения перегрузок при ударе и изоляции вибраций широко используются различные типы амортизаторов. В одних случаях они защищают основание от действия динамических сил, в других позволяют уменьшить динамические воздействия, передаваемых на амортизируемый объект от движущегося с переменным ускорением основания.

Для поглощения перегрузок, испытываемых конструкцией при ударных воздействиях, необходимо применение амортизаторов, имеющих мягкую характеристику. Такими амортизаторами являются, в частности, амортизаторы мостичного типа. Изменяя геометрические и физические параметры эластомеров, можно изменять вид их упругой характеристики, что особенно важно для противоударных амортизаторов. Наличие значительного внутреннего трения в материале позволяет достичь хорошей виброизоляции в области высоких частот и уменьшить возможность возникновения резонансных колебаний с большими амплитудами.

Основная сложность при расчетах деформаций различных изделий из эластомера возникает из-за нелинейности задачи.

Постановка задачи

В рамках нелинейной теории тонких оболочек из эластомера [4] рассматривается задача о бифуркации мостичного амортизатора при сжатии. Под бифуркацией понимается ответвление от симметричного решения в несимметричное.

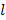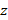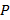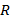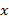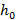Рис. 1. Рассматриваемый мостичный амортизатор

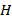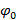Амортизатор представляет собой две симметричные резиновые пластины по бокам, наклоненные под некоторым углом к плоскости симметрии амортизатора. Они привулканизированы к металлическим пластинам снизу (нижнее основание) и сверху (верхнее основание) (рис. 1).

Целью работы является исследовать бифуркации от симметричного состояния при различных конфигурациях системы (рис. 2) и выяснить, при каких начальных углах они возможн­­­ы.

Несимметричная конфигурация

Симметричная конфигурация

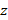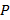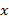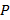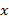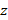Рис. 2. Конфигурации амортизатора при сжатии

В отличии от [1], в качестве краевых условий у верхнего основания рассматривается шарниное опирание. Как показали эксперименты, при вулканизации у верхнего основания реализуется именно шарнирное опирание, а у нижнего – жесткая заделка, на что обратил внимание академик Новожилов В.В. В настоящей работе предполагается, что верхнее основание амортизатора может сдвигаться вбок, оставаясь параллельным нижнему основанию.

Программная реализация решения поставленной задачи написана в среде MATLAB.

Обзор литературы

В 1981 вышла статья [2], в которой исследуется симметричное сжатие мостичного амортизатора. Построены жесткостные характеристики для разных начальных углов и толщин, приведена граница раздела областей мягкой и жесткой характеристик амортизатора. Основы нелинейной теории упругости для эластомеров были заложены Черныхом К.Ф. [3]. В [1] рассмотрена бифуркация подобной модели при условии заделки у верхнего основания. Также, там предполагается, что металлическая пластина имеет возможность поворачиваться.

В [4] группой авторов были изложены основные разделы нелинейной теории упругих оболочек из эластомеров. В работах [5–6] Кабриц С.А. и Колпак Е.П. описывают способы численного поиска точек ветвления и связанные с этим проблемы.

В учебнике [7], Бахвалов Н.С. описал метод стрельбы применительно к решению нелинейных краевых задач для систем дифференциальных уравнений.

В работе [8] подробно излагается приложение метода продолжения по параметру к проблеме неединственности решения нелинейных задач теории упругих оболочек.

В учебнике [9] подробно освещаются вопросы устойчивости механических систем, определяются критические нагрузки, предельные точки и точки бифуркации. Пановко Я.Г. и Губанова И.И. в работе [10] объяснили использование метода деидеализации для нахождения бифуркационных ветвей на примере задачи о внецентренном сжатии стержня.

Различные вопросы о подобных амортизаторах рассматриваются уже в течение многих лет. Например, в вестнике МГТУ им. Баумана в статьях [11–12] рассматривается модель нелинейного плоского напряженного состояния теории упругости при допущении сжимаемости материала. Были проведены расчеты деформаций мостичных амортизаторов с помощью МКЭ.

Решение поставленной задачи

Введем обозначение 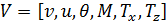для (1.1) и 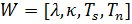для (1.2). Систему дифференциальных уравнений (1.1) можно представить в виде:

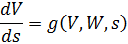(1.4)

а систему (1.2) в виде:

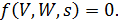(1.5)

Граничные условия (1.3) можно записать в виде:

(1.6)

Задача сводится к решению систем (1.4), (1.5) с граничными условиями (1.6).

Для нахождения точек разветвления решений используется идея метода деидеализации [9]. В данной работе рассматривается два варианта введения неидеальностей:

а) приложение усилия ;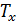

б) фиксированное смещение верхней пластины по оси ,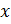

которые ниже будут изложены подробнее.

Алгоритм решения

Задача решается методом стрельбы. Он сводит краевую задачу к задаче Коши. Задача Коши для системы дифференциальных уравнений решается численно методом Рунге – Кутты – Мерсона. Далее методом Ньютона решается система нелинейных уравнений. В качестве начального приближения задается нулевой вектор, так как он является решением для ненагруженного состояния амортизатора. При дальнейшем выборе начальных приближений используетя метод продолжения по параметру. Матрица производных в методе Ньютона считается численно.

Стоит отметить, что, в случае приближения к точке бифуркации, матрицы Якоби становятся плохо обусловленными. В самой точке бифуркации Якобиан принимает нулевое значение, поэтому прохождение по любому из параметров через точку бифуркации становится невозможным.

Метод стрельбы

Суть метода заключается в сведении нелинейной краевой задачи к задаче Коши.

Рассмотрим нелинейную краевую задачу:

	2.1

Пусть функции таковы, что система уравнений:

	2.2

однозначно определяет вектор Тогда задача (2.1) может быть сведена к системе нелинейных уравнений относительно параметров .

Довольно часто грачниное условие в точке 0 имеет вид:

Тогда в качестве целесообразно взять Таким образом, здесь в качестве искомых параметров выступают неизвестные компоненты решения в точке Как правило, тербуемая система нелинейных уравнений не выписывается явно, но можно указать алгоритм вычисления ее правой части.

При каждых , решая систему (2.2) можно определить вектор решая задачу Коши при начальном условии , определяем и затем находим . Таким образом, решение задачи (2.1) сводится к решению нелинейной системы

В этой работе в качестве метода решения нелинейной системы выбран метод Ньютона. При использовании метода Ньютона на каждой итерации численно вычисляется матрица производных.

Глава 3. Анализ результатов

Бифуркация

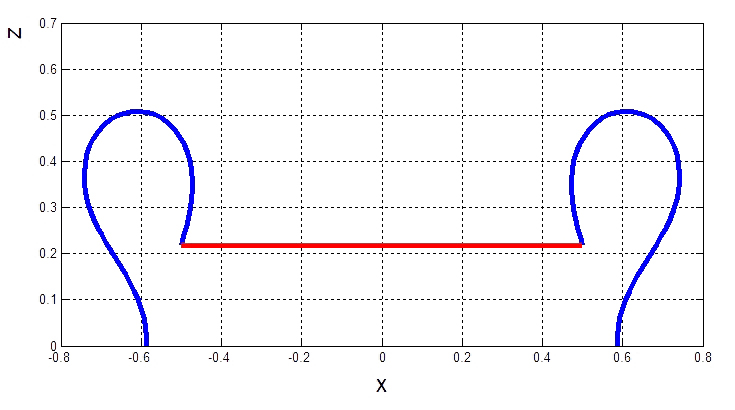
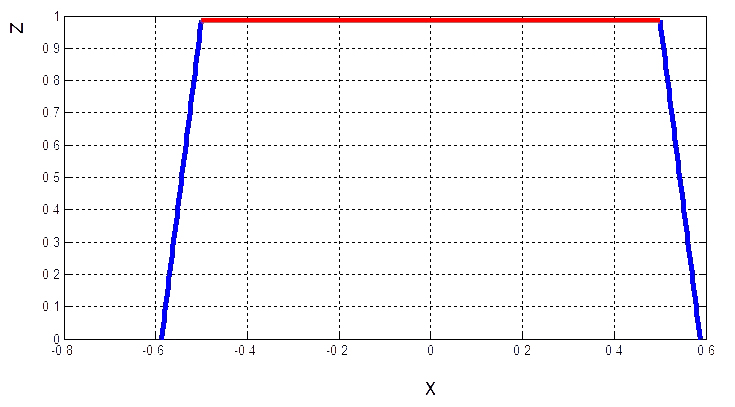
Рис. 8. Амортизатор в плоскости 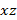, несимметричное сжатие

Рис. 7. Амортизатор в плоскости 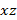, симметричное сжатие

Рассмотрим сжатие амортизатора с начальным углом наклона боковых пластин к оси 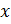равному 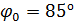(рис. 7–8). На всех приведенных ниже рисунках в качестве боковых пластин проиллюстрированы их срединные линии.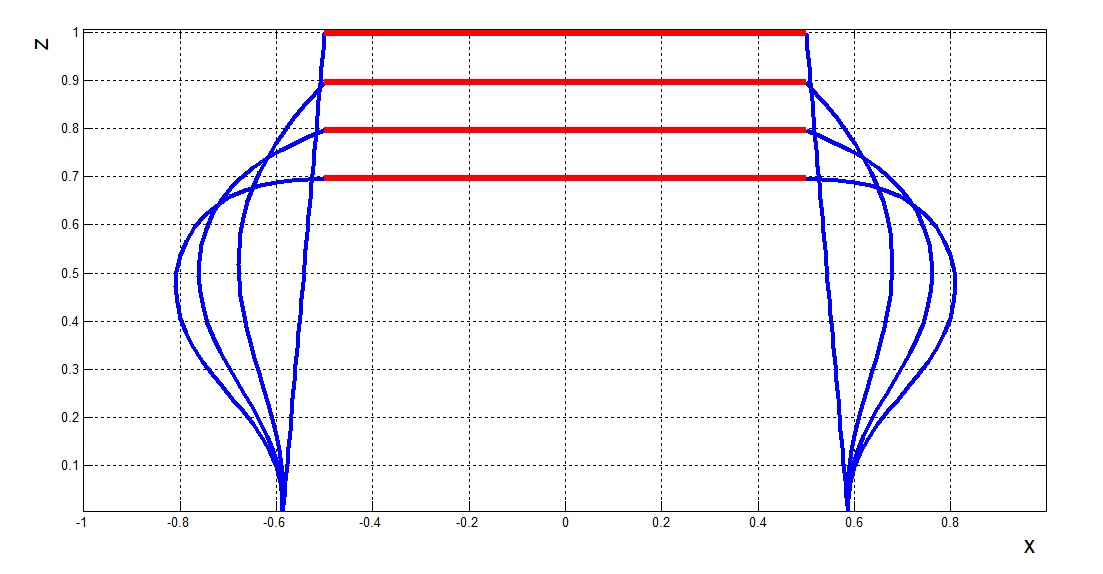

На рисунке 8 несимметричная деформация реализована следующим путем: по оси 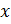к амортизатору приложено усилие .

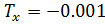P

Далее, амортизатор сжимается дискретно по параметру 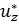до момента, когда угол между касательной в точке скрепления пластин и верхней пластиной не становится равным нулю. Потом, используя метод деидеализации, изложенный выше, 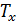приравнивается к нулю и сжимающая нагрузка убирается до момента, пока амортизатор не вернется в состояние покоя. На всех диаграммах, приведенных ниже, проиллюстрирован процесс возврата амортизатора в исходное положение, то есть, движение по параметру 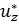осуществляется справа налево.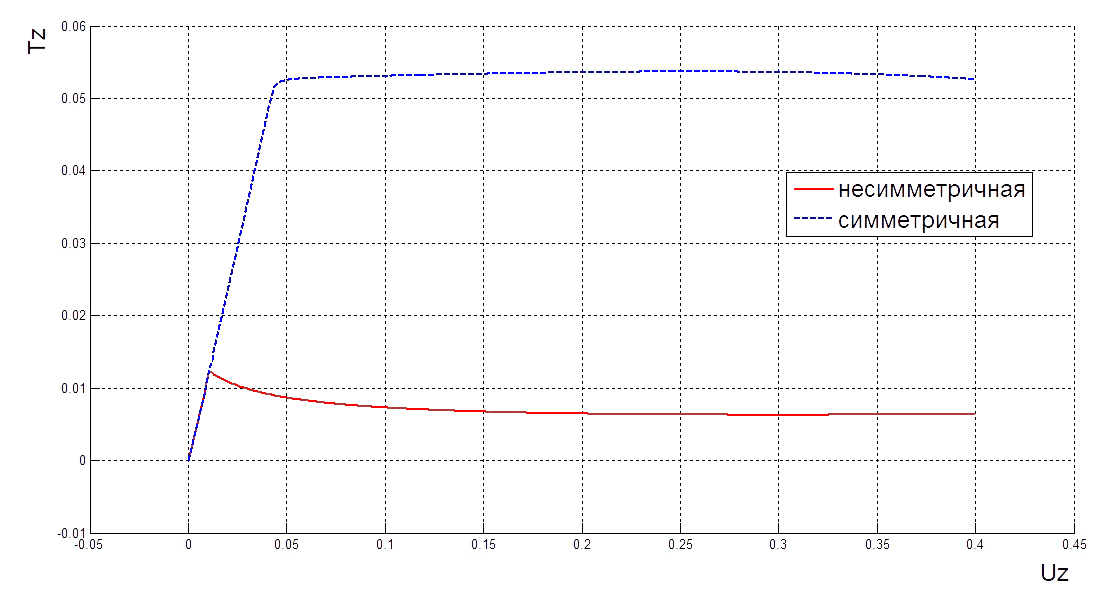

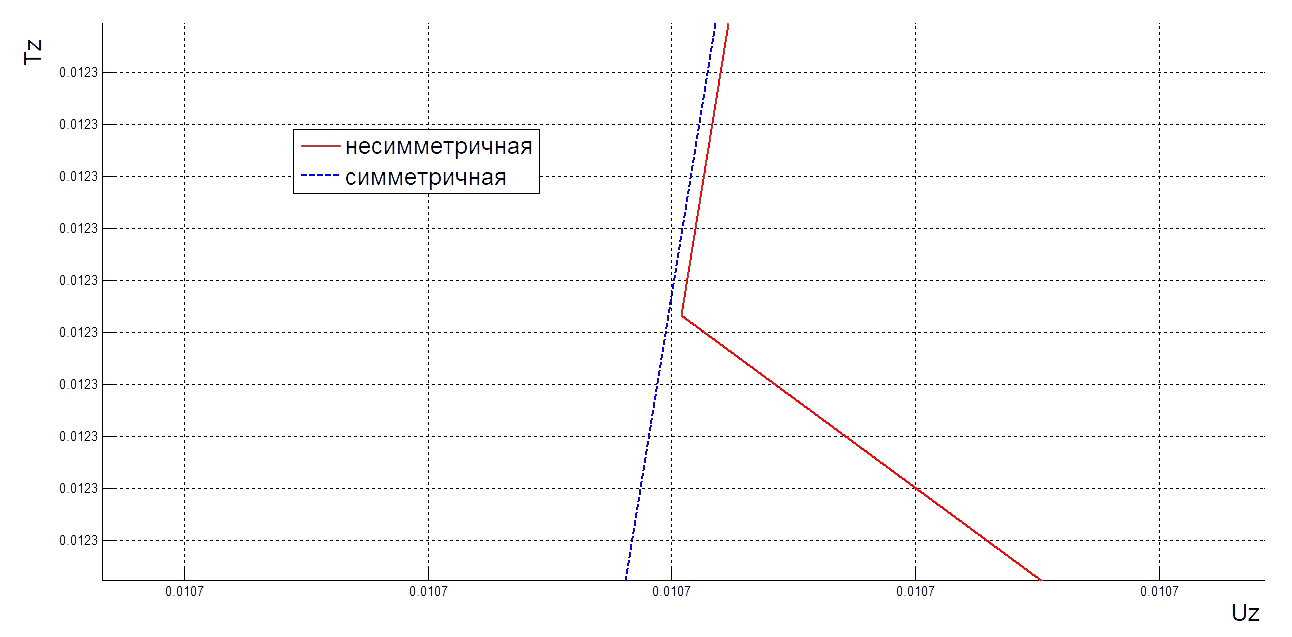
Рис. 9. Диаграмма нагрузка-перемещение

Из рисука 9 видно, что в точке 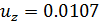графики несимметричной и симметричной форм сливаются в один. Стоит подметить, что несимметричный вариант является выгоднее симметричного, потому что для его реализации нужна меньшая вертикальная нагрузка. Рассмотрим окрестность точки ветвления ближе (рис. 10):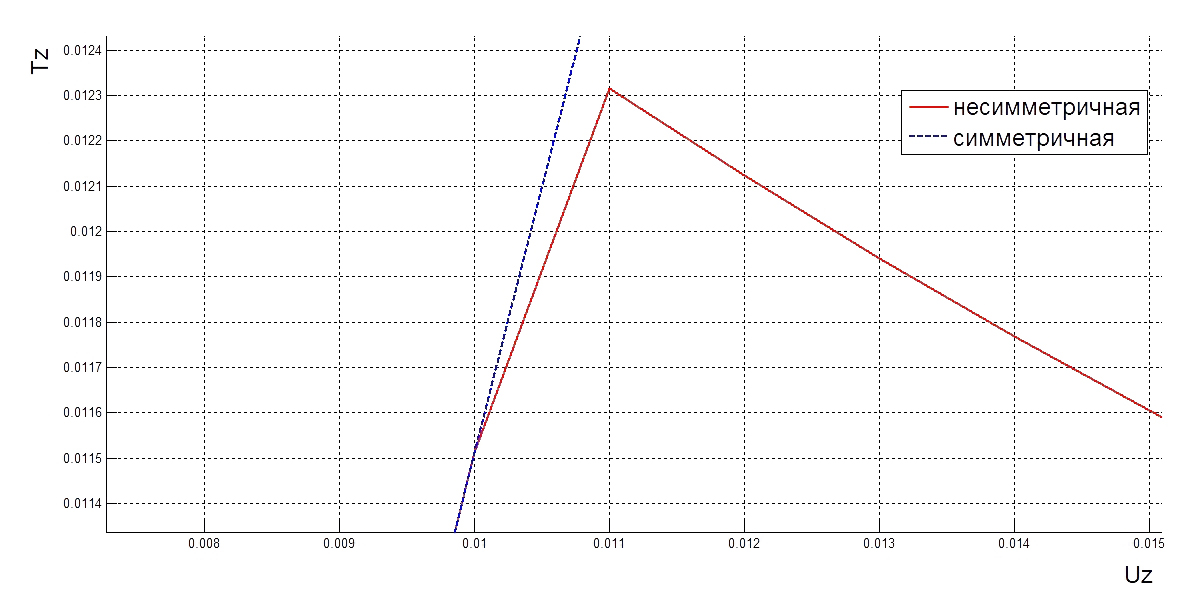

Рис. 10. Диаграмма нагрузка-перемещение

P

На промежутке 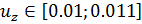(рис. 10) наблюдается численный переско

Рис. 10. Диаграмма нагрузка-перемещение

к. Если в окрестности этой точки шаг параметра уменьшить в 100 раз, то наблюдается то же самое, что и на рисунке 10. При дальнейшем уменьшении шага наблюдается ухудшение сходимости. Следовательно, требуется пройти по другому параметру.

Рис. 17. Диаграмма нагрузка-перемещение

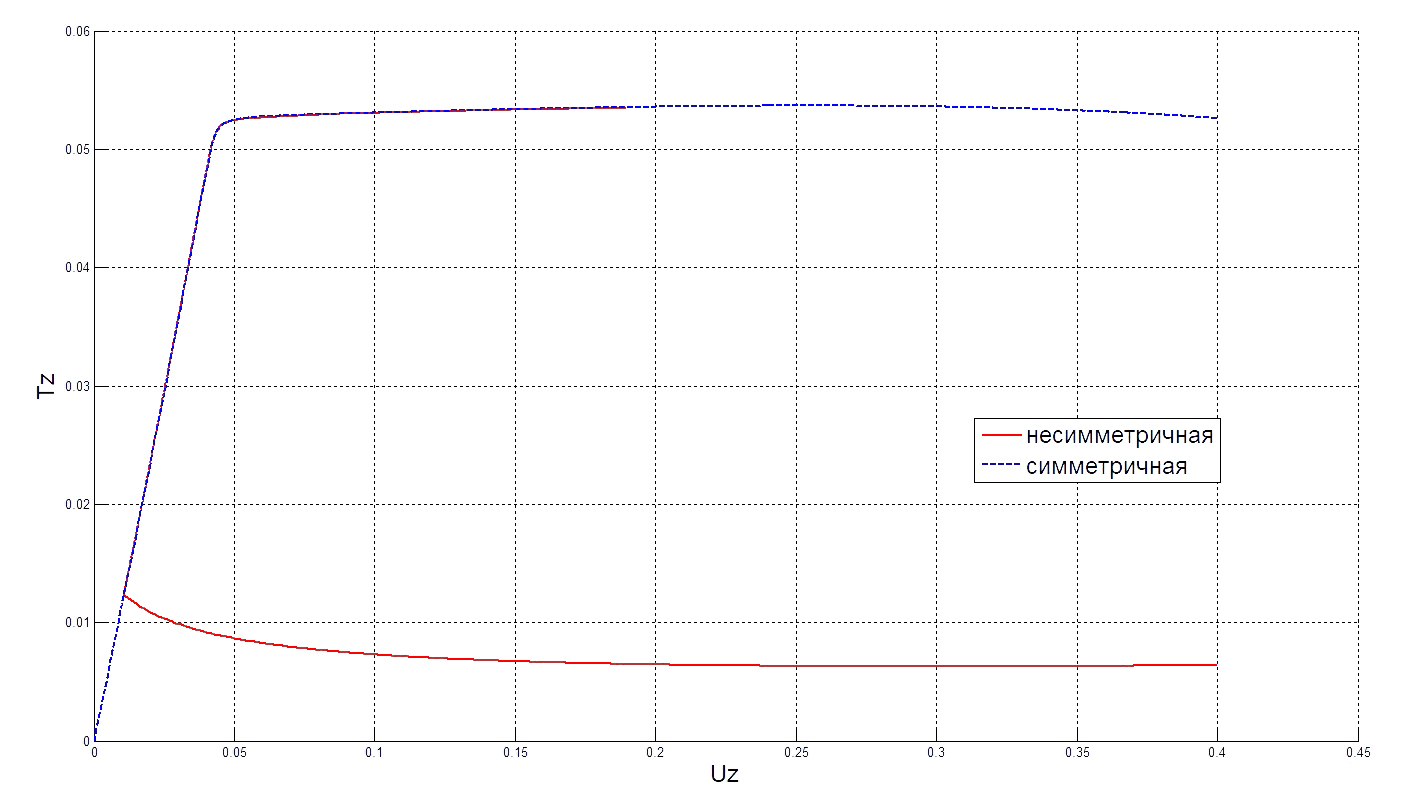
При движении по параметру 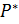– параметру вертикального нагружения (рис. 11) несимметричная ветвь снова перескакивает на симметричную.

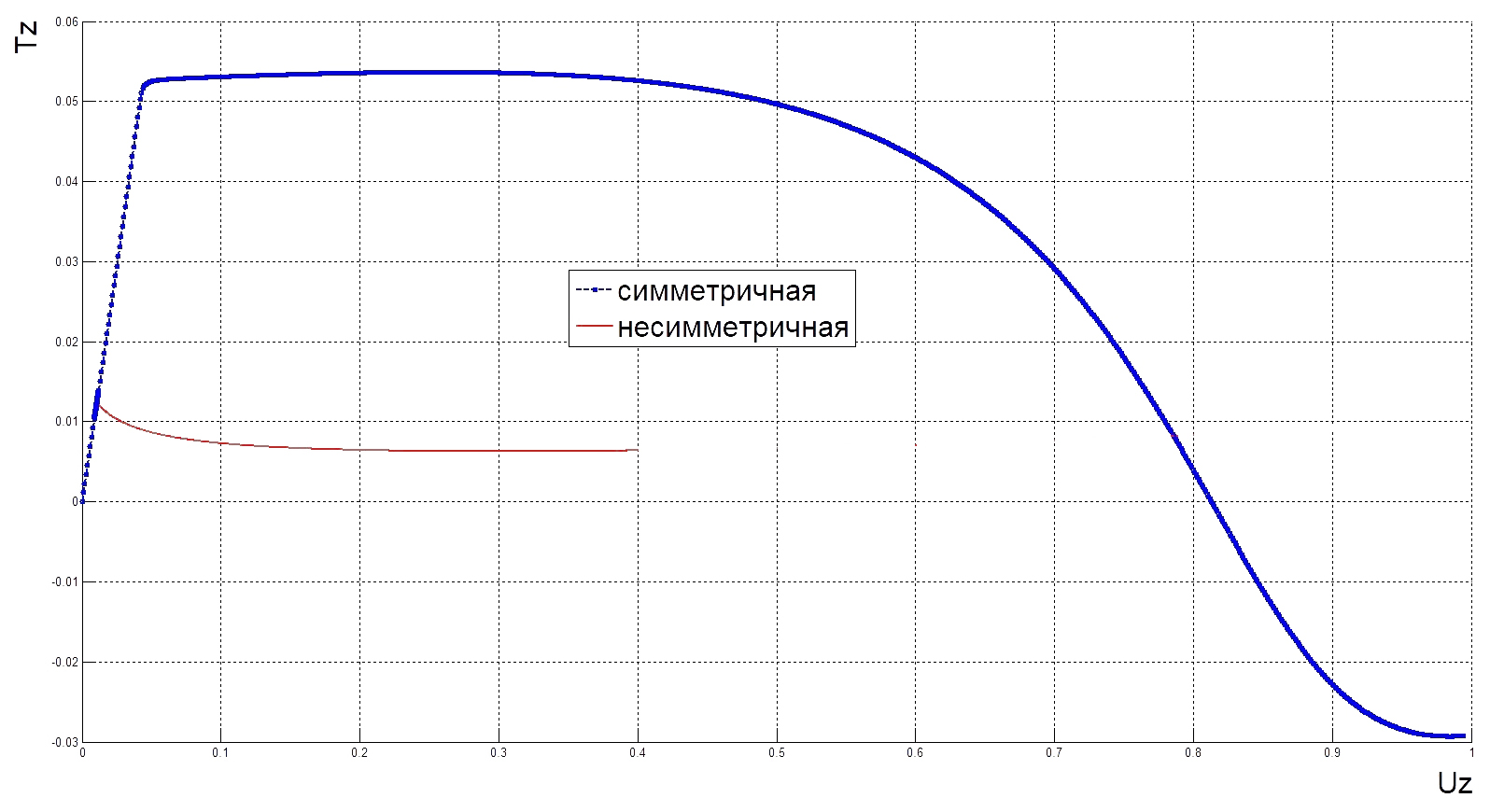
Рис. 11. Диаграмма нагрузка-перемещение

P

P

Рассмотрим точку ветвления ближе (рис. 12):

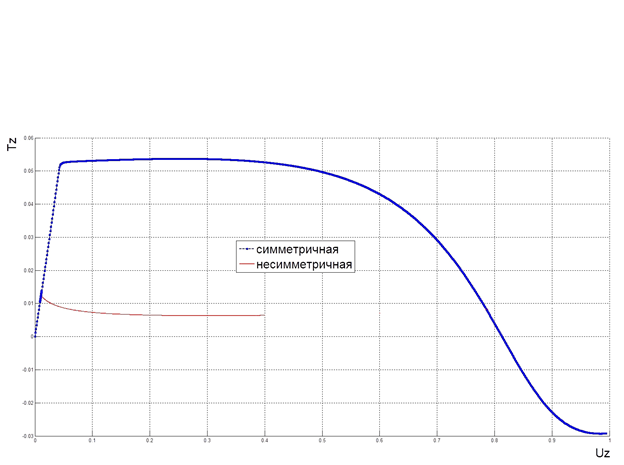
Рис. 12. Диаграмма нагрузка-перемещение

Рис. 13. Диаграмма нагрузка-перемещение

Из рисунков 11–12 видно, что графики совпадают, учитывая погрешность вычисления. Чтобы получить больше данных для полноценного анализа, требуется пройти по еще одному параметру.

Рассмотрим движение по параметру 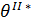– параметру угла поворота (рис. 13). Также, на рисунке 13 симметричное решение продолжено по 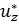до конца высоты амортизатора для дальнейших исследований.

Рассмотрим окрестность точки соединения графиков ближе (рис. 14):

Рис. 14. Диаграмма нагрузка-перемещение

Рис. 15. Диаграмма зависимости от трех параметров продолжения решения

P

P

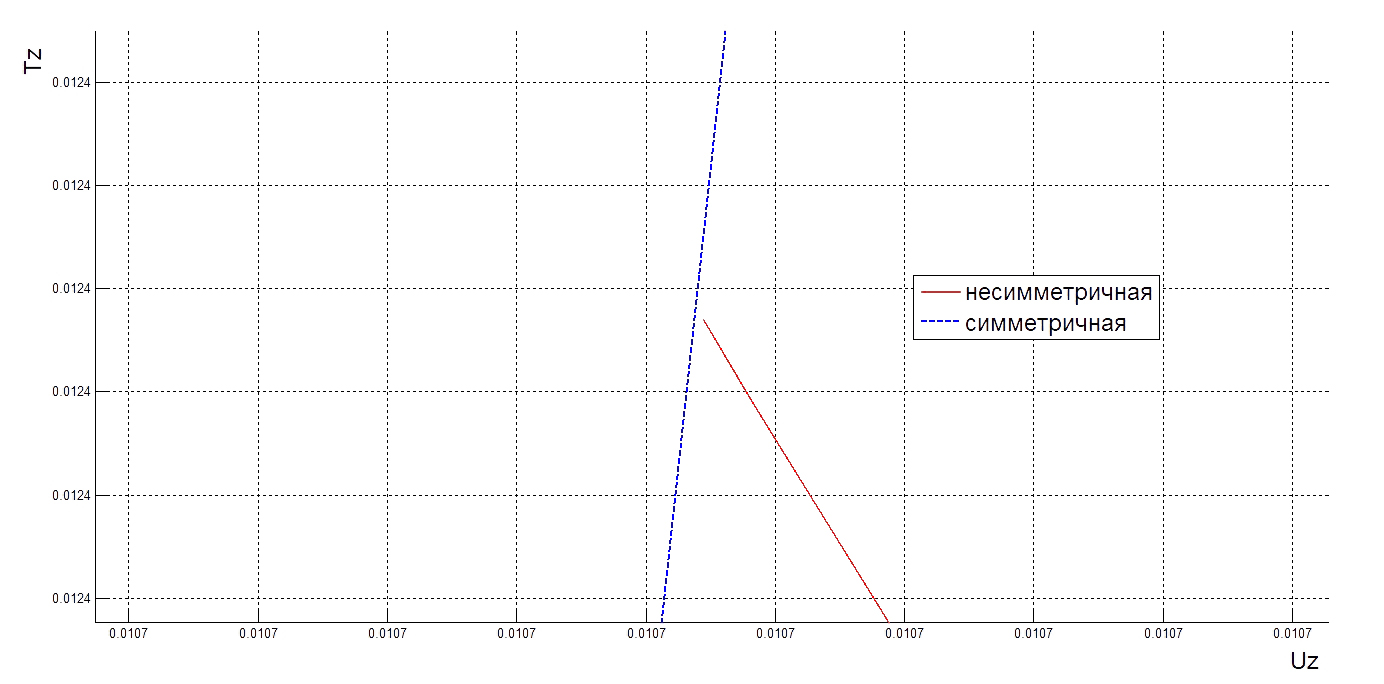
Каким бы мелким ни был шаг, при движении по 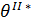наблюдается остановка в окрестности этой точки и «разворот» назад по той же кривой в этой плоскости (рис. 14). То есть, следует рассмотреть трехмерный график зависимости всех от трех параметров (рис. 15).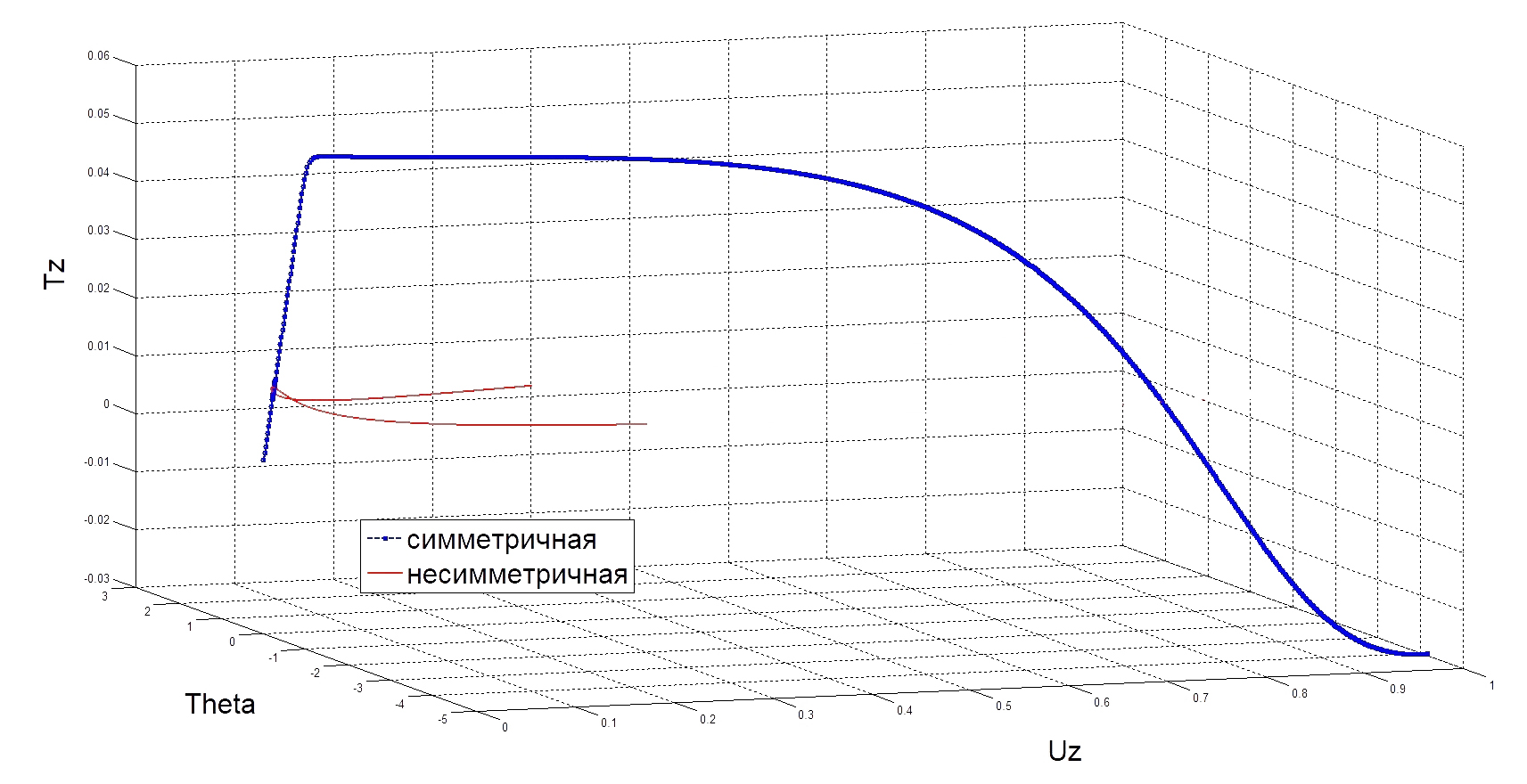

Из рисунков 9, 11 и 13 видно, что при движении по любому параметру не осуществляется плавного перехода на симметричное решение, точка является предельной для всех параметров. Также, если в окрестности этой точки пройти по симметричному варианту с мелким шагом, то наблюдается сильно ухудшение сходимости вплоть до остановки алгоритма. Следовательно, эта точка – точка бифуркации, то есть точка разветвления решения. В ней при нагружении будет происходить переход симметричного варианта на несимметричный.

Рис. 16. Бифуркационная диаграмма нагрузка-поворот

P

Рассмотрим диаграмму (рис. 15) в плоскости (рис. 16).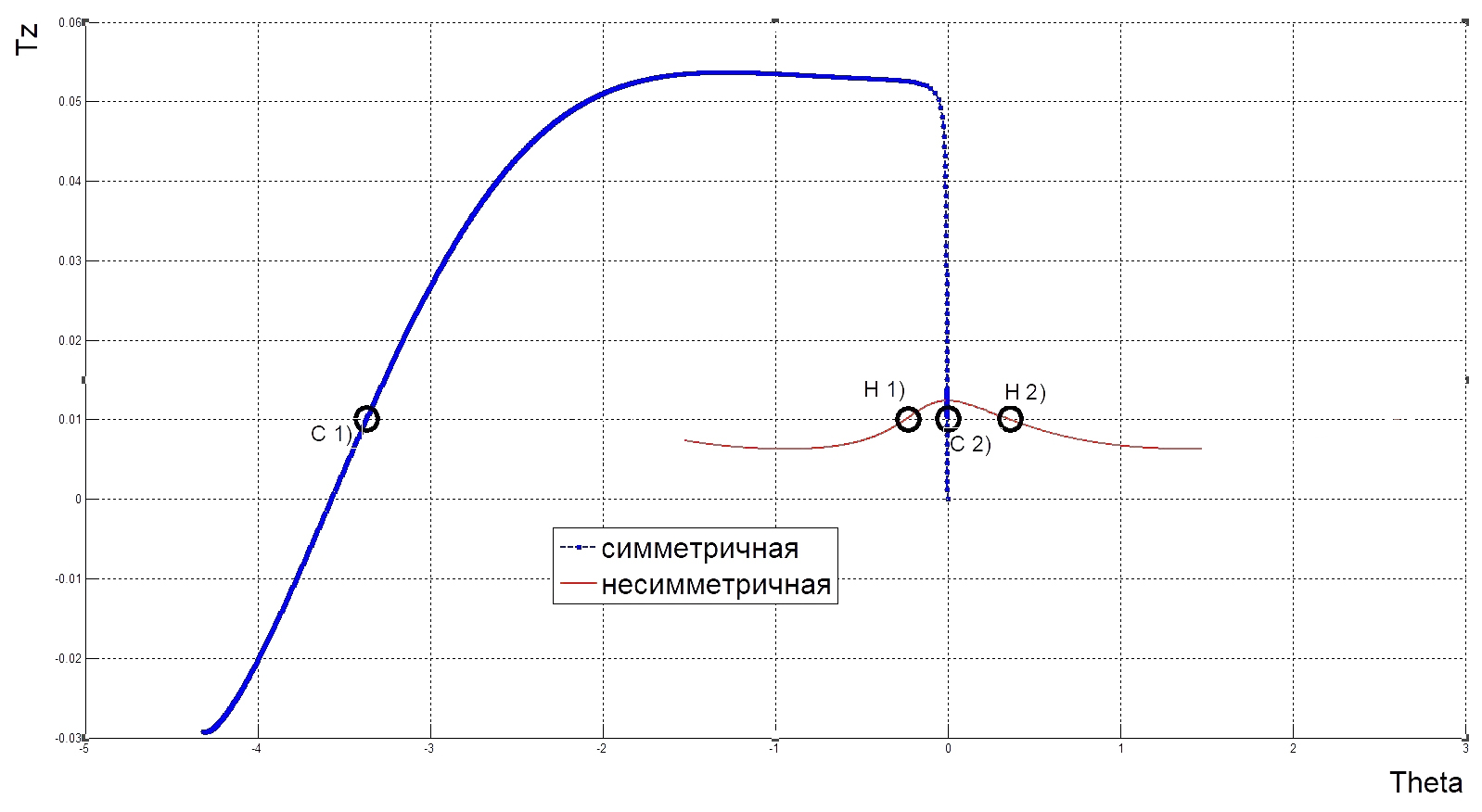

Зафиксируем 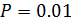и в точках пересечения с диаграммой (рис. 16) построим формы амортизатора (рис. 17–18).

Точка С 1)

Точка С 2)

Рис. 17. Формы симметричного варианта

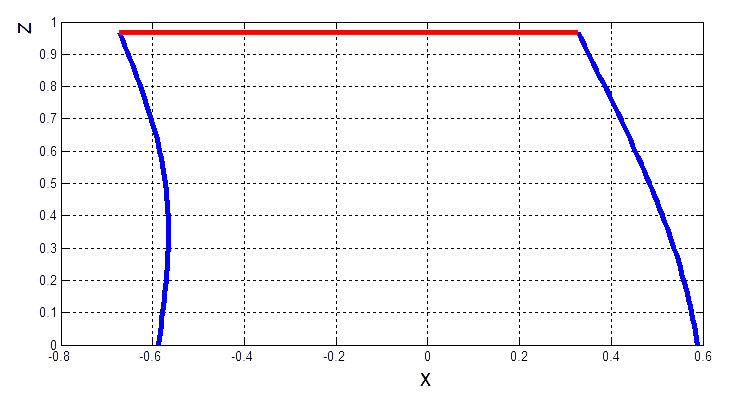
Точка Н 1)

Точка Н 2)

Рис. 18. Формы несимметричного варианта

Также, было выяснено, что при данных расчетных параметрах амортизатора бифуркация имеет место быть при 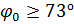. То есть, при 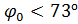будет реализовываться симметричный вариант.

Изолированное решение

Помимо бифуркации, методом деидеализациии было найдено изолированное решение.

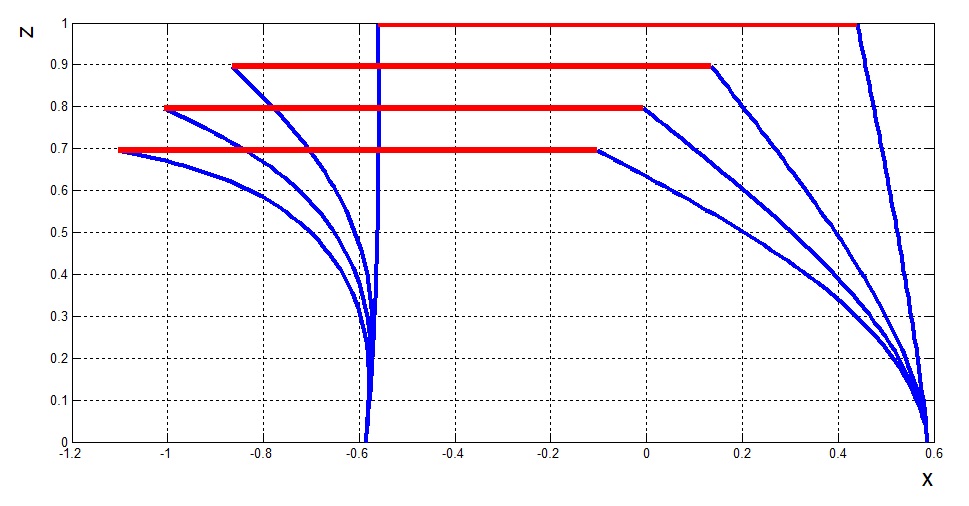
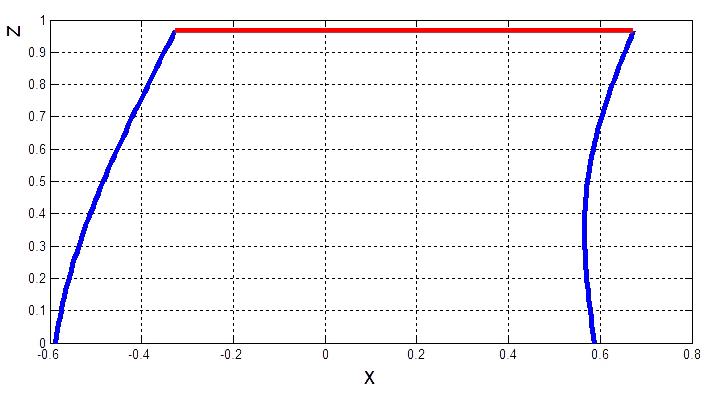
Рис. 19. Амортизатор в плоскости 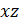, симметричное сжатие

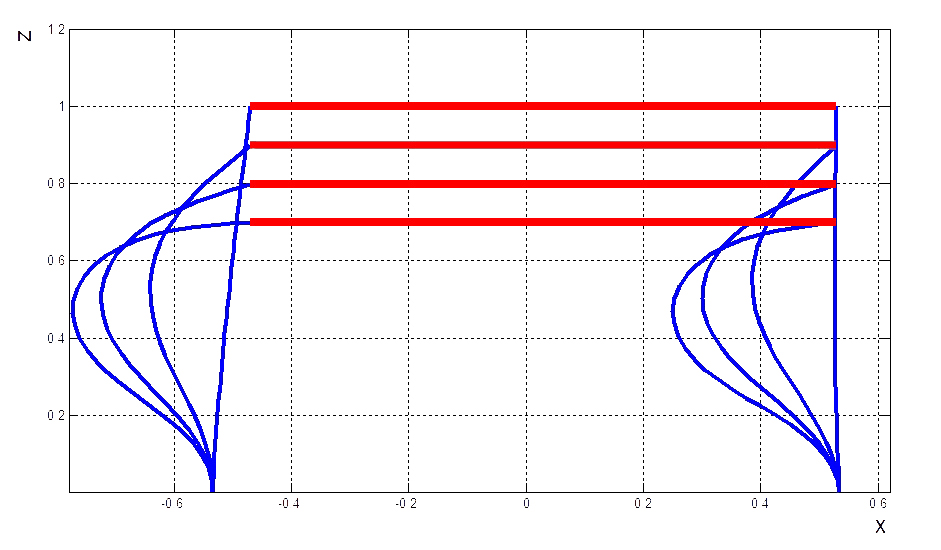
Рис. 20. Амортизатор в плоскости , несимметричное сжатие

Рассмотрим сжатие амортизатора с начальным углом наклона боковых пластин к оси , равному 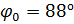(рис. 19–20).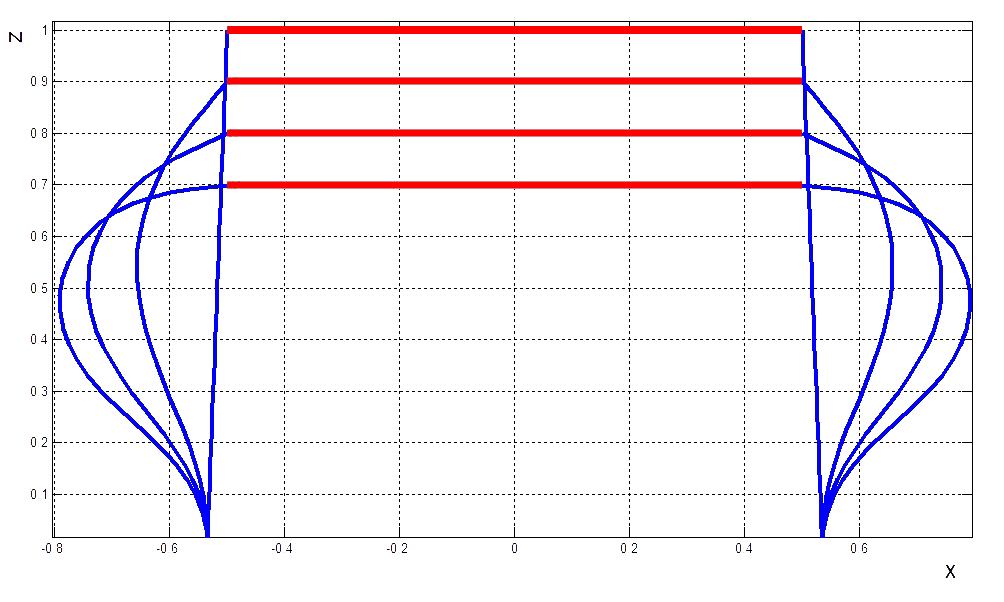

Рис. 21. Диаграмма нагрузка-перемещение

P

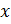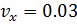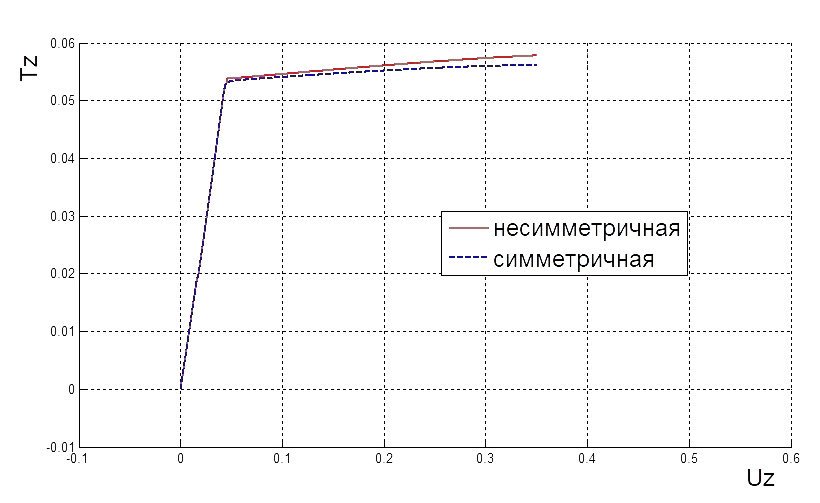
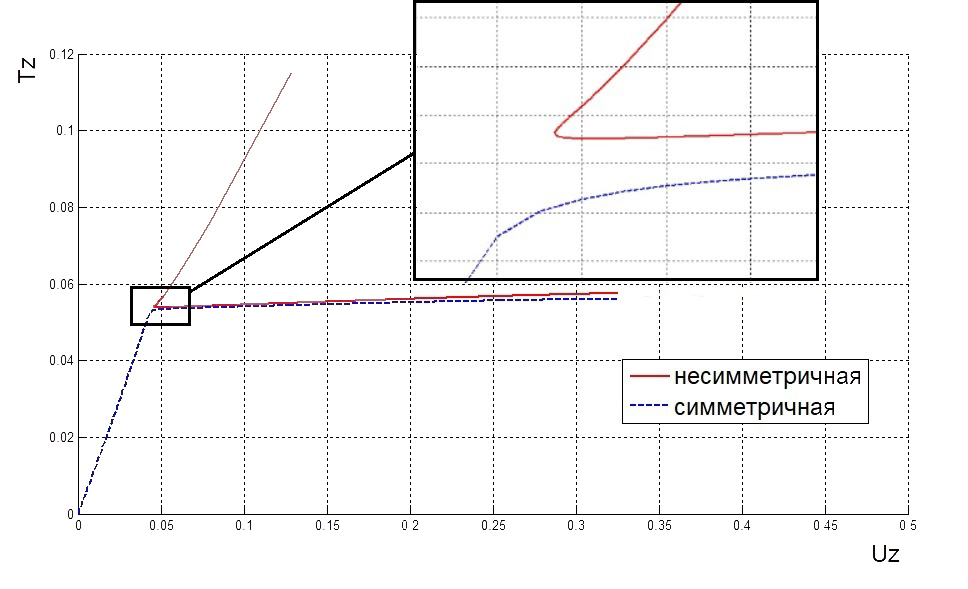
На рисунке 20 продемонстрирована несимметричная деформация, полученная немного иным путем, чем в главе 3.2: верхней пластине дается фиксированное смещение по оси , обозначим его . Далее все происходит аналогично главе 3.2.

Из рисунка 21 видно, что в точке 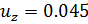графики нагрузки-перемещения для симметричной и для несимметричной форм сливаются в один. Рассмотрим окрестность этой точки ближе (рис. 22).

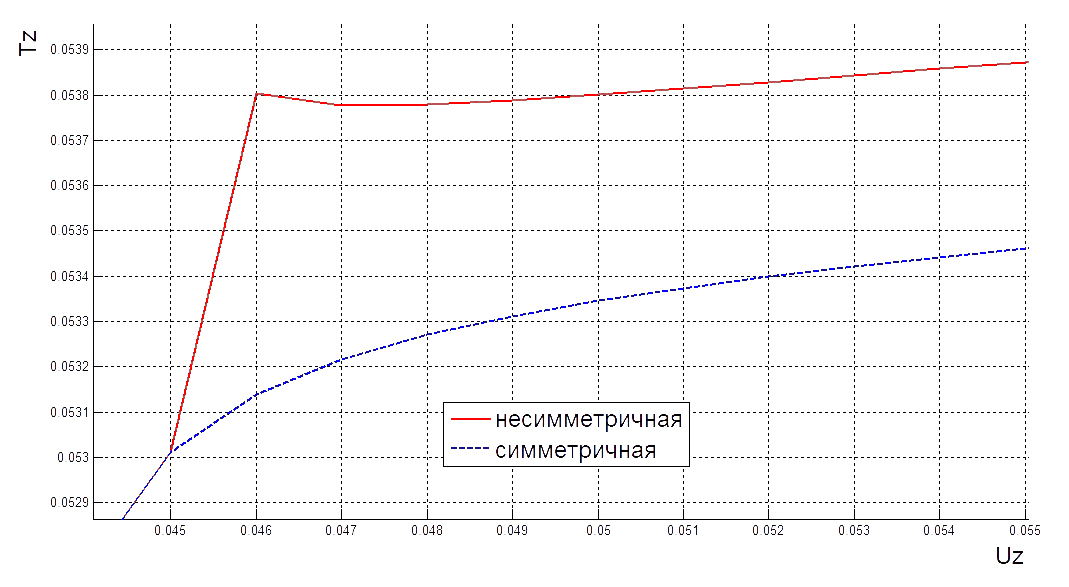
Рис. 22. Диаграмма нагрузка-перемещение

P

На рисунке 22 шаг параметра 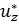равен 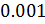. Видно, что нагрузка убывает, потом снова возрастает и на промежутке 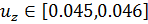осуществляется численный перескок с несимметричной ветви на симметричную. В этом промежутке сходимость ухудшается, поэтому требуется поменять параметр продолжения решения.

Если в окрестности точки перескока пройти по параметру 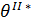– параметру угла поворота, то получается изолированное решение, изображенное на рисунке 23. Реализовываться этот вариант, скорее всего, не будет, тем более, симметричный вариант в этом случае выгоднее несимметричного по нагрузке.

Рис. 23. Диаграмма нагрузка-перемещение

P

Выводы

Составлен алгоритм решения нелинейной краевой задачи методом стрельбы в сочетании с методом продолжения по параметру. Написана программа, реализующая этот алгоритм. Отладка программы проводилась на примерах, известных из литературы.

Была рассмотрена задача деформации мостичного амортизатора при условии шарнирного опирания у верхнего основания и заделки у нижнего основания. Также, предполагалось, что основания при сжатии остаются параллельными, но верхнее основание может перемещаться по горизонтали. Задача в такой постановке другими авторами не рассматривалась.

Найдены бифуркационные ветви перехода от симметричного деформирования к несимметричному. Показано, при каком значении начального угла будет возможна бифуркация при расчетных параметрах.

В развитие работы можно рассмотреть другие толщины резиновых пластин; поставить условие возможности поворота верхнего основания при шарнирном опирании; рассмотреть криволинейные формы резиновых пластин.

Заключение

В ходе выполнения была написана программа, реализующая решение поставленной задачи. Найдены ветви потери устойчивости амортизатора и диапазон угла, при котором она реализуется для заданных расчетных параметров.

Список литературы

1. Бочкарева Н.Л., Колпак Е.П. Об устойчивости арочного амортизатора // Вестник СПбГУ, 1993. Сер. 1, вып. 4. С. 49–53.

2. Колпак Е.П. Устойчивость мостичного амортизатора из резиноподбного материала // Теория и методы расчета нелинейных пластин и оболочек, 1981. С.: Изд-во Саратовского ун-та, 1981. С. 43–45.

3. Черных К.Ф. Нелинейная теория упругости в машиностроительных расчетах. Л.: Машиностроение, 1986. 336 с.

4. Кабриц С.А., Михайловский Е.И., Товстик П.Е., Черных К.Ф., Шамина В.А. Общая нелинейная теория упругих оболочек. СПб.: СПбГУ, 2002. 386 с.

5. Kabrits S.A., Kolpak E.P. Finding bifurcation branches in nonlinear problems of statics of shells numerically, 2015 International conference «Stability and Control processes» in Memory of Zubov V.I., 2015. P. 389–391.

6. Kabrits S.A., Kolpak E.P. Numerical Study of Convergence of Nonlinear Models of the Theory of Shells with Thickness Decrease, AIP Conference Proceedings, 2016. Vol. 1738, №160006.

7. Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). М.: Наука, 1975. 631 с.

8. Кабриц С.А., Терентьев В.Ф. О численном построении диаграмм нагрузка-перемещение в одномерных нелинейных задачах теории стержней и оболочек // Актуальные проблемы нелинейной механики сплошных сред, 1977. Вып. 1. С. 155–171.

9. Алфутов Н.А. Основы расчета на устойчивость упругих систем. М.: Машиностроение, 1978. 312 с.

10. Пановко Я.Г., Губанова И.И. Устойчивость и колебания упругих систем. М.: Наука, 1987. 352 с.

11. Белкин А.Е., Семенов В.В., Семенов В.К. Численный анализ больших плоский деформаций арочного амортизатора // Вестник МГТУ им. Н.Э. Баумана, 2011. №2. С. 55–64.

12. Белкин А.Е., Хоминич Д.С. Расчет больших деформаций арочного амортизатора с учетом объемной сжимаемости резины // Вестник МГТУ им. Н.Э. Баумана, 2012. №2. С. 3–11.

Приложение

Краткое описание всех функций:

main –скрипт, запускающий работу программы;

BALKAM – функция, осуществляющая продолжения по параметру (сжатие амортизатора, несимметричный случай);

BALKAM1 – функция, осуществляющая продолжения по параметру (сжатие амортизатора, несимметричный случай);

PSI1 / PSI2 – функция от вектора начального приближения, задающая начальные условия для задачи Коши для правой / левой половинки (1.3);

PSI / PSITh – функция от вектора начального приближения, задающая граничные условия на верхнем основании при параметре продолжения решения вертикального перемещения / угла поворота (1.3);

FRESHE – функция от функции PSI1/PSI2и вектора начального приближения для вычисления невязки и матрицы Якоби в методе Ньютона;

PSI_PRINT1 / PSI_PRINT2 –функция от вектора деформации, осуществляющая построение формы правой / левой половинки амортизатора;

Runge –модуль метода Рунге – Кутты – Мерсона для системы дифференциальных уравнений (1.1);

solve_lambda –функция, вычисляющая методом касательных кратность удлинения срединной линии резиновых пластин амортизатора;

RVO –функция задания начальной геометрии и констант материала;

kgx –функция от вектора начального приближения, вычисляющая правые части системы дифференциальных уравнений (1.1).

function [g] = kgx(s,y)

%вычисление правых частей системы дифференциальных уравнений

% y[1]=v y[2]=u y[3]=Theta y[4]=M y[5]=Tx y[6]=Tz L1=lambda1

global lg

lg = 1;

[ R0,Z0,F0,K0,h0,mu,n,beta] = RVO(s);

fi=y(3)+F0; g=zeros(6,1);

Tn=y(5).*sin(fi)+y(6).*cos(fi);

Ts=y(5).*cos(fi)-y(6).*sin(fi);

lambda10=1;

lambda2=lg;

alfa=mu.*h0./n.*((1+beta)+(1-beta).*lambda2.^n);

L1=solve_lambda(Ts,lambda10,alfa,n,lambda2);

lambda3=1./(L1.*lambda2);

g(1)= L1.*cos(fi)-cos(F0);

g(2)=-L1.*sin(fi)+sin(F0);

b=(L1*lambda2)^n;

a=1/(L1.^2.*lambda2).*((1+beta)./b+(1-beta).*b);

kappa_s=6.*y(4)./(mu.*h0.^3)./a;

g(3)=L1.^2.*lambda2.*(kappa_s+K0)-K0;

g(4)=L1*Tn;

g(5)=0;

g(6)=0;

end

function [R0,Z0,F0,K0,h0,mu,n,beta] = RVO(s)

%начальная геометрия и константы материала

global ab

F0=85/180*pi;

R1=0.5; R0=R1+s.*cos(F0);

H=ab*sin(F0); Z0=H-s.*sin(F0);

K0=0;

h0=1/7;

mu=1;

n=2;

beta=1;

end

function [L1] = solve_lambda(T,L10,alfa,n,L2)

%вычисление кратности удлинения срединной линии резиновых пластин методом касательных

global lg

L1=L10; eps=1; b=L2.^(-n);

while eps>1E-10

a=L1.^(n-1); c=b./(a*L1*L1);

f=alfa.*(a-c)-T;

df=alfa.*((n-1)*a+(n+1).*c)/L1;

L11=L1-f/df;

eps=abs(L11-L1);

L1=L11;

lg = L11;

end

end

function [ Y ] = Runge(FT,TT0,TTK,TTH,EET,XX)

%Метод Рунге - Кутты - Мерсона с автоматическим шагом

T=TT0; C=abs(TTK-TT0)/3; NN=size(XX,1);

if C<=10^(-8)*abs(TTH)

return

end;

TTH=abs(TTH).*sign(TTK-TT0);

ib=1;

while (ib==1)

if (T+TTH-TTK)*sign(TTH)>0

TTH=TTK-T; ib=0;

end;

F0=FT(T,XX);

Y1=XX+F0.*TTH./3;

F1=FT(T+TTH./3,Y1); Y1=XX+(F0+F1).*TTH./6;

F2=FT(T+TTH/3,Y1); Y1=XX+(F0+3.*F2).*TTH./8;

F3=FT(T+TTH/2,Y1); Y1=XX+(F0-3.*F2+4.*F3).*TTH./2;

F1=FT(T+TTH,Y1);

Y1=abs(F0-4.5.*F2+4.*F3-0.5.*F1).*C;

II=0; JJ=0;

for I=1:NN

if EET(I)~=0

II=II+1;

if Y1(I) >= EET(I)*5

TTH=TTH./2;

continue;

else

if Y1(I)<= EET(I)/32

JJ=JJ+1;

end

end

end

end

T=T+TTH;

XX=XX+(F0+4.*F3+F1).*TTH./6;

if (II~=0) && (II==JJ)

TTH=2.*TTH;

end

if abs(T-TTK)>1.E-6.*C

continue

end

end

Y=XX;

end

function [Y] = PSI_PRINT1(X)

%построение формы правой пластинки амортизатора

global ab shag dlt ln

Z=zeros(6,1);

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(0);

Z(1)=0; %начальные условия

Z(2)=0;

Z(3)=0;

Z(4)=X(1);

Z(5)=X(2);

Z(6)=X(3);

Ep=zeros(6,1);

m=50;

YY=zeros(m,6);

x=linspace(ab,0,m);

for i=1:m-1

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(x(i));

if i==1

YY(i,1)=R0+Z(1);

YY(i,2)=Z0+Z(2);

end

ZZ=Runge(@kgx,x(i),x(i+1),shag,Ep,Z);

Z=ZZ;

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(x(i+1));

YY(i+1,1)=R0+Z(1);

YY(i+1,2)=Z0+Z(2);

end

ln(1) = R0+Z(1);

ln(2) = Z0+Z(2);

hold on; grid on;

if (dlt<0)

subplot(2,2,1);

plot(YY(:,1),YY(:,2),'LineWidth',4);

else

subplot(2,2,2);

plot(YY(:,1),YY(:,2));

end

hold on; grid on;

end

function [Y] = PSI_PRINT2(X)

%построение формы левой пластинки амортизатора

global ab shag dlt ln

Z=zeros(6,1);

[ R0,Z0,F0,K0,h0,mu,n,beta] = RVO(0);

Z(1)=0; %начальные условия

Z(2)=0;

Z(3)=0;

Z(4)=X(4);

Z(5)=X(5);

Z(6)=X(6);

Ep=zeros(6,1);

m=50;

YY=zeros(m,6);

DD1=zeros(m,6);

DD2=zeros(m,6);

YY1=zeros(m,6);

x=linspace(ab,0,m);

for i=1:m-1

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(x(i));

if i==1

YY(i,1)=-R0-Z(1);

YY(i,2)=Z0+Z(2);

end

ZZ=Runge(@kgx,x(i),x(i+1),shag,Ep,Z);

Z=ZZ;

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(x(i+1));

YY(i+1,1)=-R0-Z(1);

YY(i+1,2)=Z0+Z(2);

end

ln(3) = -R0-Z(1);

ln(4) = Z0+Z(2);

hold on; grid on;

if (dlt<0)

subplot(2,2,1);

plot(YY(:,1),YY(:,2),'LineWidth',4);

else

subplot(2,2,2);

plot(YY(:,1),YY(:,2));

end

hold on; grid on;

end

function [Y, DF] = FRESHE(PSI,X);

%вычисление Y=F(x) (невязка) и DF (матрица якоби dPSI/dx)

nfresh=size(X,1);

Y=PSI(X); %вектор деформации

for k=1:nfresh

A=X(k); P=A*1.E-4;

if abs(P)<1.E-8

P=1.E-8;

end

X(k)=A+P;

Z=PSI(X);

X(k)=A;

for j=1:nfresh

DF(j,k)=(Z(j)-Y(j))./P;

end

end

end

function [ZZ] = PSI1(X)

%начальные условия для решения задачи коши правой половинки

global ab shag

Z=zeros(6,1);

Z(1)=0;

Z(2)=0;

Z(3)=0;

Z(4)=X(1);

Z(5)=X(2);

Z(6)=X(3);

Ep=zeros(6,1);

ZZ=Runge(@kgx,ab,0,shag,Ep,Z); %решение задачи коши

end

function [ZZ] = PSI2(X)

%начальные условия для решения задачи коши левой половинки

global ab shag

Z=zeros(6,1);

Z(1)=0;

Z(2)=0;

Z(3)=0;

Z(4)=X(4);

Z(5)=X(5);

Z(6)=X(6);

Ep=zeros(6,1);

ZZ=Runge(@kgx,ab,0,shag,Ep,Z); %решение задачи коши

end

function [Y] = PSI(X)

% граничные условия на верхнем основании при параметре продолжения вертикального перемещения

global delta ab shag deltax

Z1 = PSI1(X); %правая половинка

Z2 = PSI2(X); % левая половинка

Y(1) = Z1(4); %граничные условия

Y(2) = Z2(4);

Y(3) = Z1(1) + Z2(1);

Y(4) = Z1(2) - Z2(2);

Y(5) = Z2(5) - Z1(5) + deltax;

Y(6) = Z1(2) - delta;

end

function [Y] = PSITh(X)

% граничные условия на верхнем основании при параметре продолжения угла поворота правой пластинке

global tzz

Z1 = PSI1(X);

Z2 = PSI2(X);

Y(1) = Z1(4); Y(2) = Z2(4);

Y(3) = Z1(1) + Z2(1);

Y(4) = Z1(2) - Z2(2);

Y(5) = Z2(5) - Z1(5);

Y(6) = Z2(3) - tzz;

end

function [] = BALKAM

%функция, осуществляющая продолжения по параметру (сжатие амортизатора, несимметричный случай)

global q1 obrshag mas lnln p1 tzz distance TzL TzR grdlt delta ab dlt shag deltax ln t ogr

ln = zeros(4);

lnln = [];

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(0);

nfresh=3; %размерность

ab=1; %длина боковых пластин

shag=0.05; %шаг интегрирования

kol = 6; %размерность вектора системы дифференциальных уравнений

X=zeros(kol,1);

Xp=zeros(kol,1);

X0=zeros(kol,1);

X1=zeros(kol,1);

q1 = 1;

mas = []; %массив данных

TzL = [];

TzR = [];

Tz = [];

grdlt = []; %вектор параметров

rr = 0;

er = 0;

ch = 0; %счетчик

while (abs(delta)<(ab*sin(F0)-abs(dlt))) && (ogr-abs(dlt)>abs(delta))&& (q1~=0); %цикл сжатия

iter=0; %счетчик

s=1; %параметр сходимости

Xp = X;

rrr = 0;

if (er~=1)

delta = delta+dlt; %продолжение по параметру

end

if (delta<distance) %проверка, дошел ли процесс до заданного параметра и последующий разворот назад

deltax = 0;

dlt = -dlt/obrshag;

rrr = 1;

rr = 1;

end;

if (rr == 1) && (delta>-p1-0.0000001) && (delta<-p1+0.0000001) %условие смена параметра

er = 1;

end;

if (delta>-p1-0.0000001) && (er == 1) && (delta<-p1+0.0000001) %смена параметра

ll = length(Tz);

thxR = (Tz(ll)-Tz(ll-1))/100;

thxRR = thxR;

thetaxR = Tz(ll);

end;

if (er == 1) && (rr == 1) && (delta>-0.007) %обратная смена параметра при успешном проходе

er = 0;

end;

if (delta>-dlt+dlt/10) && (dlt>0) %условие остановки алгоритма

q1 = 0;

end;

if (er == 1) && (delta<-0.007) %экстраполяция параметра

tzz = thetaxR + thxR;

thxR = thxR +thxRR;

end;

while s>0.0001 %цикл сжатия

iter=iter+1;

if (er == 1) && (delta<-0.007) %определение параметра

if s>0.1 %условие сходимости

[Y,DF]=FRESHE(@PSITh,X); %вычисление правых частей

else [Y]=PSITh(X); %вычисление правых частей

end

else

if s>0.1

[Y,DF]=FRESHE(@PSI,X);

else [Y]=PSI(X);

end

end

WW=DF\Y'; %решение системы нелинейных уравнений

X=X-WW; %вектор деформации

s=0;

for i=1:nfresh %сходимость

s=s+abs(WW(i))./(abs(X(i))+1e-10);

end

end

if (er == 1) && (delta<-0.007) %вычисление параметра вертикального смещения при движении по другому

zzz = PSI2(X);

delta = zzz(2);

end;

if (dlt>0)

zzz = PSI2(X); %вектор левой половинки

z11 = PSI1(X); %вектор правой половинки

z22 = PSI2(X);

uzz = z11(6) + z22(6); %вертикальная суммарная нагрузка

mas = [mas;[-delta,iter,uzz,z11',z22',X']]; %вектор данных

TzR=[TzR,X(3)]; %вектор нагрузки правой половинки

TzL=[TzL,X(6)]; %вектор нагрузки левой половинки

Tz = [Tz,zzz(3)]; %вектор параметра угла поворота

grdlt = [grdlt,-delta]; %вектор параметра вертикального смещения

end

t = 1;

PSI_PRINT1(X); %построение формы правой половинки

PSI_PRINT2(X); %построение формы левой половинки

hold on; grid on;

if (dlt<0) %постоение верхней пластины

subplot(2,2,1)

plot([ln(1),ln(3)],[ln(2),ln(4)],'r');

else

lnln = [lnln;[ln(1),ln(3),ln(2),ln(4)]];

end

hold on; grid on;

[delta,iter]

X1 = X;

X = (X-X0).*(-2*dlt)./(-dlt+(1e-20)) + X0; %экстраполяция начального приближения методом касательных

X0 = X1;

ch = ch + 1;

end

hold on; grid on;

subplot(2,2,2);

for i=1:length(lnln)

plot([lnln(i,1),lnln(i,2)],[lnln(i,3),lnln(i,4)],'r'); %постоение верхней пластины

end;

hold on; grid on;

end

function [] = BALKAM1

%функция, осуществляющая продолжения по параметру (сжатие амортизатора, симметричный случай)

global q1 ii mas1 razb ThetaS distance TzL1 TzR1 grdlt1 delta ab dlt shag ln t ogr

ln = zeros(4);

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(0);

nfresh=3;

ab=1;

shag=0.05;

kol = 6;

X=zeros(kol,1);

Xp=zeros(kol,1);

X0=zeros(kol,1);

X1=zeros(kol,1);

q1 = 1;

mas1 = [];

TzL1 = [];

TzR1 = [];

ThetaS = [];

grdlt1 = [];

ii = 1;

while (abs(delta)<(ab*sin(F0)-abs(dlt))) && (ogr-abs(dlt)>abs(delta)) && (q1~=0) && (distance<delta)

iter=0; s=1;

Xp = X;

rrr = 0;

delta = delta+dlt;

if (delta>-0.0080001) && (delta<-0.0079999)

dlt = dlt/razb;

end;

if (delta>-0.01200001) && (delta<-0.01199999)

dlt = dlt*razb;

end;

while s>0.0001

iter=iter+1;

if s>0.1

[Y,DF]=FRESHE(@PSI,X);

else [Y]=PSI(X);

end

WW=DF\Y';

X=X-WW;

s=0;

for i=1:nfresh

s=s+abs(WW(i))./(abs(X(i))+1e-10);

end

end

TzR1=[TzR1,X(3)];

TzL1=[TzL1,X(6)];

grdlt1 = [grdlt1,-delta];

ThetaS = [ThetaS,X(1)];

t = 1;

if (X(3)+X(6) > 0.0099) && (X(3)+X(6) < 0.011)

PSI_PRINT1(X);

PSI_PRINT2(X);

end;

[delta,iter]

z11 = PSI1(X);

z22 = PSI2(X);

uzz = z11(6) + z22(6);

mas1 = [mas1;[-delta,iter,uzz,z22',X']];

X1 = X;

X = (X-X0).*(-2*dlt)./(-dlt+(1e-20)) + X0;

X0 = X1;

end

%main

%скрипт, запускающий работу программы

global delta distance1 razb p1 ln mas mas1 lnln ii arr1 arr ThetaS obrshag distance grdlt TzL TzR grdlt1 TzL1 TzR1 ab ThetaL ThetaR dlt deltax ogr

hold off;

[R0,Z0,F0,K0,h0,mu,n,beta] = RVO(0);

dlt = -0.001; %задание шага параметра продолжения

deltax = 0.001; %задание неидеальности

p1 = 0.011; %точка при достижении которой осуществляется смена параметра

obrshag = 1; %разбиение шага при движении обратно

distance = -0.4; %точка предела сжатия

razb = 10; %разбиение шага при движении по другому параметру

delta = -dlt; %начальное значение параметра (обнулится при заходе в цикл)

ogr = ab*sin(F0)+3*dlt; %ограничение для того, чтобы верхняя пластина не перерезала нижнюю

BALKAM; %основная функция несимметричного сжатия

hold on; grid on;

Tt = TzL + TzR; %вектор суммарной вертикальной нагрузки

% yy = [];

% yy=[yy;[grdlt;Tt]];

% hold on; grid on;

subplot(2,2,4); %диаграмма нагрузка-перемещение для правой и левой половинок по отдельности

hold on; grid on;

plot(grdlt, TzL,'r');

plot(grdlt, TzR,'b');

legend('левая','правая',0);

plot(grdlt, TzL,'r*',grdlt, TzR,'*');

ylabel('Tz');

xlabel('delta');

hold on; grid on;

deltax = 0; %обнуление неидеальности

distance = -ogr;

dlt = -0.001;

delta = -dlt;

BALKAM1; %основная функция симметричного сжатия

hold on; grid on; %построение диаграммы нагрузка-перемещения для несиммеричного варианта

subplot(2,2,3);

Tt = TzL + TzR;

plot(grdlt, Tt,'r','LineWidth',2);

%plot(grdlt, Tt,'r*');

ylabel('Tz');

xlabel('Uz');

%yy = [];

%yy=[yy;[grdlt;Tt]];

hold on; grid on;

Tt = TzL1 + TzR1;

plot(grdlt1, Tt,'--b','LineWidth',2); %построение диаграммы нагрузка-перемещение для симметричного варианта

legend('несимметричная','симметричная',0);

%plot(grdlt, Tt,'b*');

hold on; grid on;

Кафедра вычислительных методов механики деформируемого тела

Горх Эдуард Владимирович