Однородная цилиндрическая стенка

Однослойная плоская стенка

Имеется однородная плоская стенка с коэффициентом теплопроводности л и толщиной д. По одну сторону стенки находится горячая среда с температурой по другую - холодная с температурой t_ж2. Температуры поверхностей стенки неизвестны, обозначим их буквами t_с1 и t_с2 (рис. 6-2). Задано значение суммарного коэффициента теплоотдачи на горячей стороне б₁ на холодной - б₂.

При установившемся тепловом состоянии количество теплоты, переданное от горячей жидкости к стенке, равно количеству теплоты, переданному через стенку, и количеству теплоты, отданному от стенки к холодной жидкости. Следовательно, для плотности теплового потока q можно написать три выражения:

Из этих уравнений определяются частные температурные на поры, а именно:

Складывая их, получаем полный температурный напор:

из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи

Таким образом, чтобы вычислить значение коэффициента теплопередачи k для плоской стенки, необходимо знать толщину этой стенки д, коэффициент теплопроводности л и значения коэффициентов теплоотдачи б₁ и б₂.

Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи. Из уравнения (6-5) эта величина равна:

Теплопередача через однослойную плоскую стенку; характер изменения температуры в теплоносителях и разделяющей их стенке

Из этого соотношения следует, что общее термическое сопротивление равно сумме частных:

где R_бl = 1/б₁ - частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя; R_л = д/л - частное термическое сопротивление теплопроводности (стенки); R_a2 = 1/б₂ - частное термическое сопротивление теплоотдачи со стороны холодного теплоносителя

Многослойная плоская стенка

Рассматривается стенка, состоящая из нескольких, например двух, слоев (рис. 6-3). Толщины слоев д₁ и д₂, коэффициенты теплопроводности л₁ и л₂. С одной стороны находится горячая среда с температурой t_ж1 с другой - холодная с температурой t_ж2. Значение суммарного коэффициента теплоотдачи с горячей стороны б₁ с холодной б₂.

При установившемся тепловом состоянии системы плотность теплового потока постоянна и поэтому можно написать:

Из этих уравнений определяются частные температурные напоры:

Складывая раздельно левые и правые части уравнений, получаем полный температурный напор

из которого определяется значение плотности теплового потока 1

и значение коэффициента теплопередачи для двухслойной плоской стенки

Распределение температур при теплопередаче через плоскую одно- и многослойную стенки представлено соответственно на рис. 6-2 и 6-3.

Неизвестные температуры могут быть определены из уравнений (е):

Если стенка состоит из нескольких слоев толщиной д₁, д₂., д_n и коэффициенты теплопроводности их соответственно л_1, л₂,…, л_n, то общее термическое сопротивление теплопередачи будет равно:

В этом случае уравнение (6-5) принимает вид:

Теплопередача через многослойную плоскую стенку

Температуры стенки можно определить и графически. Один из таких способов был описан в гл. 1. Поэтому мы здесь рассмотрим второй, который основан на замене термического сопротивления горячей и холодной среды термическим сопротивлением твердой стенки с таким же коэффициентом теплопроводности, как и действительная стенка.

Пусть температуры наружных поверхностей воображаемой стенки соответственно равны температурам горячей и холодной среды t_ж1 и t_ж2 (рис. 6-4). Количество передаваемой теплоты остается без изменения. Тогда общая толщина Д этой воображаемой стенки определяется из соотношения

откуда

Здесь величины л/а₁ и л/б₂ имеют размерность длины, м, они определяют собой эквивалентные толщины. При графическом построении сначала строится реальная стенка толщиной д (в любом масштабе), затем по одну сторону от нее в том же масштабе откладывается значение л/б₁ а по другую - значение л/б₂. Из крайних точек а и bпо вертикали в некотором масштабе откладываются значения температур t_ж1 и t_ж2. Полученные точки А и С соединяются прямой линией. Точки пересечения этой прямой с поверхностями действительной стенки дают значения искомых температур t_с1 и t_с2.

Действительно, из подобия треугольников АBС и АВЕ имеем, что DЕ/ВС = АD/АВ, откуда

Согласно уравнению (б)

следовательно, отрезок МЕ=МD-ЕD = t_ж1 - (t_Ж1 - t_c1) = t_c1. Таким же путем можно показать, что отрезок NG в выбранном масштабе температуры равен t_с2.

Если стенка многослойная и требуется определить лишь температуру наружных поверхностей, то построение производят точно таким же образом, как и для однослойной стенки, имея дело лишь со средним коэффициентом теплопроводности многослойной стенки. Температура же между слоями в точке А определяется по пересечению двух лучей.

Для многослойной плоской стенки полное термическое сопротивление будет определяться по следующей формуле: R0 = (1/a1 + d1/l1 + d2/l2 + … + dn/ln +1/a2), (12.7) а коэффициент теплопередачи: К = 1 / (1/a1 + d1/l1 + d2/l2 + … + dn/ln +1/a2), (12.8)
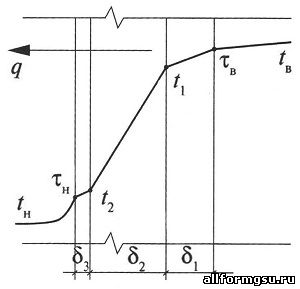
Если с одной стороны многослойной стенки, состоящей из n слоев, поддерживается температура tв, а с другой стороны tн< tв, то возникает тепловой поток q, Вт/м² (Рис.6).
Этот тепловой поток движется от среды с температурой tв, ºС, к среде с температурой tн, ºС, проходя последовательно от внутренней среды к внутренней поверхности с температурой τв, ºС:
q= (1/ Rв). (tв - τв), (2.17)

затем от внутренней поверхности сквозь первый слой с термическим сопротивлением R Т,1 к стыку первого и второго слоев:
q= (1/ RТ,1). (τв - t1), (2.18)
после этого через все остальные слои
q= (1/ R Т, i). (ti-1 - ti), (2.19)
и, наконец, от наружной поверхности с температурой τн к наружной среде с температурой tн:
q= (1/ R н). (τн - tн), (2.20)
где R Т, i- термическое сопротивление слоя с номером i, м². ºС/Вт;
Rв, Rн - сопротивления теплообмену на внутренней и наружной поверхностях, м². ºС/Вт;
ti-1 - температура, ºС, на стыке слоев с номерами i-1 и i;
ti - температура, ºС, на стыке слоев с номерами i и i+1.

Переписав (2.16) - (2.19) относительно разностей температуры и сложив их, получим равенство:
tв - tн = q. (Rв+RТ,1+RТ,2+…+RТ,i+….+RТ,n+Rн) (2.21)
Выражение в скобках - сумма термических сопротивлений плоскопараллельных последовательно расположенных по ходу теплового потока слоев ограждения и сопротивлений теплообмену на его поверхностях называется общим сопротивлением теплопередаче ограждения Ro, м². ºС/Вт:
Ro=Rв+ΣRТ,i+Rн, (2.22)
а сумма термических сопротивлений отдельных слоев ограждения - его термическим сопротивлением RТ, м².ºС/Вт:
RТ = RТ,1+RТ,2+…+Rв. п+…. +R Т,n, (2.23)
где R Т,1, R Т,2,…, R Т,n - термические сопротивления отдельных плоскопараллельных последовательно расположенных по ходу теплового потока слоев слоев ограждающей конструкции, м². ºС/Вт, определяемые по формуле (2.4);
Rв. п - термическое сопротивление замкнутой воздушной прослойки, м². ºС/Вт, по п.2.1.4
По физическому смыслу общее сопротивление теплопередаче ограждения Ro - это разность температуры сред по разные стороны ограждения, которая формирует проходящий через него тепловой поток плотностью 1 Вт/ м², в то время как термическое сопротивление многослойной конструкции - разность температуры наружной и внутренней поверхностей ограждения, которая формирует проходящий через него тепловой поток плотностью 1 Вт/ м²,Из (2.22) следует, что тепловой поток q, Вт/м², проходящий через ограждение, пропорционален разности температуры сред по разные стороны ограждения (tв - tн) и обратно пропорционален общему сопротивлению теплопередаче Ro
q= (1/ Rо). (tв - tн), (2.24)

Вопрос №7

Однослойная плоская стенка

Имеется однородная плоская стенка с коэффициентом теплопроводности л и толщиной д. По одну сторону стенки находится горячая среда с температурой по другую - холодная с температурой t_ж2. Температуры поверхностей стенки неизвестны, обозначим их буквами t_с1 и t_с2 (рис. 6-2). Задано значение суммарного коэффициента теплоотдачи на горячей стороне б₁ на холодной - б₂.

При установившемся тепловом состоянии количество теплоты, переданное от горячей жидкости к стенке, равно количеству теплоты, переданному через стенку, и количеству теплоты, отданному от стенки к холодной жидкости. Следовательно, для плотности теплового потока q можно написать три выражения:

Из этих уравнений определяются частные температурные на поры, а именно:

Складывая их, получаем полный температурный напор:

из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи

Таким образом, чтобы вычислить значение коэффициента теплопередачи k для плоской стенки, необходимо знать толщину этой стенки д, коэффициент теплопроводности л и значения коэффициентов теплоотдачи б₁ и б₂.

Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи. Из уравнения (6-5) эта величина равна:

Теплопередача через однослойную плоскую стенку; характер изменения температуры в теплоносителях и разделяющей их стенке

Из этого соотношения следует, что общее термическое сопротивление равно сумме частных:

где R_бl = 1/б₁ - частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя; R_л = д/л - частное термическое сопротивление теплопроводности (стенки); R_a2 = 1/б₂ - частное термическое сопротивление теплоотдачи со стороны холодного теплоносителя

Многослойная плоская стенка

Рассматривается стенка, состоящая из нескольких, например двух, слоев (рис. 6-3). Толщины слоев д₁ и д₂, коэффициенты теплопроводности л₁ и л₂. С одной стороны находится горячая среда с температурой t_ж1 с другой - холодная с температурой t_ж2. Значение суммарного коэффициента теплоотдачи с горячей стороны б₁ с холодной б₂.

При установившемся тепловом состоянии системы плотность теплового потока постоянна и поэтому можно написать:

Из этих уравнений определяются частные температурные напоры:

Складывая раздельно левые и правые части уравнений, получаем полный температурный напор

из которого определяется значение плотности теплового потока 1

и значение коэффициента теплопередачи для двухслойной плоской стенки

Распределение температур при теплопередаче через плоскую одно- и многослойную стенки представлено соответственно на рис. 6-2 и 6-3.

Неизвестные температуры могут быть определены из уравнений (е):

Если стенка состоит из нескольких слоев толщиной д₁, д₂., д_n и коэффициенты теплопроводности их соответственно л_1, л₂,…, л_n, то общее термическое сопротивление теплопередачи будет равно:

В этом случае уравнение (6-5) принимает вид:

Теплопередача через многослойную плоскую стенку

Температуры стенки можно определить и графически. Один из таких способов был описан в гл. 1. Поэтому мы здесь рассмотрим второй, который основан на замене термического сопротивления горячей и холодной среды термическим сопротивлением твердой стенки с таким же коэффициентом теплопроводности, как и действительная стенка.

Пусть температуры наружных поверхностей воображаемой стенки соответственно равны температурам горячей и холодной среды t_ж1 и t_ж2 (рис. 6-4). Количество передаваемой теплоты остается без изменения. Тогда общая толщина Д этой воображаемой стенки определяется из соотношения

откуда

Здесь величины л/а₁ и л/б₂ имеют размерность длины, м, они определяют собой эквивалентные толщины. При графическом построении сначала строится реальная стенка толщиной д (в любом масштабе), затем по одну сторону от нее в том же масштабе откладывается значение л/б₁ а по другую - значение л/б₂. Из крайних точек а и bпо вертикали в некотором масштабе откладываются значения температур t_ж1 и t_ж2. Полученные точки А и С соединяются прямой линией. Точки пересечения этой прямой с поверхностями действительной стенки дают значения искомых температур t_с1 и t_с2.

Действительно, из подобия треугольников АBС и АВЕ имеем, что DЕ/ВС = АD/АВ, откуда

Согласно уравнению (б)

следовательно, отрезок МЕ=МD-ЕD = t_ж1 - (t_Ж1 - t_c1) = t_c1. Таким же путем можно показать, что отрезок NG в выбранном масштабе температуры равен t_с2.

Если стенка многослойная и требуется определить лишь температуру наружных поверхностей, то построение производят точно таким же образом, как и для однослойной стенки, имея дело лишь со средним коэффициентом теплопроводности многослойной стенки. Температура же между слоями в точке А определяется по пересечению двух лучей.

Для многослойной плоской стенки полное термическое сопротивление будет определяться по следующей формуле: R0 = (1/a1 + d1/l1 + d2/l2 + … + dn/ln +1/a2), (12.7) а коэффициент теплопередачи: К = 1 / (1/a1 + d1/l1 + d2/l2 + … + dn/ln +1/a2), (12.8)
Если с одной стороны многослойной стенки, состоящей из n слоев, поддерживается температура tв, а с другой стороны tн< tв, то возникает тепловой поток q, Вт/м² (Рис.6).
Этот тепловой поток движется от среды с температурой tв, ºС, к среде с температурой tн, ºС, проходя последовательно от внутренней среды к внутренней поверхности с температурой τв, ºС:
q= (1/ Rв). (tв - τв), (2.17)

затем от внутренней поверхности сквозь первый слой с термическим сопротивлением R Т,1 к стыку первого и второго слоев:
q= (1/ RТ,1). (τв - t1), (2.18)
после этого через все остальные слои
q= (1/ R Т, i). (ti-1 - ti), (2.19)
и, наконец, от наружной поверхности с температурой τн к наружной среде с температурой tн:
q= (1/ R н). (τн - tн), (2.20)
где R Т, i- термическое сопротивление слоя с номером i, м². ºС/Вт;
Rв, Rн - сопротивления теплообмену на внутренней и наружной поверхностях, м². ºС/Вт;
ti-1 - температура, ºС, на стыке слоев с номерами i-1 и i;
ti - температура, ºС, на стыке слоев с номерами i и i+1.

Переписав (2.16) - (2.19) относительно разностей температуры и сложив их, получим равенство:
tв - tн = q. (Rв+RТ,1+RТ,2+…+RТ,i+….+RТ,n+Rн) (2.21)
Выражение в скобках - сумма термических сопротивлений плоскопараллельных последовательно расположенных по ходу теплового потока слоев ограждения и сопротивлений теплообмену на его поверхностях называется общим сопротивлением теплопередаче ограждения Ro, м². ºС/Вт:
Ro=Rв+ΣRТ,i+Rн, (2.22)
а сумма термических сопротивлений отдельных слоев ограждения - его термическим сопротивлением RТ, м².ºС/Вт:
RТ = RТ,1+RТ,2+…+Rв. п+…. +R Т,n, (2.23)
где R Т,1, R Т,2,…, R Т,n - термические сопротивления отдельных плоскопараллельных последовательно расположенных по ходу теплового потока слоев слоев ограждающей конструкции, м². ºС/Вт, определяемые по формуле (2.4);
Rв. п - термическое сопротивление замкнутой воздушной прослойки, м². ºС/Вт, по п.2.1.4
По физическому смыслу общее сопротивление теплопередаче ограждения Ro - это разность температуры сред по разные стороны ограждения, которая формирует проходящий через него тепловой поток плотностью 1 Вт/ м², в то время как термическое сопротивление многослойной конструкции - разность температуры наружной и внутренней поверхностей ограждения, которая формирует проходящий через него тепловой поток плотностью 1 Вт/ м²,Из (2.22) следует, что тепловой поток q, Вт/м², проходящий через ограждение, пропорционален разности температуры сред по разные стороны ограждения (tв - tн) и обратно пропорционален общему сопротивлению теплопередаче Ro
q= (1/ Rо). (tв - tн), (2.24)

Вопрос №7

Однородная цилиндрическая стенка

Пусть имеется цилиндрическая стенка (труба) с внутренним диаметром d_l внешним d₂ и длиной l. Стенка трубы однородна; ее коэффициент теплопроводности л. Внутри трубы горячая среда с температурой t_ж1, а снаружи - холодная с температурой t_ж2. Температуры поверхностей стенки неизвестны, обозначим их через t_cl и t_c2 (рис. 6-6). Со стороны горячей среды суммарный коэффициент теплоотдачи б₁, а со стороны холодной б₂.

При установившемся тепловом состоянии системы количество теплоты, отданное горячей и воспринятое холодной средой, одно и то же. Следовательно, можно написать:

Из этих соотношений определяем частные температурные напоры:

Складывая уравнения системы (к), получаем полный температурный напор

Из уравнения (л) определяется значение линейной плотности теплового потока q_l

откуда линейный коэффициент теплопередачи (на 1 м длины трубы)

Величина, обратная линейному коэффициенту теплопередачи, 1/k_l называется линейным термическим сопротивлением теплопередачи.

Из уравнения (6-9) имеем:

Последнее означает, что общее термическое сопротивление равно сумме частных - термического сопротивления теплопроводности стенки и термических сопротивлений теплоотдачи и .Значения t_с1 и t_С2 определяются из уравнений (к).

Принцип расчета теплового потока через цилиндрическую стенку аналогична как и для плоской стенки. Рассмотрим однородную трубу (рис.12.2) с теплопроводностью l, внутренний диаметр d1, наружный диаметр d2, длина l. Внутри трубы находится горячая среда с температурой t'ж, а снаружи холодная среда с температурой t^''_ж

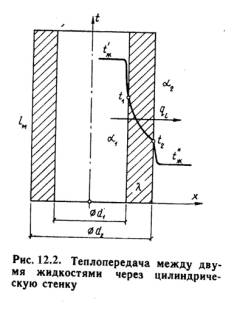
Количество теплоты, переданной от горячей среды к внутренней стенке трубы по закону Ньютона-Рихмана имеет вид: Q = p·d1·a1·l·(t'ж – t1) , (12.9) где a1 – коэффициент теплоотдачи от горячей среды с температурой t'ж к поверхности стенки• с температурой t1; Тепловой поток, переданный через стенку трубы определяется по уравнению: Q = 2·p·l·l·(t1 – t2) / ln (d2/d1). (12.10) Тепловой поток от второй поверхности стенки трубы к холодной среде определяется по формуле: Q = p·d2·a2·l·(t1 - t''ж) , (12.11) где a2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t''ж. Решая эти три уравнения получаем: Q = p l·(t'ж – t''ж) • К, (12.12) где Кl = 1/[1/(a1d1)+ 1/(2lln(d2/d1) + 1/(a2d2)] – (12.13) - линейный коэффициент теплопередачи, или Rl = 1/ Кl = [1/(a1d1)+ 1/(2lln(d2/d1) + 1/(a2d2)] – (12.14) полное линейное термическое сопротивление теплопередачи через однослойную цилиндрическую стенку. 1/(a1d1), 1/(a2d2) – термические сопротивления теплоотдачи поверхностей стенки; 1/(2lln(d2/d1) - термическое сопротивление стенки. Для многослойной (n слоев) цилиндрической стенки полное линейное термическое сопротивление будет определяться по следующей формуле: Rl = 1/ Кl = [1/(a1d1)+ 1/(2l1ln(d2/d1) + 1/(2l3ln(d3/d2) + … + 1/(2lnln(dn+1/dn) + 1/(a2dn)] – (12.15)