Критерии и задачи организации СД

Проектирование СД начинается с решения задач организации взаимодействия элементов, участвующих при диагностировании, от которых зависит качество разрабатываемой СД.

Поскольку в процессе диагностирования в общем случае участвуют три элемента (объект, средство, и ЧО), то для решения задач организации необходимо выбирать критерий, который должен зависеть от показателей элементов СД, показателей использования и диагностирования объекта. Таким критерием является функция вида (14.1).

Задачи организации СД формулируются в зависимости от задач проектирования с учетом зависимости (14.1) и имеющейся информации:

определение показателей, обеспечивающих максимум критерия организации К_max;

определение показателей, обеспечивающих требуемое значение критерия организации К_тр.

Рассмотрим самые распространенные постановки задач организации СД.

1. Определение показателей П₁, П₂, П₃, И, Д, обеспечивающих К_max или К_тр, является наиболее общей задачей.

2. Заданы организация использования И и диагностирования Д. Определить П₁, П₂, П₃, обеспечивающие К_max или К_тр.

3. Заданы требования к элементам системы диагностирования П₁, П₂, П₃. Определить требования к режимам использования И и диагностирования Д, обеспечивающие К_max или К_тр.

4. Объект диагностирования разработан (известны П₁) и для него жестко заданы режимы использования И и диагностирования Д. Определить требования к средствам диагностирования П₂ и человеку-оператору П₃, обеспечивающие К_max или К_тр.

5. Известны показатели организации использования И, диагностирования Д, элементов систем диагностирования П1, П2, П3. Определить значение критерия К.

Первые четыре задачи оптимизационные, пятая – расчетная.

В связи с тем, что техническая диагностика является средством повышения ремонтопригодности и поддержания безотказности ОД, желательно, чтобы критерий К зависел от показателей безотказности, ремонтопригодности и приспособленности к диагностированию. Для этого в дальнейшем будем считать, что показатели П₁, П₂, П₃ включают эти показатели, т.е. П₁ = (Б₁,Р_п1,П_д1); П₂ = (Б₂,Р_п2,П_д2); П₃ = (Б₃,П_д3), где Б₁,Б₂,Б₃ – показатели безотказности, Р_п1,Р_п2 – показатели ремонтопригодности; П_д1,П_д2,П_д3 – показатели приспособленности к диагностированию ОД, ТСД и ЧО. С учетом этого количество задач организации СД может значительно увеличиться.

Сформулируем математическую постановку задачи в общем виде. Если обозначить через Х={x_i} показатели, входящие в К, то постановку задачи можно представить следующим образом. Известно несколько показателей x_i, . Требуется так выбрать значения остальных показателей x_j, , чтобы К = f(x₁,...,x_i,...,x_n) = f(X) достиг значений К_max или К_тр. Математическая постановка задачи в первом случае имеет вид:

;

при ограничениях ( – нижнее и верхнее граничные значения j-го показателя).

Если показатели в пределах изменяются монотонно, то решение задачи находится в области О на границах полученных значений

.

Например, для показателей время диагностирования =0,1–0,4 ч, интенсивность отказов 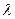= 0,001–0,01 1/ч, время восстановления = 2 – 5 ч; лучшими являются 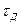= 0,1 ч, 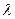= 0,001 1/ч, = 2ч.

Во втором случае для обеспечения требуемого уровня критерия организации К_тр необходимо решить уравнение:

К(Х) = К_тр

при ограничениях L₁. (14.2)

Существует по крайней мере одна комбинация значений показателей х_j, которая является решением этого уравнения.

Определим целевую функцию, позволяющую свести эту задачу к оптимизационной. Обозначим через

вектор показателей, доставляющих максимум функции К(Х), т.е.:

,

где – наилучшие значения показателей.

Нам же необходимо обеспечить условие К(Х) = К_тр. Единственность решения задачи требует перевода уравнения (14.2) в число ограничений. В качестве целевой функции целесообразно использовать функцию близости векторов Х_о и Х, т.е. решения уравнения (14.2), и обеспечить в процессе оптимизации ее минимум

при ограничениях .,K(X) = K_тр.

В связи с тем, что показатели, входящие в K(X) могут различаться по величине на несколько порядков вследствие различной физической природы (вероятность, время), то, отыскивая R(X,X_о), целесообразно нормировать показатели, введя коэффициенты масштабирования.

Такая задача является универсальной. Она не зависит от количества искомых показателей x_j и необходимости минимизации или максимизации отдельных показателей. Для решения поставленной задачи может быть использован метод штрафных функций, как наиболее универсальный.