Аналитическое прогнозирование

Методы экстраполяции, используемые для определения значения прогнозируемой переменной, называются аналитическими или методами аналитического прогнозирования.

При выборе математического аппарата для решения задачи аналитического прогнозирования необходимо предварительно определить диагностические параметры. Оценить параметры каждого элемента, входящего в объект, технически сложно из-за их большего количества, поэтому стараются выбрать минимум (в пределе – 1) диагностических параметров, обеспечивающих требуемую достоверность прогнозирования изменения состояния объекта.

Выбранные параметры должны быть чувствительными к изменениям, происходящим в элементах, входящих в объект диагностирования, т.е. любая наметившаяся тенденция изменения состояния составляющих элементов должна отражаться на поведении выбранного диагностического параметра. В частности, такими параметрами могут быть коэффициент передачи, коэффициент усиления, параметры обратной связи и т.д.

Рассмотрим постановку задачи прогнозирования. Для простоты будем считать, что работоспособность объекта определяется одним параметром 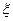. В этом случае прогнозирование работоспособности ОД рассматривается как прогнозирование изменения функции 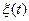, значения которой изменяются дискретно или непрерывно в интервале времени Т₁ = [t_o,t_n]. В результате этого имеются значения этой функции на интервале Т₁ (рис.9.3).

Необходимо по известным значениям 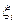определить значение функции 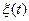: в будущие моменты времени t_n+1,...,t_n+i,...,t_n+m T₂ или узнать, через какое время значения , достигнут допустимого уровня 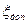. Задача может быть решена методом экстраполяционных полиномов и регрессионного анализа.

Метод экстраполяционных полиномов. Идеальным случаем решения задачи является адекватное описание изменения функции 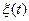каким-либо аналитическим выражением. Ввиду сложности нахождения таких выражений по дискретным точкам 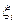целесообразно определить наилучшую структуру аналитического выражения, а при прогнозировании конкретной функции 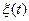– изменить базовые элементы, входящие в это выражение.

В интервале Т₁ по известным значениям 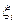необходимо найти такую функцию F(t), которая с заданной точностью описала бы процесс изменения состояния ОД, т.е. выполнить интерполяцию. В общем случае можно использовать многочлен вида

,

где a_l – неизвестные коэффициенты; – известные функции простейшего вида.

Получить многочлен F(t) значит определить коэффициенты а_l. Целесообразно использовать в качестве функций функции, имеющие наиболее простую структуру, например:

=1; =t; =t²;...; =t^r.

Тогда будем иметь базовый полином в виде:

F(t)=a_o+a₁t+a₂t²+...+a_rt^r,

графическая иллюстрация отдельных частей которого приведена на рис.9.4.

К этому виду могут быть сведены многие степенные выражения, различающиеся способом вычисления a_l.

Например, в результате измерения параметра 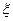в моменты времени t_o и t₁ получены его значения и (рис.9.5).

Отношение назовем средней скоростью изменения параметра в интервале [t_o,t₁]. Описать характер изменения параметра в этом интервале времени можно с помощью выражения:

F(t)=a_o+a₁t, где a_o= ; a₁= .

Если предполагать, что скорость изменения параметра сохраняется, можно прогнозировать значение параметра через время .

На практике для малых интервалов такой прогноз вполне допустим. Если известно допустимое значение 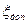диагностического параметра, то с помощью этой формулы можно определить остаточный ресурс, т.е. время, в течение которого оборудование сможет проработать до отказа:

.

Зная остаточный ресурс оборудования по каждому параметру, можно определить время его работоспособного состояния в целом, которое равно наименьшему остаточному ресурсу по всем диагностическим параметрам.

Для выполнения точного прогнозирования следует воспользоваться более сложной экстраполяционной формулой и использовать результаты не двух, а большего числа измерений.

При прогнозировании изменения состояния по одному обобщенному параметру могут быть использованы экстраполяционные полиномы Лагранжа и Ньютона.

Полином Лагранжа в общем виде можно представить следующим образом:

,

где 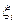– значение диагностического параметра в моменты времени t_i; L_l – коэффициенты Лагранжа.

В простейших случаях:

l=1:

l=2:

В виду того, что коэффициенты экстраполяционных полиномов не зависят от значения прогнозируемого параметра, они могут быть заранее рассчитаны и сведены в специальные таблицы, что упрощает процесс прогнозирования.

Широкое применение в прогнозировании находит полином Ньютона:

где – первая разность между измеренными величинами; – вторая разность (разность между разностями) и т.д.

Экстраполяционный полином первой степени r = 1 выглядит следующим образом:

,

а полином второй степени r = 2, соответственно,

где t берется из области Т₂ (разности t-t_n и t-t_n-1 можно выразить через число шагов прогнозирования m = 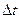соответственно m+1 и m).

Поскольку в этом случае коэффициенты при конечных разностях не зависят от прогнозируемой функции, они могут быть рассчитаны заранее и сведены в таблицы. Наличие таблиц коэффициентов экстраполяционных полиномов существенно упрощает процесс прогнозирования, т.к. сокращается объем вычислительных работ и облегчается автоматизация прогнозирования.

На практике обычно ограничиваются полиномами первой и второй степеней, поскольку скорость изменения состояния не превышает скорости реагирования полиномов. Реальные процессы протекают медленно. В этом случае кривые изменения параметров, характеризующих состояние ОД, заключены между линиями, представляющими полиномы первой (АВ) и второй (АС) степеней (рис.9.6).

При этом точность прогнозирования можно повышать, если прогнозировать только на один шаг с последующим включением полученного значения (точка А₁) в область известных значений Т₁. При этом каждое прогнозирование (на один шаг) начинается из новой точки А₁, получаемой смещением процесса на один шаг (t_o, t₁).

Количество измерений и время прогнозирования влияет на точность прогноза: чем больше n, тем точнее прогноз, т.к. удается более точно описать (интерполировать) процесс изменения параметра в области Т₁. Чем больше время, на которое осуществляется прогнозирование Т_пр, тем меньше точность, т.к. в области Т₂ могут быть учтены не все факторы. Минимальное количество требуемых измерений связано со степенью r полинома следующим образом:

n = r+1.

На практике для приемлемой точности прогноза n увеличивается в 3–5 раз.

Таким образом, использование экстраполяционных полиномов для аналитического (детерминированного) прогнозирования предполагает:

1) выбор оптимального выражения F(t) с учетом тенденции изменения параметра в области Т₁;

2) определение коэффициентов для получения точного прогноза;

3) экстраполяцию F(t) на область Т₂ и определение значения параметра в требуемый (прогнозируемый) момент времени;

4) оценивание точности прогноза.

Метод регрессионного анализа.Он основывается на использовании уравнения регрессии (лат. regressio – движение назад) вида:

,

где y – величина, характер изменения которой необходимо определить; – постоянная величина; 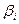– коэффициенты; x_i – параметры, влияющие на прогнозируемую величину; – взвешенная сумма; – случайная погрешность.

Это линейная зависимость y от х.

Модель изменения диагностического параметра 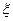во времени на основе регрессионного уравнения имеет вид:

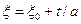, (9.1)

где – начальное значение параметра; а – коэффициент регрессии, определяющий наклон прямой.

Очевидно, что время работы ОД до отказа t_отк будет определяться допустимым значением диагностического параметра

.

Однако среди электрооборудования имеются объекты (обмотки электрических машин), для которых это значение задать невозможно. Как быть в этом случае?

Рассмотрим схему замещения обмотки электрической машины (рис.9.7). Здесь R_g – сопротивление известной величины. Основной целью прогнозирования для рассматриваемого случая является определение остаточного ресурса. В качестве диагностических параметров выступают 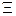= (L,R₁,C₁), где L – эквивалентная индуктивность обмотки; R₁ – эквивалентное активное сопротивление обмотки; C₁ – эквивалентная емкость обмотки.

В связи с тем, что индуктивность меняется скачком при появлении короткозамкнутых витков, этот параметр не пригоден для задачи прогнозирования. Диагностические параметры R₁ и C₁ характеризуют состояние изоляции, которая подвержена старению, и меняются монотонно. Сложность решения задачи заключается в том, что допустимые значения параметров R₁ и C₁ обмотки электрической машины неизвестны.

Исходной информацией для прогнозирования будут значения диагностических параметров R₁ и C₁, в общем случае для N машин в моменты времени t_j, где ; . По измеряемым значениям, используя метод регрессионного анализа, вычисляются значения для каждого объекта:

;

.

Для прогнозирования остаточного ресурса обмоток электрических машин необходимо определить допустимое значение диагностических параметров R_1доп и С_1доп, т.е. 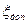. Для этого вычисляются средние значения для линейной регрессии

; .

Используя (9.1), можно осуществить прогнозирование.

В некоторых случаях (например, сопротивление изоляции обмоток электрических машин) невозможно задать допустимое значение параметра. Тогда определить его можно следующим образом.

По накопленным статическим данным определяем математическое ожидание времени отказа

,

откуда находим

.

Это значение принимается за предельно допустимое диагностического параметра.

Тогда для i-й электрической машины время отказа можно прогнозировать, воспользовавшись формулой:

Найдем время безотказной работы от момента окончания наблюдений. Разность – запас работоспособности, а – остаточный запас работоспособности. Используя формулу линейной модели изменения диагностических параметров, находим остаточный ресурс для i-й электрической машины

.

Для решения этой задачи могут быть взяты уже накопленные сведения об изменении диагностических параметров электрической машин при использовании. Такие зависимости для R₁ и C₁ для двух электрических машин приведены на рис.9.8.

Таким образом, метод предполагает:

1) выбор однотипных ОД, эксплуатирующихся в одинаковых условиях;

2) измерение значений диагностических параметров для всей совокупности ОД через определенные интервалы времени t_j;

3) вычисление средних значений по всем ОД для фиксированного момента времени t_j;

4) нахождение коэффициента регрессии а по значениям параметров в моменты времени t_j;

5) определение среднего времени безотказной работы Т_ср;

6) вычисление допустимого значения ;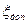

7) нахождение остаточного ресурса.

Рассмотренный метод можно использовать для оценивания состояния разнообразного электрооборудования; электрических машин, кабелей, трансформаторов, преобразователей, аккумуляторов и др.

Очевидным недостатком расчета тренда по линейной регрессии является принимаемая гипотеза о его линейности, т.к. на практике диагностические параметры могут изменяться при износе по экспоненциальному закону или иметь насыщение.