Интегральную теорему Муавра-Лапласа.

Если:

1) Число испытаний n велико

2) Оценивается вероятность Р(m₁ ,m₂ ) попадания числа успехов х в промежуток от m₁ до m_2..

3) m₁ и m₂ растут с ростом n

4) вероятность успеха постоянна

Тогда выполняется

а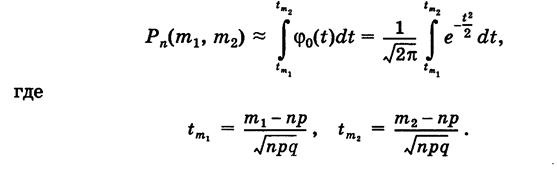

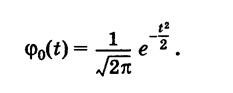(функция Гаусса)

Иначе говоря, Р(m₁ ,m₂ ) = Ф₀(t_m2 ) – Ф₀(t_m1 ), где

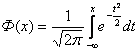- функция Лапласа.

Сделаем отступление и рассмотрим теперь функцию Лапласа отдельно.

Сформулируем свойства функции Лапласа:

1) Функция Лапласа нечетная, т.е. Φ(–t) = –Φ(t) и, соответственно, ее график симметричен относительно начала координат

2) Монотонно возрастающая

3) При х→∞ Φ→1/2, при x→ – ∞ Φ→ –1/2 , причем достаточно быстро: при х=5 Ф = 0,4(9). Поэтому при х >4 функция считается (приблизительно) равной ½

4) Существуют таблицы значений функции Лапласа, ввиду нечетности функции они составлены только для положительных значений х. Для того, чтобы воспользоваться табличными значениями функции Лапласа сначала необходимо вычислить значения аргументов

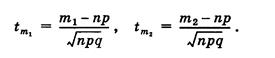
а затем найти по таблице значений функции Лапласа ее значения в этих точках.

Графиком функции Лапласа является кривая:

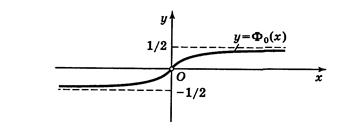
Пример 19.2.2. Игральную кость бросают 800 раз. Какова вероятность того, что число очков, кратное 3, выпадает не менее 280 и не более 294 раз?

Здесь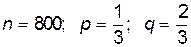

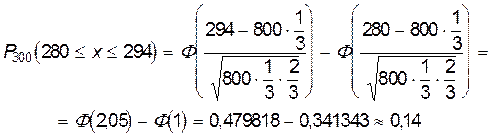
Пусть теперь в последовательности наших испытаний n достаточно велико, а p - величина очень малая и успехи редки. Тогда имеет место

Теорема Пуассона.

Асимптотическое представление P_n (x) через j(х) тем хуже, чем больше р отличается от ½ , а для случая p=0, q=1 вообще неприменимо. Однако большой круг задач связан именно с отысканием P_n (x) именно при малых значениях р.Для того, чтобы в этом случае теорема Муавра-Лапласа дала небольшую погрешность необходимо очень большое n, Поэтому требуется специальная формула, предназначенная специально для малых р, которая и приводится в теореме Пуассона:

Если

1) Число испытаний n велико

2) Мы интересуемся вероятностью P_n (x) числа успехов х в серии из n испытаний

3) р уменьшается с ростом n, т.е λ = np – константа(постоянная), т.е, рассматривается случай редких успехов.

Тогда выполняется

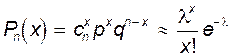
Замечание 19.2.3. Для указанной величины P_n (x) – функции Пуассона - также существуют таблицы.

Пример 19.2.3. Вероятность искажения одного символа при передаче сообщения по линии связи равна 0,001. Сообщение считают принятым, если в нем отсутствуют искажения. Найти вероятность того, что будет принято сообщение, состоящее из 20 слов по 100 символов каждое.

Предлагаемое сообщение содержит 2000 символов. Предполагая, что символы искажаются независимо, получаем схему Бернулли, в которой n=2000, p=0,001, x=0. λ = np=2. Тогда Р ₂₀₀₀(0) = 0,13534 (0! = 1)

Пример 19.2.4. Вероятность попадания в цель при каждом выстреле 0,001. Найти вероятность попадания в цель двумя и более выстрелами, если производится 5000 выстрелов.

Искомая вероятность равна 1 - Р ₅₀₀₀(0) - Р ₅₀₀₀(1) »1 – е^-5 – 5е^-5 » 0,9596