I. Графический способ отделения корней

а) Теорема. Если на отрезке [a,b] функция y=F(x) определена и непрерывна, и на его концах принимает значения разных знаков (т.е. F(a)F(b)<0), то уравнение F(x)=0 имеет на этом отрезке, по крайней мере, один корень.

Если функция y=F(x) на отрезке [a,b] строго монотонна, то корень единственный.

Требуется указать отрезок, содержащий нуль функции.

Например, пусть требуется отделить корни уравнения x²-x-1=0. Построим график функции y=x²-x-1 и укажем отрезки, содержащие точки пересечения графика функции с осью абсцисс. Искомые промежутки: [-1; 0] [1; 2].

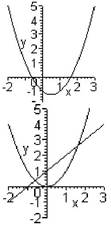
б) Иногда проще рассмотреть вместо уравнения y=F(x) равносильное ему уравнение f₁(x)=f₂(x). В этом случае требуется указать отрезок, содержащий абсциссу точки пересечения графиков функций y=f₁(x) и y=f₂(x).

Например, пусть требуется отделить корни уравнения x²-x-1=0. Рассмотрим равносильное ему уравнение x²=x+1. Тогда вместо отрезков, содержащих точки пересечения графика функции y=x²-x-1 с

осью абсцисс, можно указать отрезки, содержащие точки пересечения графиков функций f₁(x)=x² и f₂(x)=x+1.

Искомые промежутки: [-2; 0] [1; 3].

II. Отделения корней программным способом.

Пусть имеется уравнение F(x)=0, причем все корни находятся на отрезке [a,b]. Будем вычислять все значения функции y=F(x), начиная с точки x=a, двигаясь вправо шагом h. Если функция на отрезке длины h меняет знак (т.е. F(a)F(b)<0) и монотонна, можно считать, что на этом отрезке ровно 1 корень.

Правильность нахождения отрезков, содержащих один корень, зависит от характера функции y=F(x) и от величины шага h. При выборе шага должна соблюдаться «золотая середина», т.к. шаг h должен быть с одной стороны достаточно малым, чтобы не произошло потери корней, а с другой стороны не настолько маленьким, чтобы число отрезков не было слишком большим.

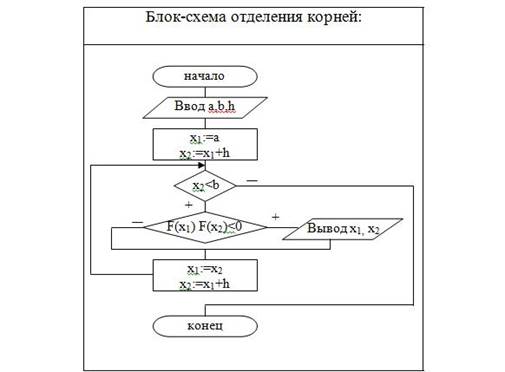
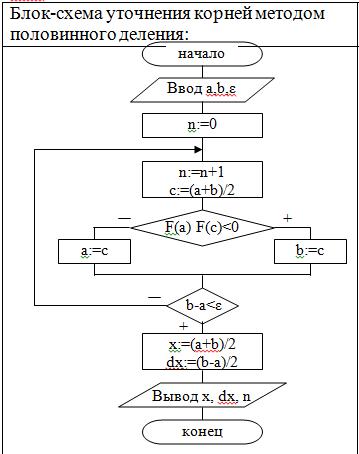
Уточнение корней методом половинного деления. Алгоритм, блок-схема.

Пусть1) функция y=F(x) определена и непрерывна на отрезке [a,b].

2) F(a)F(b)<0

Требуется найти корень на отрезке с точностью ε.

Разделим отрезок [a,b] пополам точкой c = ^{a +}₂ ^b . Если F (c) ¹ 0 , то возможны два случая:

1) F(x) меняет знак на отрезке[a; c];

2) F(x) меняет знак на отрезке[c; b].

Выбираем тот отрезок, на котором функция меняет знак. Если F(x) меняет знак на отрезке [a; c], то b:=c; если F(x) меняет знак на отрезке [c; b], то a:=c. Условие окончания счета: b - a < e .

Корень уравнения: x = ^{a +}₂ ^b . Погрешность метода: dx = ^{b -}₂ ^a .

Рассмотрим положительные и отрицательные стороны метода половинного деления.

·	«Плюсы»:	·	«Минусы»:
надежность	медленная сходимость
·	не требует приведения к	·	метод не применим для корней
специальному виду	четной кратности:

· не требует дифференцируемости

функции

· устойчив к ошибкам округления

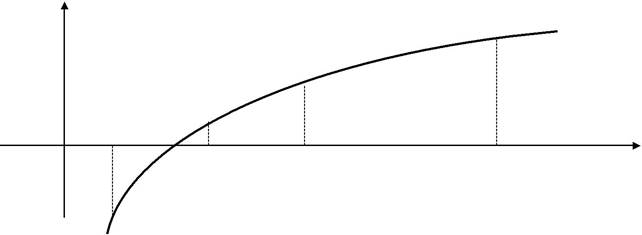
y

y=F(x)

c₂=a

O a c₁=b c₀=b b x

Число шагов при заданном ε можно оценить следующим образом: |ξ–x_k|<(b–a)/2^k+1; где x_k – это k-е приближение к корню.

ξ – точный корень.

|ξ–x_k|<(b–a)/2^k+1<ε 2^k+1>((b–a)/ε) k+1>log₂((b–a)/ε); k>log₂((b–a)/ε)–1.

Недостаток: метод трудоёмок.

Достоинство: абсолютно устойчив.