Общие сведения о временных рядах и задачах их анализа

Раздел 5. ВРЕМЕННЫЕ РЯДЫ И ПРОГНОЗИРОВАНИЕ

Лекция 3. Моделирование одномерных временных рядов и прогнозирование

План:

1. Общие сведения о временных рядах и задачах их анализа.

2. Автокорреляция уровней временного ряда.

3. Моделирование тенденции (тренда) временного ряда.

4. Моделирование периодических колебаний.

5. Прогнозирование на основе моделей временных рядов.

Сглаживание временного ряда по методу скользящей средней

Одним из методов выделения неслучайной составляющей, является метод скользящих средних. Цель сглаживания временного ряда заключается в получении ряда с меньшим разбросом уровней, что в ряде случаев позволяет на основе визуального анализа сделать вывод о наличии тенденции и ее характерных особенностях.

Метод скользящих средних основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени «скользит» вдоль ряда.

Сглаживание временного ряда по методу скользящей средней заключается в замене исходных уровней ряда y_t, сглаженными значениями y’_t, которые получаются как среднее значение определенного числа уровней исходного ряда, симметрично окружающих значение у_t. В результате получается временной ряд y’_t меньше подверженный колебаниям. Если индивидуальный разброс значений временного ряда около своего среднего значения а характеризуется дисперсией σ², то средняя из m членов ряда (у₁ + у₂ +... + у_m)/m будет иметь в m раз меньшую дисперсию (σ²/m).

Для вычисления сглаженных значений y’_t по методу простой скользящей средней используются следующие формулы:

1) Нечетный интервал сглаживания g = 2p+1 (интервал сглаживания -количество исходных уровней ряда y_t, используемых для сглаживания):

,

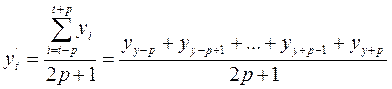где у_t- фактическое значение уровня исходного ряда в момент t, у'_t- значение скользящей средней в момент t,2p+l - длина интервала сглаживания.

2) Четный интервал сглаживания g = 2р:

.

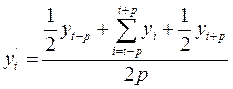Отметим, что важным свойством процедуры сглаживания является полное устранение периодических колебаний из временного ряда, если длина интервала сглаживания берется равной или кратной периоду колебаний. Это обстоятельство используется при выделении периодической составляющей временного ряда.

Моделирование периодических колебаний

Раздел 5. ВРЕМЕННЫЕ РЯДЫ И ПРОГНОЗИРОВАНИЕ

Лекция 3. Моделирование одномерных временных рядов и прогнозирование

План:

1. Общие сведения о временных рядах и задачах их анализа.

2. Автокорреляция уровней временного ряда.

3. Моделирование тенденции (тренда) временного ряда.

4. Моделирование периодических колебаний.

5. Прогнозирование на основе моделей временных рядов.

Общие сведения о временных рядах и задачах их анализа

При построении эконометрической модели используются два типа данных:

1) данные, характеризующие совокупность различных объектов в определенный момент (период) времени;

2) данные, характеризующие один объект за ряд последовательных моментов времени.

Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.

Временной ряд — это ряд наблюдаемых значений изучаемого показателя, расположенных в хронологическом порядке или в порядке возрастания времени. Наблюдения y_t (t = l..n), из которых состоит временной ряд, называются уровнями этого ряда. Отдельно взятый временной ряд можно считать выборкой из бесконечного ряда значений показателей во времени (табл. .1).

Таблица 1.

В таблице величины y_i называются уровнями ряда, а t_i – временными метками (моментами или интервалами наблюдения). Обычно рассматриваются временные ряды с равными интервалами между наблюдениями, в качестве значений t_i берутся порядковые номера наблюдений и временной ряд представляется в виде последовательности y₁, y₂ ,..., y_n , где n – количество наблюдений.

Если уровень временного ряда фиксирует значение изучаемого показателя на определенный момент времени, то такой ряд называется моментным. Если уровень временного ряда характеризует значение показателя за определенный период времени, то такой ряд является интервальным. Если уровни ряда представлены в виде производных величин (средних или относительных показателей), то такие ряды называются производными.

При изучении временных рядов выделяют две основные цели:

1) характеристику структуры ряда;

2) построение модели ряда в целях прогнозирования будущих уровней временного ряда на основании прошлых и настоящих уровней.

Для достижения этих целей необходимо идентифицировать модель временного ряда и описать ее. Идентификация модели предполагает выявление основных компонент, содержащийся в изучаемом временном ряду.

Данные, представленные в виде временных рядов, могут содержать два вида компонент — это систематическая и случайная составляющие.

Систематическая составляющая является результатом воздействия постоянно действующих факторов. Выделяют три основные систематические компоненты временного ряда: тренд, сезонность, цикличность.

Тренд (Т) представляет собой систематическую линейную или нелинейную компоненту, изменяющуюся во времени. Трендом или тенденцией развития называется сформировавшееся направление развития явления во времени под воздействием постоянно действующих факторов, например, устойчивое увеличение или уменьшение значений уровней ряда.

Сезонные и циклические колебания (S).

Сезонность — это периодические колебания уровней временного ряда внутри года.

Цикличность — это периодические колебания, выходящие за рамки 1 года. Промежуток времени между двумя соседними вершинами или впадинами в масштабах года считается длиной цикла.

Систематические составляющие могут одновременно присутствовать во временном ряду.

Случайной составляющей (Е) называется случайный шум или ошибка, воздействующая на временной ряд нерегулярно.

На рис. 1 показан график временного ряда, на котором прослеживаются все эти три составляющие.

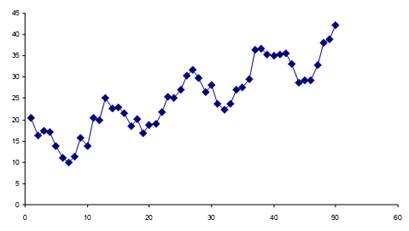
Рис. 1. Временной ряд

В зависимости от того, как объединяются во временном ряду его составляющие T, S и Е, можно получить различные модели временного ряда (Y):

– аддитивную Y_t = T_t + S_t + E_t;

– мультипликативную Y_t = T_t*S_t*E_t;

– смешанную Y_t = T_t*S_t + E_t.

При исследовании сложных экономических процессов как нам уже известно, применяются системы одновременных (структурных) уравнений. А вот для анализа развития сложных экономических процессов во времени используются системы временных рядов.

Если в таких системах временные ряды содержат сезонные или циклические колебания, то перед проведением дальнейшего исследования взаимосвязи рядов необходимо устранить сезонную или циклическую компоненту из уровней каждого ряда, поскольку ее наличие приведет к завышению истинных показателей силы и связи изучаемых временных рядов в случае, если оба ряда содержат циклические колебания одинаковой периодичности, либо к занижению этих показателей в случае, если сезонные или циклические колебания имеются только в одном из рядов или периодичность колебаний в рассматриваемых временных рядах различна.

Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции по абсолютной величине будет высоким. Для того чтобы получить коэффициенты корреляции, характеризующие причинно-следственную связь между изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде.

Влияние фактора времени сказывается также в корреляционной зависимости между значениями остатков ε_t за текущий и предыдущие моменты времени, которая получила название «автокорреляция в остатках».

Автокорреляция в остатках есть нарушение одной из основных предпосылок МНК – предпосылки о случайности остатков, полученных по уравнению регрессии. Один из возможных путей решения этой проблемы состоит в применении к оценке параметров модели обобщенного МНК.

При построении уравнения множественной регрессии по временным рядам данных, помимо двух вышеназванных проблем (влияния на корреляцию тенденции и периодических колебаний), возникает также проблема мультиколлинеарности факторов, входящих в уравнение регрессии, в случае если эти факторы содержат тенденцию.

Перед построением модели, исходные данные проверяются на сопоставимость (применение одинаковой методики получения или расчета данных), однородность (отсутствие случайных выбросов), устойчивость (наличие закономерности в изменении уровней ряда) и достаточность (число наблюдений должно в 7-10 превосходить число параметров модели).

Построение аддитивной и мультипликативной моделей сводится к расчету значений T, S и E для каждого уровня ряда.

Построение модели включает следующие шаги:

1) выравнивание исходного ряда методом скользящей средней;

2) расчет значений сезонной компоненты S;

3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной (Т + Е) или в мультипликативной (Т*Е) модели;

4) аналитическое выравнивание уровней (Т + Е) или (Т*Е) и расчет значений T с использованием полученного уравнения тренда;

5) расчет полученных по модели значений (T + S) или (T*S);

6) расчет абсолютных и/или относительных ошибок.