Неопределенный и определенный интегралы
МАТЕМАТИКА
Методические указания и индивидуальные задания
к практическим занятиям для студентов
всех направлений заочной формы обучения
Составители Н.В. Терехова
М.А. Осинцева
Тюмень
ТюмГНГУ
УДК 519.2
Математика: метод. указ. и индивид. задания для студентов, обучающихся по всем направлениям заочной формы обучения / сост. Н.В. Терехова, М.А. Осинцева; Тюменский государственный нефтегазовый университет.– 1-е изд.,.– Тюмень: Издательский центр БИК ТюмГНГУ 2012.– 32 с.
Методические указания и индивидуальные задания рассмотрены и рекомендованы к изданию методическим семинаром кафедры высшей математики
«13» марта 2012 года, протокол № 5.
Зав. кафедрой ВМ,
доцент, канд.тех. наук _________________ В.В. Проботюк
Аннотация
Методические указания и индивидуальные задания по дисциплине «Математика» предназначены для студентов, обучающихся по всем направлениям заочной формы обучения. Данная дисциплина изучается в четырех семестрах.
Введение.
Методические указания раскрывают содержание основных понятий и теорем разделов «Неопределенный и определенный интегралы» и «Дифференциальные уравнения» курса «Математика».
В каждом параграфе приводятся необходимые теоретические сведения, состоящие из определений и основных математических понятий данных разделов. В указания включены типовые задачи, для наглядности сопровождаемые иллюстрациями, и подробно рассматриваются методы их решения.
В течение семестра студент выполняет задания, номера которых заканчиваются той же цифрой, что и номер его учебного шифра. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
Разделы «Неопределенный и определенный интегралы» и «Дифференциальные уравнения», изучающиеся студентами в 3 семестре, позволяет формировать следующие общенаучные и прикладные компетенции владеть культурой мышления, способностью к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения; уметь логически верно, аргументировано и ясно строить устную и письменную речь; способен использовать законы и методы математики, естественных, гуманитарных и экономических наук при решении профессиональных задач.
Критерии оценки выполнения студентами контрольной работы
Оценка «отлично»: полное, правильное и самостоятельное выполнение работы; подробное и аккуратное оформление работы.
Оценка «хорошо»: полное и правильное выполнение работы с консультацией преподавателя; своевременная сдача работы; подробное и аккуратное оформление работы с незначительными отклонениями в оформлении.
Оценка «удовлетворительно»: выполнение работы в полном объеме с многочисленными консультациями, наличие неточностей, недочетов; несвоевременная сдача работы; небрежное оформление.
Оценка «неудовлетворительно»: выполнение работы в неполном объеме; наличие ошибок, недочетов; несвоевременная сдача контрольной работы; отклонения в оформлении.
Неопределенный и определенный интегралы.
Дифференциальные уравнения.
Неопределенный и определенный интегралы
Таблица основных интегралов
1. 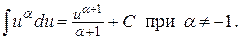 2.
2. 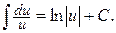
3. 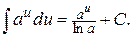 4.
4. 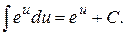
5. 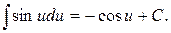 6.
6. 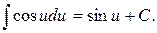
7. 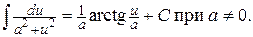 8.
8. 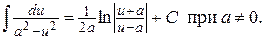
9. 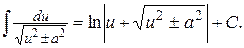 10.
10. 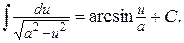
11. 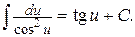 12.
12. 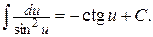
13. 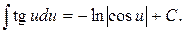 14.
14. 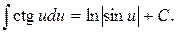
Под знак дифференциала
1. Подведение под знак дифференциала выражения вида 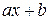
При нахождении интегралов 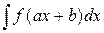 используется равенство
используется равенство 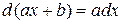 . Интеграл принимает вид:
. Интеграл принимает вид:
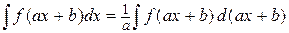 .
.
Пример1. Найти интеграл 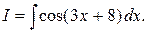
Решение. 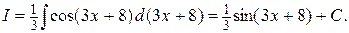
Воспользовались формулой 6, где 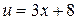 .
.
Пример2. Найти интеграл 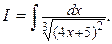 Решение.
Решение. 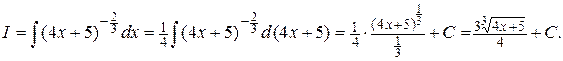
2. Подведение функции под знак дифференциала
Пример1. Найти интеграл 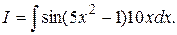
Решение. Выполняется равенство 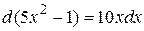 . В данном интеграле вместо
. В данном интеграле вместо 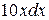 запишем
запишем 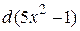 и применим формулу 5, где
и применим формулу 5, где 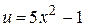 :
: 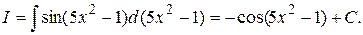
Пример2. Найти интеграл 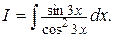
Решение. 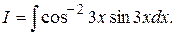 Подведем под знак дифференциала функцию
Подведем под знак дифференциала функцию 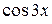 . Найдем дифференциал от этой функции:
. Найдем дифференциал от этой функции: 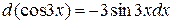 . В данном интеграле сделаем замену
. В данном интеграле сделаем замену 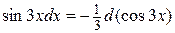 :
:
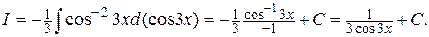
В последнем интеграле воспользовались формулой 1, где 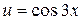 .
.
4. Интегралы 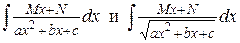
сводятся к табличным интегралам следующим приёмом.
В числителе выделяем производную квадратного трёхчлена
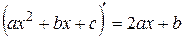 .
. 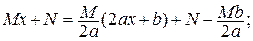
Тогда 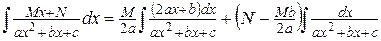 .
.
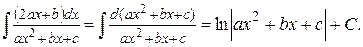
В знаменателе второго интеграла выделяют полный квадрат и используют формулы 7 или 8.
Если в знаменателе корень из квадратного трёхчлена, то аналогичные преобразования приведут к интегралам типа 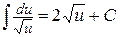 и использованию формул 9 или 10.
и использованию формул 9 или 10.
Пример 1. Найти интеграл 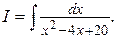
Решение. В знаменателе подынтегральной функции выделим полный квадрат и по формуле 7 получим:
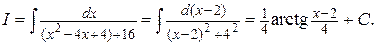
Пример 2. Найти интеграл 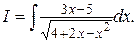
Решение. Выделим в числителе производную квадратного трёхчлена: 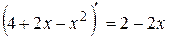 ,
, 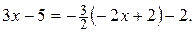 Получим:
Получим:
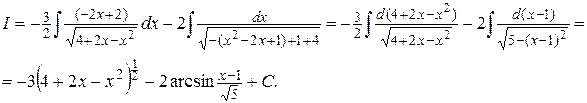
Метод подстановки
Справедливо равенство 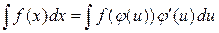 , где
, где 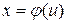 –дифференцируемая функция. После вычислений интеграла надо сделать обратную подстановку
–дифференцируемая функция. После вычислений интеграла надо сделать обратную подстановку 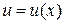 . Конечно, этим методом целесообразно пользоваться, если после подстановки интеграл упрощается.
. Конечно, этим методом целесообразно пользоваться, если после подстановки интеграл упрощается.
Пример 1. Найти интеграл 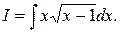
Решение.
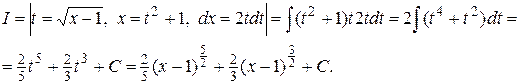
Выбор подстановки требует определенного опыта и искусства, но для некоторых классов функций можно дать рекомендации.
1.Интегрирование линейных иррациональностей
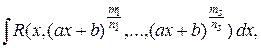 где R – рациональная функция своих аргументов. Интеграл сводится к интегрированию рациональной дроби подстановкой
где R – рациональная функция своих аргументов. Интеграл сводится к интегрированию рациональной дроби подстановкой 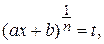 где
где 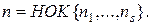
Пример 2. Найти интеграл 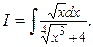
Решение. 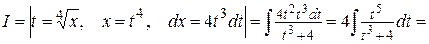
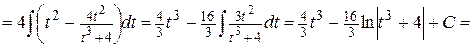
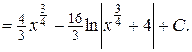
2. Интегрирование квадратичных иррациональностей. Тригонометрические подстановки
Интегралы вида 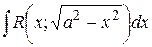 ,
, 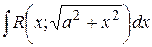 ,
, 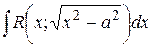 приводятся к интегралам от рациональной функции относительно
приводятся к интегралам от рациональной функции относительно 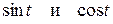 с помощью надлежащей тригонометрической подстановки: для первого интеграла
с помощью надлежащей тригонометрической подстановки: для первого интеграла 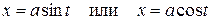 , для второго
, для второго 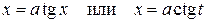 и для третьего
и для третьего 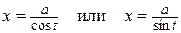 .
.
Пример 3. Найти интеграл 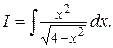
Решение. 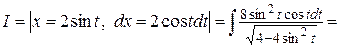
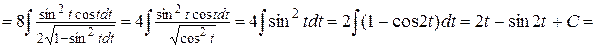
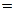
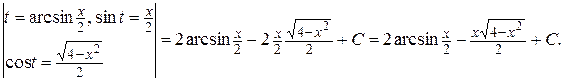
Пример 4. Найти интеграл 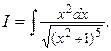
Решение. 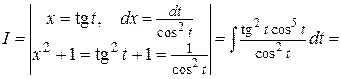
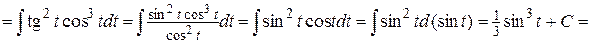
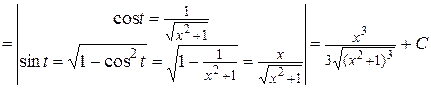 .
.
3. Универсальная тригонометрическая подстановка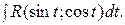
Под интегралом имеем рациональное выражение относительно 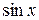 и
и 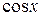 . Такие интегралы приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки
. Такие интегралы приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки 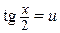 . В этом случае:
. В этом случае: 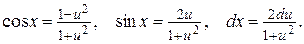
Пример 5. Найти интеграл 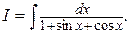
Решение. 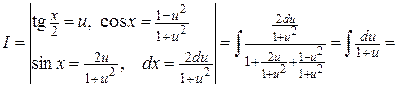
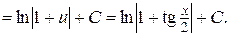
Определенный интеграл
Пусть функция 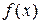 определена на отрезке
определена на отрезке 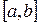 . Разделим отрезок
. Разделим отрезок 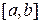 на
на 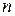 произвольных частей точками
произвольных частей точками 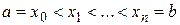 , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке 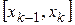 произвольную точку
произвольную точку 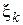 и найдем длину каждого такого отрезка:
и найдем длину каждого такого отрезка: 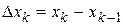 .
.
Интегральной суммой для функции 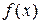 на отрезке
на отрезке 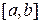 называется сумма вида
называется сумма вида 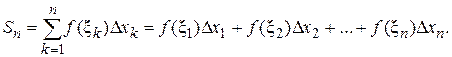
Определенным интегралом от функции 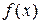 на отрезке
на отрезке 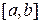 называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
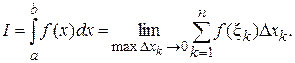
Если функция 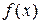 непрерывна на отрезке
непрерывна на отрезке 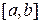 , то определенный интеграл существует.
, то определенный интеграл существует.
Числа 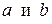 соответственно называются нижним и верхним пределами интегрирования.
соответственно называются нижним и верхним пределами интегрирования.
Методы вычислений
Формула Ньютона-Лейбница
Если 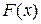 – некоторая первообразная для функции
– некоторая первообразная для функции 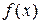 , то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница:
, то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница:
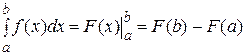 .
.
Эта формула устанавливает связь между неопределенным и определенным интегралами.
Примеры. Вычислить интегралы.
1. 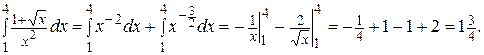
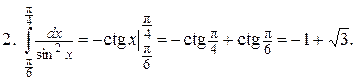
Интегрирование по частям
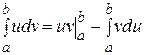
где 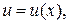
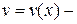 непрерывно дифференцируемые функции на отрезке
непрерывно дифференцируемые функции на отрезке 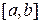 .
.
Примеры. Вычислить интегралы.
1. 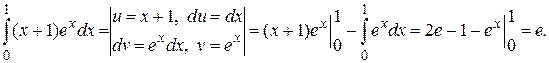
2. 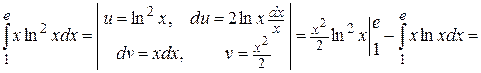
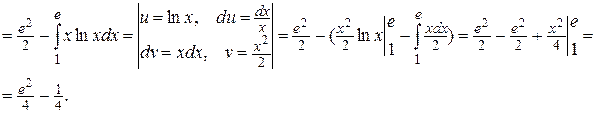
Дифференциальные уравнения
Уравнения первого порядка
Основные понятия
Уравнение 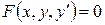 или
или 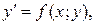 (I)
(I)
связывающее независимую переменную х, искомую функцию 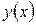 и её производную
и её производную 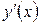 называется дифференциальным уравнением первого порядка.
называется дифференциальным уравнением первого порядка.
Решением дифференциального уравнения (I) называется такая дифференцируемая функция 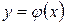 , которая при подстановке в уравнение обращает его в тождество.
, которая при подстановке в уравнение обращает его в тождество.
Общим решением дифференциального уравнения (I) называется функция, зависящая от х и одной произвольной постоянной 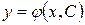 и обладающая следующими свойствами:
и обладающая следующими свойствами:
1) она является решением уравнения при любых значениях постоянной С,
2) для любого начального условия 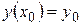 существует единственное
существует единственное 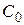 , при котором решение
, при котором решение 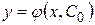 удовлетворяет заданному начальному условию.
удовлетворяет заданному начальному условию.
Всякое решение 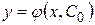 , получающееся из общего решения
, получающееся из общего решения 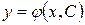 при конкретном значении
при конкретном значении 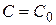 , называется частным решением дифференциального уравнения.
, называется частным решением дифференциального уравнения.
Уравнения второго порядка
1. Основные определения
Дифференциальное уравнение второго порядка имеет вид
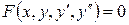 или
или 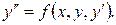
Общее решение уравнения второго порядка зависит от 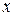 и двух произвольных постоянных
и двух произвольных постоянных 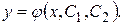
Частное решение определяется двумя начальными условиями 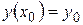 и
и 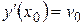 . Рассмотрим три вида уравнений, которые допускают понижение порядка.
. Рассмотрим три вида уравнений, которые допускают понижение порядка.
2. Уравнения вида 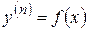
Решение такого уравнения находится интегрированием n раз.
Пример. Найти общее решение дифференциального уравнения 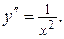 Решение.
Решение. 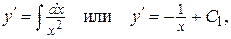
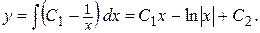
Литература
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах - ч.I, II – М.: Высшая школа, 1986.
2. Письменный Д.Т. Конспект лекций по высшей математике –
ч.I,II– М.: Рольф, 2001.
3. Шипачев В.С. Высшая математика. М.: Высшая школа, 1990.
МАТЕМАТИКА
3 семестр
Методические указания и индивидуальные задания
Составитель
ТЕРЕХОВА Наталья Владимировна
ОСИНЦЕВА Марина Александровна
Подписано в печать Формат 60х90 1/16. Усл. печ. л. 2.
Тираж 30 экз. Заказ № .
МАТЕМАТИКА
Методические указания и индивидуальные задания
к практическим занятиям для студентов
всех направлений заочной формы обучения
Составители Н.В. Терехова
М.А. Осинцева
Тюмень
ТюмГНГУ
УДК 519.2
Математика: метод. указ. и индивид. задания для студентов, обучающихся по всем направлениям заочной формы обучения / сост. Н.В. Терехова, М.А. Осинцева; Тюменский государственный нефтегазовый университет.– 1-е изд.,.– Тюмень: Издательский центр БИК ТюмГНГУ 2012.– 32 с.
Методические указания и индивидуальные задания рассмотрены и рекомендованы к изданию методическим семинаром кафедры высшей математики
«13» марта 2012 года, протокол № 5.
Зав. кафедрой ВМ,
доцент, канд.тех. наук _________________ В.В. Проботюк
Аннотация
Методические указания и индивидуальные задания по дисциплине «Математика» предназначены для студентов, обучающихся по всем направлениям заочной формы обучения. Данная дисциплина изучается в четырех семестрах.
Введение.
Методические указания раскрывают содержание основных понятий и теорем разделов «Неопределенный и определенный интегралы» и «Дифференциальные уравнения» курса «Математика».
В каждом параграфе приводятся необходимые теоретические сведения, состоящие из определений и основных математических понятий данных разделов. В указания включены типовые задачи, для наглядности сопровождаемые иллюстрациями, и подробно рассматриваются методы их решения.
В течение семестра студент выполняет задания, номера которых заканчиваются той же цифрой, что и номер его учебного шифра. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
Разделы «Неопределенный и определенный интегралы» и «Дифференциальные уравнения», изучающиеся студентами в 3 семестре, позволяет формировать следующие общенаучные и прикладные компетенции владеть культурой мышления, способностью к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения; уметь логически верно, аргументировано и ясно строить устную и письменную речь; способен использовать законы и методы математики, естественных, гуманитарных и экономических наук при решении профессиональных задач.
Критерии оценки выполнения студентами контрольной работы
Оценка «отлично»: полное, правильное и самостоятельное выполнение работы; подробное и аккуратное оформление работы.
Оценка «хорошо»: полное и правильное выполнение работы с консультацией преподавателя; своевременная сдача работы; подробное и аккуратное оформление работы с незначительными отклонениями в оформлении.
Оценка «удовлетворительно»: выполнение работы в полном объеме с многочисленными консультациями, наличие неточностей, недочетов; несвоевременная сдача работы; небрежное оформление.
Оценка «неудовлетворительно»: выполнение работы в неполном объеме; наличие ошибок, недочетов; несвоевременная сдача контрольной работы; отклонения в оформлении.
Неопределенный и определенный интегралы.
Дифференциальные уравнения.
Неопределенный и определенный интегралы
