Кинематическое исследование механизмов
ПОСТРОЕНИЕ ПЛАНА МЕХАНИЗМА.
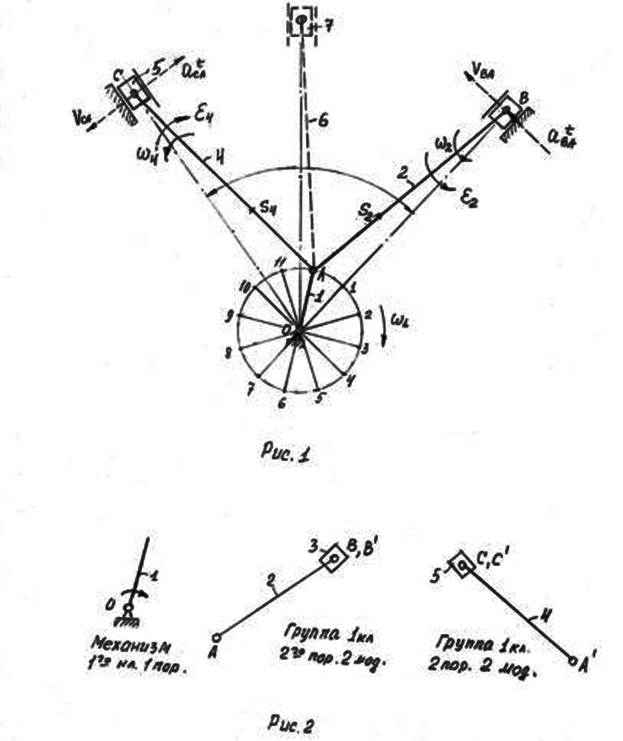
Компрессоры подвижного состава железных дорог Российской Федерации одноцилиндровые и многоцилиндровые состоят из кривошипа (коленчатого вала) и присоединенных к нему структурных групп (группы Ассура). Например, V- образный компрессор (рис.1), независимо от угла между осями цилиндров α состоит из кривошипа 1,шатунов 2 и 4, ползунов (поршней) 3 и 5. С точки зрения структуры этого механизма он состоит из механизма 1го класса 1го порядка (звено 1) двух структурных групп 1го класса 2го порядка 2 модификации (рис.2).
Присоединением к кривошипу еще одной структурной группы можно получить 3-х цилиндровый механизм (звенья 6 и 7 на рис.1).
Кинематический расчет механизма компрессора сводится к расчету параметров движения звеньев, входящих в состав указанных групп. При этом алгоритм определения этих параметров будет одним и тем же для каждой группы независимо от положения звеньев в механизме.
Для кинематического расчета механизма задается его кинематическая схема с указанием размеров звеньев, положение кривошипа в рассматриваемый момент времени и скорость его вращения.
План механизма (кинематическая схема) для выполнения расчетов графоаналитическим методом строится с использованием масштаба.
При расчете механизмов часто применяют так называемый масштабный коэффициент Кℓ, равный отношению действительных размеров звеньев к их размерам на чертеже, т.е.
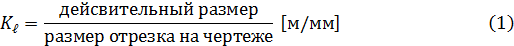
Например, действительная длина кривошипа ℓOA= 0.05м, отрезок ОА, изображающей его на чертеже, примем ОА=25мм.
Масштабный коэффициент Кℓ при этом будет равен:
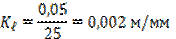
т.е. в 1мм чертежа содержится 2мм действительного размера. Фактически это масштаб уменьшения 1:2.
Иногда при построении кинематической схемы механизма необходимо определить недостающие размеры звеньев. Пусть,например, задано λ=ℓOA/ℓAB (параметр механизма), тогда длина ℓAB при заданном ℓOA и λ определится из соотношения ℓAB =ℓOA/ λ.
Разделив размеры всех звеньев на принятый масштабный коэффициент, найдем отрезки, изображающие их на чертеже.
Для выбора заданного положения кривошипа траектория точки А (окружность)разбивается на 12 равных частей от начала отсчета, в качестве которого чаще всего принимается положение точки А на линии ОВ. Отсчет положений точки А ( по часовой или против часовой стрелки) производится в зависимости от заданного направления вращения кривошипа.
Положение точек В и С на линии ОВ и ОС находим методом «засечек» циркулем, установленным в точку А и содержащим размер звеньев АВ и АС, в принятом масштабе. На звеньях АВ и ВС необходимо указать положение их центров масс (в соответствии с заданием).
Размеры прямоугольников, изображающих поршни компрессора 3 и 5 не должны соответствовать их действительным размерам и выбираются произвольно как условное изображение поступательно движущихся звеньев.
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ЗВЕНЬЕВ МЕХАНИЗМА С ПОМОЩЬЮ ПЛАНА СКОРОСТЕЙ.
Обычно принимается что кривошип вращается с постоянной угловой скоростью. Линейная скорость точки А кривошипа, как известно, определяется по формуле:
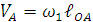
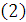
где ω1-угловая скорость вращения кривошипа, которую определим по формуле
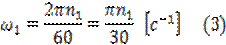
Здесь n1-число оборотов кривошипа в мин.
Вектор скорости точки, движущейся по какой-либо траектории всегда направлен по касательной к траектории в этой точке. В нашем случае вектор скорости в точке А направлен по касательной к окружности в точке А, т.е. перпендикулярен к радиусу ОА. Из произвольной точки PV на плоскости проводим отрезок 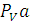 произвольной длины, который будет в масштабе
произвольной длины, который будет в масштабе 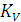 (масштабный коэффициент скорости) изображать скорость точки. Величина
(масштабный коэффициент скорости) изображать скорость точки. Величина 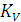 будет равна:
будет равна:
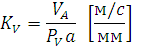
т.е. масштабный коэффициент показывает сколько единиц скорости содержится в одном миллиметре отрезка 
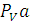 .
.
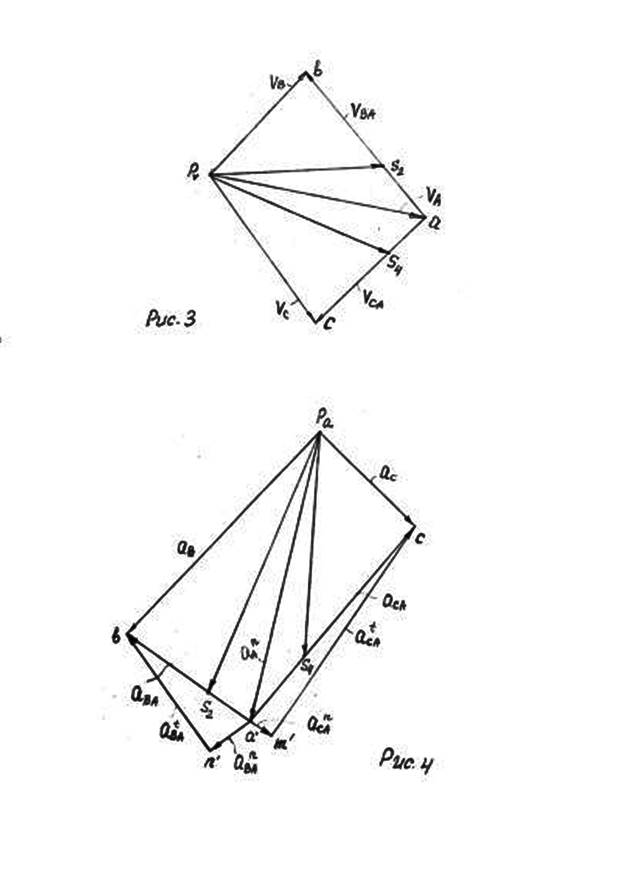
Далее определяем скорость точки В, принадлежащей одновременно звеньям 2 и 3. Звено 2 совершает сложное плоскопараллельное движение. В сложном движении скорость точки В определим в соответствии с векторным уравнением:
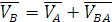 (4)
(4)
где 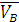 - вектор скорости точки В
- вектор скорости точки В
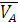 - вектор скорости точки А
- вектор скорости точки А
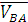 - вектор скорости точки В относительно А.
- вектор скорости точки В относительно А.
В векторном уравнении (4) скорость точки А известна по величине и по направлению, скорости VB и VA известны только по направлению. Скорость точки В направлена по линии ОВ(движение ползуна-поршня 3 по направляющим), вектор скорости точки В относительно точки А будет направлен перпендикулярно отрезку АВ как радиусу окружности, описываемой точкой В в ее относительном движении вокруг точки А. В соответствии с этим из точки PV проводим луч параллельный линии ОВ, а из точки 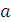 отрезка
отрезка 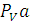 луч, перпендикулярный АВ. Пересечение этих лучей в точке
луч, перпендикулярный АВ. Пересечение этих лучей в точке 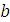 определяет отрезок
определяет отрезок 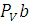 , который в принятом масштабе изображает скорость точки В, а отрезок
, который в принятом масштабе изображает скорость точки В, а отрезок 
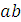 изображает скорость точки В относительно точки А.
изображает скорость точки В относительно точки А.
Направление векторов этих скоростей должно соответствовать уравнению (4), а их величина определяется из соотношений:
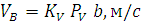
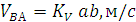
Аналогичным образом определяются скорость точки С и точки С относительно точки А.Положение точек S2 и S4( центров масс), звеньев на плане скоростей определяется в соответствии с условием подобия : их расположение не плане скоростей подобно расположению на схеме механизма. Так, например, если точка S2 находится на одной трети отрезка АВ, а точка S2 на плане скоростей будет также находиться на одной трети отрезка 
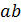 . Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скорости определится из
. Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скорости определится из
cоотношения:
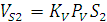 , м/c
, м/c
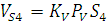 , м/c
, м/c
Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении.
Как уже говорилось, отрезок плана скоростей аb (вектор) обозначает скорость точки В относительно точки А. Разделив величину скорости 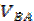 на действительную длину звена АВ получим угловую скорость звена 2, т.е.
на действительную длину звена АВ получим угловую скорость звена 2, т.е.
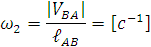
Для определения направления угловой скорости ω2 необходимо вектор скорости 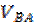 приложить к точке В (см. рис 1.). Необходимо убедиться, что звено 2 при этом будет вращаться против часовой стрелки.
приложить к точке В (см. рис 1.). Необходимо убедиться, что звено 2 при этом будет вращаться против часовой стрелки.
Угловую скорость звена 4 и ее направление определим аналогичным образом :
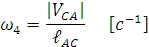
ПОСТРОЕНИЕ ПЛАНА УСКОРЕНИЙ.
Построение плана ускорений также начинаем со звена 1. В общем случае ускорение точки А, лежащей на кривошипе определится из векторного уравнения:
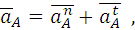
где 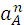 - нормальное (центростремительное) ускорение точки А.
- нормальное (центростремительное) ускорение точки А.
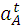 - тангенциальное ускорение точки А.
- тангенциальное ускорение точки А.
Так как кривошип вращается с постоянной угловой скоростью 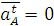
Центростремительное ускорение точки А определим по формуле:
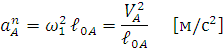
Для построения плана ускорений из произвольной точки 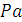 проводим луч произвольной длины( но не менее 100 мм) параллельно кривошипу. Зная величину ускорения
проводим луч произвольной длины( но не менее 100 мм) параллельно кривошипу. Зная величину ускорения  длину отрезка
длину отрезка 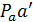 (мм) определим масштабный коэффициент ускорений
(мм) определим масштабный коэффициент ускорений 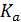 .
.
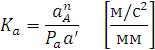
.
Ускорение точки В в сложном движении шатуна определим в соответствием с векторным уравнением :
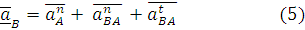
В уравнении (5) имеется 3 неизвестных по величине параметра 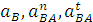
при известном их направлении. Для графического решения уравнения (5) необходимо определить величину одного из неизвестных параметров, в частности величину нормального ускорения точки В относительно точки А :
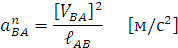
Вектор ускорения 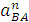 направлен от точки В к точке А параллельно шатуну АВ. Величина отрезка, изображающего ускорение
направлен от точки В к точке А параллельно шатуну АВ. Величина отрезка, изображающего ускорение 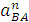 определим из
определим из
cоотношения:
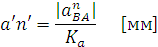
Определив величину ускорения 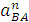 и отложив на чертеже отрезок аn' решаем уравнение (5) графически. Для этого из точки Ра (полюса плана ускорений) проводим луч, параллельный линии ОВ, который соответствует направлению вектора ускорения точки В, до пересечения с направлением вектора тангенциального ускорения
и отложив на чертеже отрезок аn' решаем уравнение (5) графически. Для этого из точки Ра (полюса плана ускорений) проводим луч, параллельный линии ОВ, который соответствует направлению вектора ускорения точки В, до пересечения с направлением вектора тангенциального ускорения 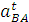 .
.
Полученная фигура является решением уравнения (5); направление векторов на этой фигуре (план ускорений) должны соответствовать уравнению (5).
Величину искомых уравнений определяем умножением соответствующих отрезков плана ускорений на масштабный коэффициент ускорений:
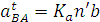
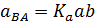
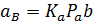
На плане ускорений, так же как на плане скоростей, определяем положение точек S2 и S4 в соответствии с теоремой подобия, после чего находим величину ускорений центров масс шатунов 2 и 4.
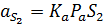
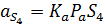
Для звеньев 4 и 5 искомые ускорения определяем аналогичным образом в соответствии с уравнениями:
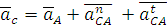
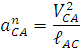
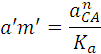
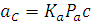
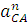
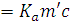
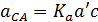
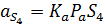
Величина и направление линейных ускорений характерных точек для звеньев 2 и 4 показана на рис. 4. План ускорений позволяет определить величину и направление угловых ускорений шатунов.
Угловое ускорение шатуна 2:
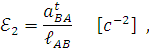
угловое ускорение шатуна 4:
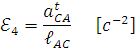
Направление этих ускорений определяется по направлению тангенциальных ускорений, приложенных в соответствующих точках (см.рис.1 и рис.4).
Планы скоростей и ускорений позволяют определить характер движения звеньев механизма. При одинаковом направлении скорости и ускорения звенья движутся ускоренно, при разном направлении- замедленно.
В нашем случае : звено-1 движется равномерно (по условию), звено 2- ускоренно, звено 3- замедленно, звено 4- замедленно, звено 5-ускоренно.
Необходимо отметить, что кинематический анализ механизма необходимо осуществлять за цикл, который в данном механизме соответствует полному обороту кривошипа.
В предположении, что кинематические параметры механизма не изменяются скачкообразно, их определяют для восьми, двенадцати и более положений кривошипа в зависимости от условий поставленной задачи.
В этом случае план механизма, планы скоростей и ускорений строятся для каждого из этих положений.
АНАЛИТИЧЕСКИМИ МЕТОДАМИ.
Кинематическое исследование механизмов методом построения планов скоростей и ускорений позволяет определить с достаточной точностью величину и характер изменения кинематических параметров механизма. Однако построение планов скоростей и ускорений для нескольких положений механизма за весь цикл значительно увеличивает объем проводимой работы, особенно для сложных механизмов. Кроме того, при этом методе значительно усложняется процесс оптимизации кинематических параметров. Из-за необходимости многократных построений планов скоростей и ускорений. При использовании вычислительной техники для кинематического исследование механизмов необходимо иметь аналитические зависимости искомых параметров, позволяющие определять их за весь цикл в соответствии с изменениям обобщенных координат.
Одним из методов аналитического исследования кинематики механизмов является метод замкнутых векторных контуров, предложенный В.А. Зиновьевым [ ].

(рис.12)
При кинематическом исследовании механизмов этим методом каждое звено механизма представляется в виде вектора определенного направления. Рассмотрим этот метод на примере кривошипно-ползунного механизма (рис.12), в котором кривошип ОА является вектором 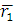 , а шатун АВ вектором
, а шатун АВ вектором 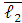 . Положение точки B в системе координат xoy обозначено вектором
. Положение точки B в системе координат xoy обозначено вектором 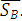 Условие замкнутости векторов при принятом направлении векторов
Условие замкнутости векторов при принятом направлении векторов 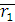 и
и 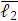 :
:
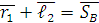 (1)
(1)
Углы 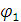 и
и 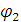 соответственно определяют положение векторов
соответственно определяют положение векторов 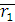 и
и 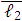 в выбранной системе координат. Спроектируем эти векторы на оси координат:
в выбранной системе координат. Спроектируем эти векторы на оси координат:
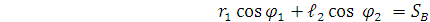 (2)
(2)
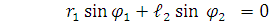 (3)
(3)
Одной из основных задач в данном случае является нахождение функции изменения кинематических параметров механизма при изменении обобщенной координаты 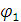 .
.
Как следует из уравнения (3):
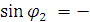
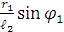 (4)
(4)
Обозначим 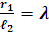 - параметр механизма, который в кривошипно-ползунных механизмов транспортных машин изменяется в пределах
- параметр механизма, который в кривошипно-ползунных механизмов транспортных машин изменяется в пределах 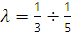
и определяет их габариты. С учетом 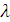 формула (4) примет вид:
формула (4) примет вид:
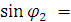
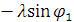 (5)
(5)
Продифференцируем уравнение (3) по времени при условии 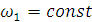 .
.
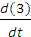
 (6)
(6)
Из уравнения (6) определим угловую скорость шатуна:
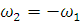
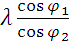 (7)
(7)
Для определения углового ускорения шатуна 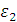 продифференцируем уравнение (6):
продифференцируем уравнение (6):
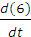
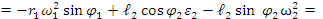 0
0
Откуда следует
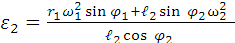 (8)
(8)
Направление угловых скоростей и ускорений определяется по соответствии их знака принятому положительному направлению отсчета углов 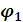 и
и 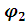 .
.
В соответствии с (5) формулу (2) представим в виде:
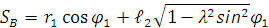
Чтобы избавиться от радикала разложим его в бесконечный ряд Маклорена:
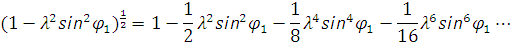
Этот ряд быстро сходится и для практических расчетов при 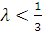 достаточно использовать два первых члена. Величина третьего члена
достаточно использовать два первых члена. Величина третьего члена 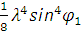 при
при 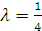 и
и 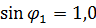 составляет
составляет 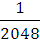 или 0,05% от единицы.
или 0,05% от единицы.
Таким образом, положение точки B можно приближенно, но с достаточной степенью точности определить по формуле:
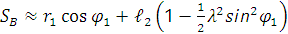 (9)
(9)
Продифференцировав дважды уравнение (9) получим также приближенные формулы для определения скорости точки B.
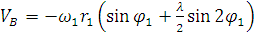 (10)
(10)
и соответственно ускорение:
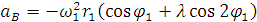 (11)
(11)
Точное значения ускорения 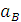 представляется в виде бесконечного тригонометрического ряда:
представляется в виде бесконечного тригонометрического ряда:
а
коэффициенты, 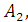
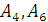 которого определяются в зависимости от величины
которого определяются в зависимости от величины 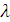 . В частности, при
. В частности, при 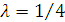 коэффициент
коэффициент 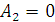 ,254, т.е. незначительно отличается от
,254, т.е. незначительно отличается от 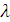 . Для других значений параметра
. Для других значений параметра 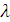 коэффициенты
коэффициенты 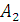 также незначительно отличаются от его величины, что потверждает возможность использования формул (10) и (11) при различных
также незначительно отличаются от его величины, что потверждает возможность использования формул (10) и (11) при различных 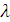 .
.
Определим экстремальные значения ускорения точки B. Для этого продифференцируем уравнение (11) по независимому переменному 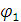 и приравняем его к нулю.
и приравняем его к нулю.
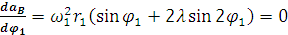 (12)
(12)
Уравнение (12) дает возможность определить угол 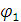 , при котором
, при котором 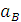 имее
имее 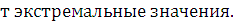
Учитывая, что 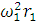 не равно нулю, и заменив
не равно нулю, и заменив 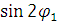 его значениями после преобразования получим:
его значениями после преобразования получим:
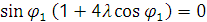
откуда 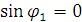 (13)
(13)
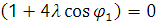 (14)
(14)
Из уравнения (13) получим значения угла 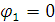 и
и 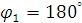 .
.
При этих значениях угла 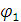 имеют место два вида уравнений, определяющих экстремальные значения ускорения
имеют место два вида уравнений, определяющих экстремальные значения ускорения 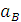 :
:
при 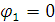 ;
; 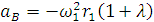
Уравнение (14) добавляет еще два дополнительных экстремальных значения в соответствии с формулой:
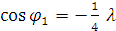
Так как 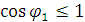 , то это уравнение справедливо, если
, то это уравнение справедливо, если 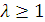 . При этом значении
. При этом значении 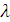 получается два угла
получается два угла 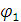 (во второй третьей четвертях), при которых ускорение
(во второй третьей четвертях), при которых ускорение 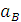 имеет экстремальные значения.
имеет экстремальные значения. 
Характер изменения ускорения 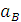 в зависимости от угла
в зависимости от угла 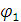 для разных значений параметра
для разных значений параметра 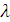 показан на (рис.13).
показан на (рис.13).
При кинематическом исследовании сложного механизма (см.рис.1), состоящего в общем из двух кривошипно-ползунных механизмов с одним кривошипом, необходимо составить расчетную схему, которая будет зависеть от расположения выбранной системы координат.
ПОСТРОЕНИЕ ПЛАНА МЕХАНИЗМА.
Компрессоры подвижного состава железных дорог Российской Федерации одноцилиндровые и многоцилиндровые состоят из кривошипа (коленчатого вала) и присоединенных к нему структурных групп (группы Ассура). Например, V- образный компрессор (рис.1), независимо от угла между осями цилиндров α состоит из кривошипа 1,шатунов 2 и 4, ползунов (поршней) 3 и 5. С точки зрения структуры этого механизма он состоит из механизма 1го класса 1го порядка (звено 1) двух структурных групп 1го класса 2го порядка 2 модификации (рис.2).
Присоединением к кривошипу еще одной структурной группы можно получить 3-х цилиндровый механизм (звенья 6 и 7 на рис.1).
Кинематический расчет механизма компрессора сводится к расчету параметров движения звеньев, входящих в состав указанных групп. При этом алгоритм определения этих параметров будет одним и тем же для каждой группы независимо от положения звеньев в механизме.
Для кинематического расчета механизма задается его кинематическая схема с указанием размеров звеньев, положение кривошипа в рассматриваемый момент времени и скорость его вращения.
План механизма (кинематическая схема) для выполнения расчетов графоаналитическим методом строится с использованием масштаба.
При расчете механизмов часто применяют так называемый масштабный коэффициент Кℓ, равный отношению действительных размеров звеньев к их размерам на чертеже, т.е.
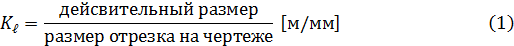
Например, действительная длина кривошипа ℓOA= 0.05м, отрезок ОА, изображающей его на чертеже, примем ОА=25мм.
Масштабный коэффициент Кℓ при этом будет равен:
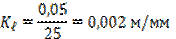
т.е. в 1мм чертежа содержится 2мм действительного размера. Фактически это масштаб уменьшения 1:2.
Иногда при построении кинематической схемы механизма необходимо определить недостающие размеры звеньев. Пусть,например, задано λ=ℓOA/ℓAB (параметр механизма), тогда длина ℓAB при заданном ℓOA и λ определится из соотношения ℓAB =ℓOA/ λ.
Разделив размеры всех звеньев на принятый масштабный коэффициент, найдем отрезки, изображающие их на чертеже.

Для выбора заданного положения кривошипа траектория точки А (окружность)разбивается на 12 равных частей от начала отсчета, в качестве которого чаще всего принимается положение точки А на линии ОВ. Отсчет положений точки А ( по часовой или против часовой стрелки) производится в зависимости от заданного направления вращения кривошипа.
Положение точек В и С на линии ОВ и ОС находим методом «засечек» циркулем, установленным в точку А и содержащим размер звеньев АВ и АС, в принятом масштабе. На звеньях АВ и ВС необходимо указать положение их центров масс (в соответствии с заданием).
Размеры прямоугольников, изображающих поршни компрессора 3 и 5 не должны соответствовать их действительным размерам и выбираются произвольно как условное изображение поступательно движущихся звеньев.
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ЗВЕНЬЕВ МЕХАНИЗМА С ПОМОЩЬЮ ПЛАНА СКОРОСТЕЙ.
Обычно принимается что кривошип вращается с постоянной угловой скоростью. Линейная скорость точки А кривошипа, как известно, определяется по формуле:
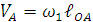
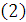
где ω1-угловая скорость вращения кривошипа, которую определим по формуле
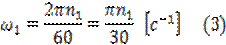
Здесь n1-число оборотов кривошипа в мин.
Вектор скорости точки, движущейся по какой-либо траектории всегда направлен по касательной к траектории в этой точке. В нашем случае вектор скорости в точке А направлен по касательной к окружности в точке А, т.е. перпендикулярен к радиусу ОА. Из произвольной точки PV на плоскости проводим отрезок 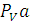 произвольной длины, который будет в масштабе
произвольной длины, который будет в масштабе 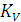 (масштабный коэффициент скорости) изображать скорость точки. Величина
(масштабный коэффициент скорости) изображать скорость точки. Величина 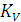 будет равна:
будет равна:
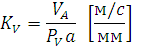
т.е. масштабный коэффициент показывает сколько единиц скорости содержится в одном миллиметре отрезка 
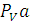 .
.
Далее определяем скорость точки В, принадлежащей одновременно звеньям 2 и 3. Звено 2 совершает сложное плоскопараллельное движение. В сложном движении скорость точки В определим в соответствии с векторным уравнением:
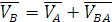 (4)
(4)
где 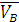 - вектор скорости точки В
- вектор скорости точки В
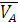 - вектор скорости точки А
- вектор скорости точки А
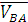 - вектор скорости точки В относительно А.
- вектор скорости точки В относительно А.
В векторном уравнении (4) скорость точки А известна по величине и по направлению, скорости VB и VA известны только по направлению. Скорость точки В направлена по линии ОВ(движение ползуна-поршня 3 по направляющим), вектор скорости точки В относительно точки А будет направлен перпендикулярно отрезку АВ как радиусу окружности, описываемой точкой В в ее относительном движении вокруг точки А. В соответствии с этим из точки PV проводим луч параллельный линии ОВ, а из точки 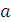 отрезка
отрезка 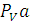 луч, перпендикулярный АВ. Пересечение этих лучей в точке
луч, перпендикулярный АВ. Пересечение этих лучей в точке 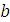 определяет отрезок
определяет отрезок 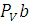 , который в принятом масштабе изображает скорость точки В, а отрезок
, который в принятом масштабе изображает скорость точки В, а отрезок 
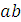 изображает скорость точки В относительно точки А.
изображает скорость точки В относительно точки А.
Направление векторов этих скоростей должно соответствовать уравнению (4), а их величина определяется из соотношений:
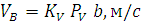
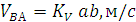
Аналогичным образом определяются скорость точки С и точки С относительно точки А.Положение точек S2 и S4( центров масс), звеньев на плане скоростей определяется в соответствии с условием подобия : их расположение не плане скоростей подобно расположению на схеме механизма. Так, например, если точка S2 находится на одной трети отрезка АВ, а точка S2 на плане скоростей будет также находиться на одной трети отрезка 
 . Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скорости определится из
. Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скорости определится из
cоотношения:
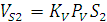 , м/c
, м/c
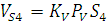 , м/c
, м/c
Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении.
Как уже говорилось, отрезок плана скоростей аb (вектор) обозначает скорость точки В относительно точки А. Разделив величину скорости 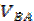 на действительную длину звена АВ получим угловую скорость звена 2, т.е.
на действительную длину звена АВ получим угловую скорость звена 2, т.е.
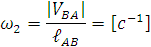
Для определения направления угловой скорости ω2 необходимо вектор скорости 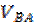 приложить к точке В (см. рис 1.). Необходимо убедиться, что звено 2 при этом будет вращаться против часовой стрелки.
приложить к точке В (см. рис 1.). Необходимо убедиться, что звено 2 при этом будет вращаться против часовой стрелки.
Угловую скорость звена 4 и ее направление определим аналогичным образом :
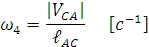
ПОСТРОЕНИЕ ПЛАНА УСКОРЕНИЙ.
Построение плана ускорений также начинаем со звена 1. В общем случае ускорение точки А, лежащей на кривошипе определится из векторного уравнения:
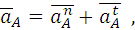
где 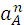 - нормальное (центростремительное) ускорение точки А.
- нормальное (центростремительное) ускорение точки А.
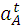 - тангенциальное ускорение точки А.
- тангенциальное ускорение точки А.
Так как кривошип вращается с постоянной угловой скоростью 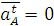
Центростремительное ускорение точки А определим по формуле:
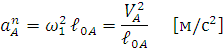
Для построения плана ускорений из произвольной точки  проводим луч произвольной длины( но не менее 100 мм) параллельно кривошипу. Зная величину ускорения
проводим луч произвольной длины( но не менее 100 мм) параллельно кривошипу. Зная величину ускорения 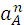 длину отрезка
длину отрезка 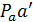 (мм) определим масштабный коэффициент ускорений
(мм) определим масштабный коэффициент ускорений 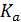 .
.
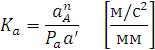
.
Ускорение точки В в сложном движении шатуна определим в соответствием с векторным уравнением :
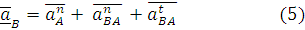
В уравнении (5) имеется 3 неизвестных по величине параметра 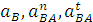
при известном их направлении. Для графического решения уравнения (5) необходимо определить величину одного из неизвестных параметров, в частности величину нормального ускорения точки В относительно точки А :
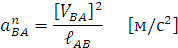
Вектор ускорения 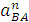 направлен от точки В к точке А параллельно шатуну АВ. Величина отрезка, изображающего ускорение
направлен от точки В к точке А параллельно шатуну АВ. Величина отрезка, изображающего ускорение 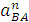 определим из
определим из
cоотношения:
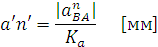
Определив величину ускорения 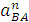 и отложив на чертеже отрезок аn' решаем уравнение (5) графически. Для этого из точки Ра (полюса плана ускорений) проводим луч, параллельный линии ОВ, который соответствует направлению вектора ускорения точки В, до пересечения с направлением вектора тангенциального ускорения
и отложив на чертеже отрезок аn' решаем уравнение (5) графически. Для этого из точки Ра (полюса плана ускорений) проводим луч, параллельный линии ОВ, который соответствует направлению вектора ускорения точки В, до пересечения с направлением вектора тангенциального ускорения 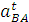 .
.
Полученная фигура является решением уравнения (5); направление векторов на этой фигуре (план ускорений) должны соответствовать уравнению (5).
Величину искомых уравнений определяем умножением соответствующих отрезков плана ускорений на масштабный коэффициент ускорений:
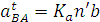
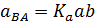
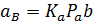
На плане ускорений, так же как на плане скоростей, определяем положение точек S2 и S4 в соответствии с теоремой подобия, после чего находим величину ускорений центров масс шатунов 2 и 4.
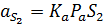
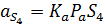
Для звеньев 4 и 5 искомые ускорения определяем аналогичным образом в соответствии с уравнениями:
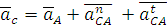
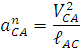
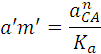
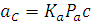
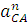
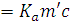
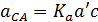
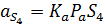
Величина и направление линейных ускорений характерных точек для звеньев 2 и 4 показана на рис. 4. План ускорений позволяет определить величину и направление угловых ускорений шатунов.
Угловое ускорение шатуна 2:
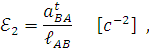
угловое ускорение шатуна 4:
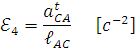
Направление этих ускорений определяется по направлению тангенциальных ускорений, приложенных в соответствующих точках (см.рис.1 и рис.4).
Планы скоростей и ускорений позволяют определить характер движения звеньев механизма. При одинаковом направлении скорости и ускорения звенья движутся ускоренно, при разном направлении- замедленно.
В нашем случае : звено-1 движется равномерно (по условию), звено 2- ускоренно, звено 3- замедленно, звено 4- замедленно, звено 5-ускоренно.
Необходимо отметить, что кинематический анализ механизма необходимо осуществлять за цикл, который в данном механизме соответствует полному обороту кривошипа.
В предположении, что кинематические параметры механизма не изменяются скачкообразно, их определяют для восьми, двенадцати и более положений кривошипа в зависимости от условий поставленной задачи.
В этом случае план механизма, планы скоростей и ускорений строятся для каждого из этих положений.

КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМОВ
АНАЛИТИЧЕСКИМИ МЕТОДАМИ.
Кинематическое исследование механизмов методом построения планов
