Классификация задач нелинейного программирования

Нелинейное программирование включает в себя методы определения минимума функции n переменных F(х), где х = || x₁, x₂, x₃ || при m + n ограничивающих условиях

g_i≤0, i=1,2,...,m; (3.1.2)

x_j≥0, j=1,2...,n; (3.1.3)

т. е.

f(x)=min(max) (3.1.4)

g≤0, x≥0. (3.1.5)

Соотношения (3.1.2, 3.1.3) следует понимать таким образом, что каждая компонента векторов имеет значение g и x не менее нуля и сокращенно их записывают в виде:

min {f(x)|x_j≥0, j=1,...,n; g_i≤0, i=1,2,...,m} (3.1.6)

или

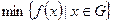, (3.1.7)

где область G задается условиями

G = {x|x≥0, g_i(x)≤0 для всех i}.

В нелинейном программировании допускаются в общем случае любые соотношения между n и m, т. е. n>m, n = m, m<m.

В задачах нелинейного программирования, так же как и в задачах линейного программирования, могут встречаться и другие формы написания условий.

В общем случае функции f(х) и g_i(х) бывают произвольными и, в частности, линейными.

Задачи поиска экстремума функции при наличии ограничений можно решать с помощью классических методов, но они рассматривают только случаи, когда неравенства имеют вид строгих равенств:

f (х) = min (max);

g_i(х) = 0.

При этом не требуется неотрицательности переменных x_j, m<n, а функции f(х) и g_i(х) непрерывны и имеют частные производные, по крайней мере до второго порядка. Для нелинейного программирования классические методы имеют большое теоретическое значение, так как основополагающая теорема Куна-Таккера в выпуклом программировании обобщает теорему Лагранжа для классических задач.

Основной недостаток методов нелинейного программирования заключается в том, что с их помощью не удается найти глобальный экстремум при наличии нескольких локальных экстремумов. Определить глобальный экстремум можно лишь методом динамического программирования. Однако его применение зависит от определенных условий, обеспечивающих выполнение принципа оптимальности Беллмана. Решение задач нелинейного программирования методом динамического программирования имеет свою специфику, благодаря которой динамическое программирование часто рассматривают в разделе нелинейного программирования. Применение дискретного принципа максимума Понтрягина для решения задач нелинейного программирования в настоящее время не разработано так детально, как применение динамического программирования. Следует заметить, что этот метод более «чувствителен» к введению ограничений на переменные.

К прямым методам поиска относят методы, в которых для отыскания экстремума не используются производные первого и высших порядков. В этих методах направления поиска определяются на основе последовательных вычислений значений функции f(x).

Теоретически нелинейное программирование разработано только для одного частного случая выпуклых функций f(х) и g_i(х), и соответственно этот раздел назван выпуклым программированием (рисунок 3.1.1).

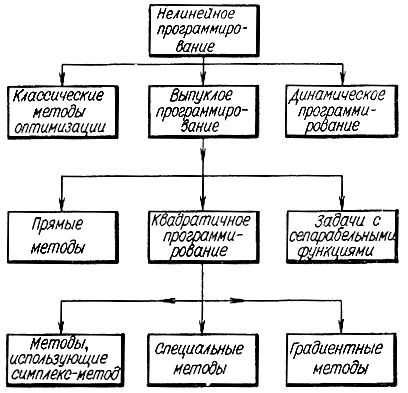
Рисунок 3.1.1 – Классификация методов нелинейного программирования

Метод считается теоретически разработанным, если найдены соотношения, являющиеся необходимыми и достаточными условиями оптимума, и алгоритмы поиска экстремума с доказательством их сходимости. Этим требованиям, строго говоря, удовлетворяют только методы, рассматриваемые в разделе квадратичного программирования, частично методы решения задач с сепарабельными функциями и в значительно меньшей степени прямые методы.

Функция f(х) = f(x₁, ...,x_n) называется сепарабельной, если она представлена в виде

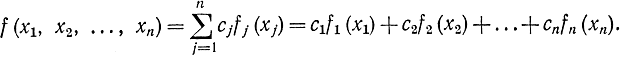
В общем случае эти функции не являются выпуклыми. Однако если каждая из функций f_j(x_j) выпуклая и коэффициенты c_j неотрицательны, то функция f(х) тоже выпуклая. Методы решения задач с сепарабельными функциями, основанные на замене нелинейных функций ломаными кривыми, составленными из отрезков прямых, ищут локальный экстремум и не гарантируют отыскание глобального экстремума.

Теоретически наиболее широко и детально в нелинейном программировании разработан раздел выпуклого программирования, называемый Квадратичным, в котором функции представляются в виде суммы линейной и квадратичной форм и имеют вид:

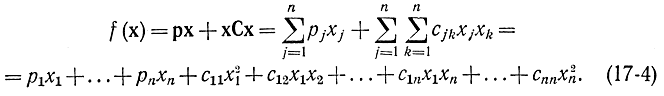
Для выпуклости необходимо, чтобы матрица C = [| c_jk || представляла собой симметричную положительную полуопределенную матрицу, т. е. чтобы для любых x выполнялись условия симметрии c_jk =c_kj и положительной полуопределенности хСх≥0.

Однако и этот достаточно узкий раздел не представляет единого целого, а состоит из набора методов, справедливых для более частных видов функции и отличающихся разной эффективностью, для которой пока еще нет удобных способов сравнительной оценки.

Методы квадратичного программирования можно разделить на три группы: алгоритмы, использующие симплекс-метод; градиентные и прочие специальные методы.

Отличие градиентных методов, рассматриваемых в квадратичном программировании, от рассмотренных в разделе прямых методов заключается в том, что в первом случае благодаря заданию функций в виде (17-4) удается получить значительно больше результатов, характеризующих конкретный метод. В прямых методах поиска в градиентных и других алгоритмах, как правило, функция цели неизвестна (считается просто, что она выпукла), в традиционных руководствах по нелинейному программированию в большинстве случаев она задана аналитически, в виде таблиц или другим способом. Прямые методы по традиции много внимания уделяют аспектам поиска «вслепую» в условиях неопределенности, выбору оптимальной в каждом случае стратегии поиска.

Задачи нелинейного программирования по сравнению с задачами линейного программирования обладают большим многообразием. На рис. 17-3 представлены возможные варианты расположения точки экстремума для случая двух переменных. Так, в случае линейных ограничений и нелинейной функции цели экстремума можно достигнуть в крайней точке (вершине) допустимой области значений (рис. 17-3, а), в одной из точек, лежащих на ограничивающих прямых (рис. 17-3, б), и, наконец, в точке, расположенной внутри области (рис. 17-3, в). Пунктирные концентрические окружности изображают линии постоянных значений функции цели, сплошные линии - границу области допустимых значений. В случае на рис. 17-3, б - экстремум определяется как точка касания прямой, ограничивающей допустимую область значений, и линии равных значений функции цели.

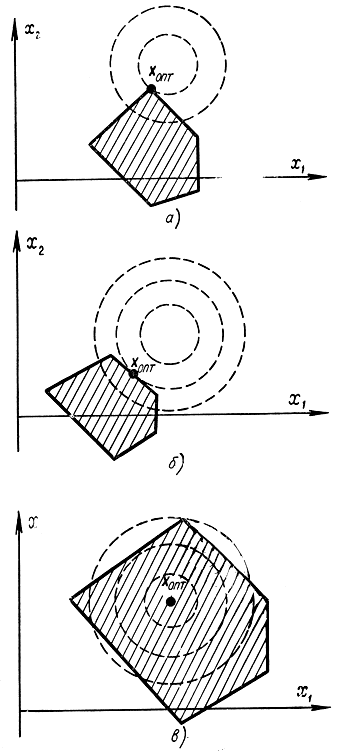
Рис. 17-3. Различные случаи оптимума в задачах нелинейного программирования

Рис. 17-4. Случай двух экстремумов при односвязной области допустимых значений

Решение задач нелинейного программирования может давать два или более экстремума, тогда как решение задач линейного программирования дает один экстремум. На рис. 17-4 показан случай, соответствующий линейным ограничениям и нелинейной (квадратичной) функции цели, где она достигает максимального значения в двух точках А (локальный максимум) и В (глобальный максимум). На этом рисунке пунктиром обозначены постоянные значения функции цели F = const = С_i, сплошной линией ограничена область допустимых значений. При нелинейных ограничениях может иметь место случай многосвязной области допустимых значений, и в каждой изолированной подобласти функция цели может достигать своего одного или нескольких локальных экстремумов. На рис. 17-5 представлен случай двусвязной области, в которой функция цели достигает локальных экстремумов. Максимум в точке В - глобальный для всей области допустимых значение, в точке А – локальный.

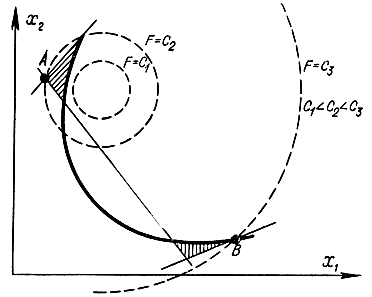
Рис. 17-5. Случай двух экстремумов при двусвязной области допустимых значений

Метод Лагранжа

Начнём рассмотрение задачи поиска экстремума функции 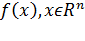с ограничениями равенствами 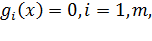с «метода множителей Лагранжа».

Алгоритм метода состоит из следующих шагов:

- составим функцию Лагранжа в виде линейной комбинации целевой функции 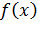и функций 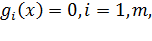взятых с коэффициентами, называемыми множителями Лагранжа – 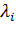: 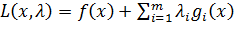; (3.2)

- будем считать все функции непрерывно дифференцируемыми и приравняем 0 градиент функции Лагранжа : ;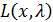

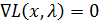- составим систему n+m уравнений, состоящих из равенства 0 градиента и уравнений ограничений:

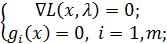(3.3)

1. найдём решения этой системы уравнений, которые будут стационарными точками задачи – определяющими необходимые условия решения задачи поиска условного экстремума.

Рассмотрим эвристические геометрические рассуждения на плоскости, помогающие понять смысл метода. Для этого рассмотрим изображённый на рисунке двумерный случай:

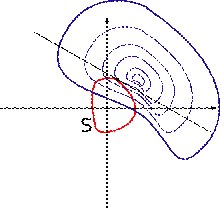
Рисунок 5.1 – Линии уровня целевой функции двух переменных f(x,y) и кривой ограничений g(x,y)

В двумерном случае имеем целевую функцию двух переменных 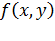при условии, задаваемом уравнением g 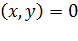. На рисунке изображены линии уровня функции 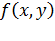(т.е. геометрическое место точек, где 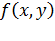=const) и кривую ограничений 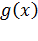. Так как все функции непрерывно дифференцируемы, то и все кривые являются гладкими. Тогда задача сводится к нахождению экстремума функции f на кривой S. Будем также считать, что S не проходит через точки, в которых градиент целевой функции равен нулю: .

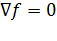В точках, где кривая S трансверсальна (пересекает под ненулевым углом) линиям уровня, двигаясь по кривой S из этой точки можно попасть как на линии уровня, соответствующие большему значению, так и меньшему значения функции f. Следовательно, такая точка не может быть точкой экстремума, и стационарными точками являются такие точки, где кривые пересекаются под нулевым углом, т.е. их касательные параллельны и градиенты пропорциональны:

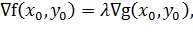(3.4)

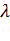- некоторое число, отличное от нуля, являющееся множителем Лагранжа.

В общем многомерном случае условию аналогичному параллельности касательных является параллельность касательных плоскостей, которому также соответствует пропорциональность градиентов.

Рассмотрим регулярный случай, т.е. невырожденность градиента, и рассмотрим функцию Лагранжа, как зависящую также и от :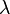

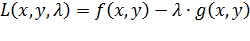. (3.5)

Необходимым условием ее экстремума является равенство нулю градиента функции трёх переменных x, y, :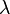

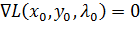. (3.6)

В соответствии с правилами дифференцирования, оно записывается в виде равенства 0 частных производных по x, y и уравнения ограничения.

Мы получили систему, первые два уравнения которой эквивалентны необходимому условию локального экстремума (1), а третье — уравнению g 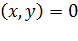. Из нее можно найти 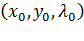. При этом 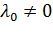, поскольку в противном случае градиент функции f обращается в нуль в точке 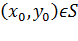, что противоречит нашим предположениям. Следует заметить, что найденные таким образом точки 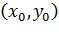могут и не являться искомыми точками условного экстремума, ведь рассмотренное условие носит необходимый, но не достаточный характер. Нахождение условного экстремума с помощью вспомогательной функции 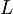и составляет основу метода множителей Лагранжа, примененного здесь для простейшего случая двух переменных. Оказывается, вышеприведенные рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.

На основе метода множителей Лагранжа можно доказать и некоторые достаточные условия для условного экстремума, требующие анализа вторых производных функции Лагранжа.