Способы решения задач нелинейного программирования.

3.2.1..Графоаналитический метод.

Рассмотрим задачу нелинейного программирования следующего содержания.

Предприятие выпускает изделия двух видов, используя два вида сырья, запасы которого 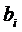в рассматриваемом периоде ограничены. Известны нормы расхода сырья 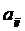; цены изделий 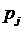; плановая себестоимость единицы изделия 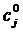. Известно также, что фактическая себестоимость единицы изделия отклоняется от плановой из-за несоответствия объемов выпуска мощности предприятия. Связь между фактической и плановой себестоимостью характеризуется следующим выражением:

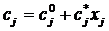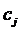, где - фактическая себестоимость, 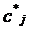- коэффициент отклонения фактической себестоимости от плановой, 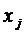- объем выпуска изделия.

Требуется: составить план выпуска двух изделий, максимизирующий прибыль предприятия.

Если использовать инструментальные переменные 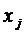для обозначения объемов выпуска изделий, то модель задачи будет иметь следующий вид:

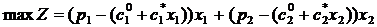
при ограничениях

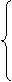
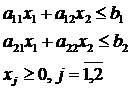
Наличие в модели всего лишь двух инструментальных переменных открывает возможность использовать для решения задачи метод, основанный на построении графической схемы. Схема должна отображать как область допустимых решений, так и целевую функцию задачи. Поскольку ограничения задачи линейны, способ отображения ОДР прост и очевиден. Однако для изображения целевой функции потребуется несколько видоизменить запись ее формулы.

Приведем формулу целевой функции к узнаваемому виду с помощью выделения полных квадратов двучлена относительно переменных 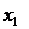и 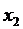. В формуле целевой функции проведем преобразования так, чтобы в результате уравнение целевой функции приняло вид:

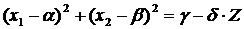, где 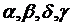- числа.

Стало очевидным, что мы располагаем записью уравнений окружностей с общим центром, имеющим координаты 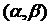. Данные окружности являются линиями уровня целевой функции задачи.

Строим графическую схему, нанося на координатную плоскость линии ограничений и линии уровня целевой функции. Цель графического анализа – определить приблизительное местонахождение точки оптимума.

На рисунке 9 приводится условная графическая схема задачи.

О

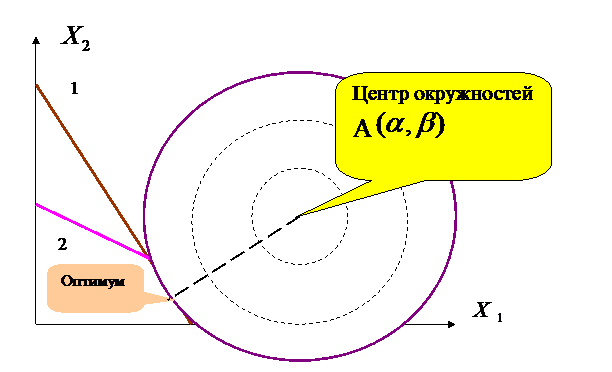
Рис. 9. Графическая схема задачи.

На основе схемы можно сделать вывод, что оптимальное решение нашей задачи принадлежит линии первого ограничения.

Для получения координат точки оптимума необходимо решить систему 2-х уравнений, одно из которых – уравнение линии первого ограничения, а другое – уравнение линии, проходящей через точку А и перпендикулярной линии первого ограничения. Первое уравнение известно, а второе необходимо вывести.

Для выведения второго уравнения запишем формулу пучка прямых, проходящих через точку А:

,

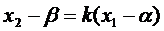где 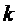– угловой коэффициент линии. Коэффициенты перпендикулярных прямых противоположны по знаку и обратны по величине, что позволяет определить значение 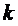. Найдем коэффициент линии первого ограничения, выражая 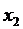через :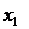

.

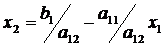Откуда получаем .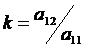

Составляем систему из двух уравнений, решением которой являются координаты точки оптимума. Подставив найденные значения 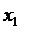и 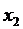в целевую функцию, мы определим ее максимальное значение.

3.2.2.Метод множителей Лагранжа.

Если ограничения задачи НЛП являются равенствами, то для ее решения можно использовать метод множителей Лагранжа. Основой метода является введение в решение вспомогательной функции Лагранжа. Функция Лагранжа образована двумя слагаемыми. Первое слагаемое – сама целевая функция, второе слагаемое – сумма произведений особых переменных 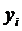(множителей Лагранжа) на разности .

.

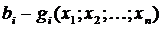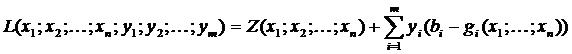Решение задачи основано на следующих действиях:

- определение частных производных функции Лагранжа по переменным 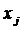и ;

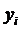- определение координат стационарных точек функции Лагранжа;

- анализ функции Лагранжа на выпуклость-вогнутость по переменным ;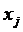

- получение выводов: вогнутость функции Лагранжа по переменным 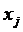означает, что в данной точке функция 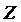достигает максимума на области допустимых решений задачи; выпуклость 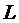означает, что в этой точке 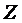достигает минимума на области допустимых решений задачи.

Для определения координат стационарных точек функции Лагранжа следует приравнять частные производные функции первого порядка к нулю и сформировать из данных уравнений систему. Решения данной системы и есть стационарные точки функции Лагранжа.

Рассмотрим применение метода на примере. Предположим, требуется найти 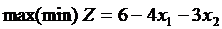при ограничении 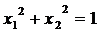без требования неотрицательности переменных.

Составим функцию Лагранжа:

.

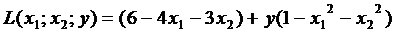Определим ее частные производные:

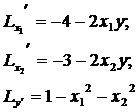
Найдем координаты стационарных точек функции 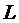путем решения следующей системы уравнений:

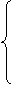
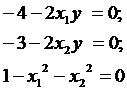
Решения данной системы:

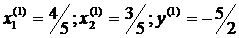и 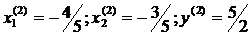. Они представляют собой координаты двух стационарных точек функции Лагранжа. Проведем анализ функции Лагранжа на выпуклость-вогнутость по переменным 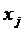с помощью вторых частных производных. Вторые частные производные по :

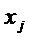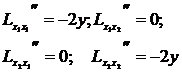. Составим из них матрицу 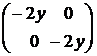. Определяем значения компонент матрицы в первой стационарной точке 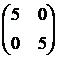. Выпуклость функции очевидна, поскольку 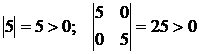. Таким образом, в первой стационарной точке целевая функция 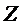достигает наименьшего значения на ОДР задачи. Определяем значения компонент матрицы во второй стационарной точке 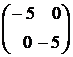. Очевидна вогнутость функции, так как 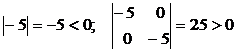. Таким образом, 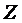во второй стационарной точке достигает максимального значения. Минимальное и максимальное значение целевой функции определяется путем подстановки в ее формулу значений 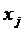в данных стационарных точках.

Метод, основанный на использовании множителей Лагранжа, достаточно распространен при решении задач нелинейного программирования.

3.3.3.Градиентный метод.

Наибольшей универсальностью при решении задач нелинейного программирования характеризуется градиентный метод. Градиентный метод основан на использовании градиента целевой функции и имеет различные модификации.

Рассмотрим основные шаги процедуры градиентного метода.

1. Выбираем в ОДР начальную точку .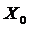

2. Записываем общее выражение градиента (или антиградиента) целевой функци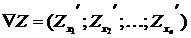и или .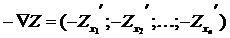

3. Определяем значение компонент градиента или антиградиента в точке .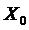

4. Записываем выражение для перехода в точку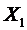

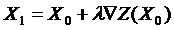
5. Для вычисления длины шага 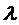записываем выражение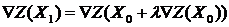

Вычисляем длину шага по уравнению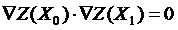

6. Находим координаты .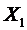

7. Находим 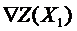или кратный ему вектор .

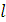8. Воспроизводим действия до тех пор, пока в очередной точке 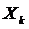градиент ( или антиградиент) функции не обращается в ноль .

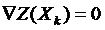Примечание. Необходимо проверить данную точку на принадлежность ОДР.

Последующие шаги характеризуют решение для случаев, когда оптимум находится не внутри ОДР, а на ее границе.

9. Возвращаемся на границу ОДР. С этой целью выясним, какому ограничению не удовлетворяет очередная точка 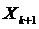. Из точки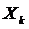

Мы попали в нее с помощью выражения 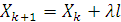. Для каждой отдельной координаты это выражение записываем в виде 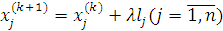. Очевидно, для возвращения на границу ОДР нам необходимо изменить длину шага 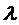.Запишем 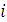-ое ограничение, которому не удовлетворяет точка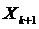

.

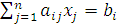Чтобы выйти на требуемую длину шага 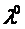перепишем выражение

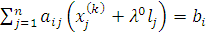. Откуда получим .

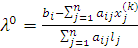Если таких ограничений несколько, то среди нескольких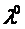

выбираем наименьшее.

10. Определяем 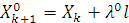. Данная точка принадлежит границе ОДР.

11. На границе ОДР определяем направление желательного изменения целевой функции. С этой целью возьмем в найденной точке 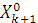производную по направлению .

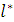12. Записываем выражение для точки оптимума 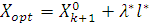, кроме того, воспользуемся вспомогательной записью 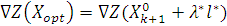. Для получения длины шага 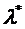используем уравнение .

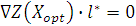13. Вычисляем координаты точки оптимума и экстремальное значение целевой функции.