Абсолютная и условная сходимость рядов

Рассмотрим произвольный знакопеременный ряд

U₁ + U₂ + ... + U_n + ... , (8.1)

т. е. ряд с членами произвольных знаков. Рассмотрим ряд, составленный из абсолютных величин членов ряда (8.1):

|U₁| + |U₂| + ... + |U_n| + ... , (8.2)

Теорема.

Если сходится ряд (8.2), то сходится и ряд (8.1).

Доказательство сразу получается из принципа сходимости : неравенство

|U_n+1 + U_n+2 + ... + U_n+m| £ |U_n+1| + |U_n+2| + ... + |U_n+m|

показывает, что если условие сходимости выполняется для ряда (8.2), то оно тем более выполняется для ряда (8.1).

Можно рассуждать иначе. Из положительных членов ряда (8.1), перенумеровав их по порядку, составим ряд

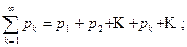(P),

так же поступим с отрицательными членами и составим ряд из их абсолютных величин

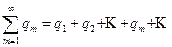(Q)

Сколько бы членов того или другого ряда ни взять, все они содержатся среди членов сходящегося ряда (8.2), и для всех частичных сумм Р_к и Q_m выполняется неравенства

Р_к £ S*; Q_m £ S*,

так что оба ряда (Р) и (Q) сходятся; обозначим их суммы соответсвенно, через Р и Q.

Если взять n членов ряда (А), то в их составе окажется k положительных и m отрицательных, так что

S_n = P_k - Q_m. (8.3)

Здесь номера k и m зависят от n. Если в ряде (8.1) как положительных, так и отрицательных членов бесчисленное множество, то при n®¥ одновременно k®¥ и m®¥.

Переходя в равенстве (8.3) к пределу, приходим снова к заключению о сходимости ряда (8.1), причем его сумма оказывается равной

S = P - Q.

Можно сказать, что при сделанных предположениях сумма данного ряда равна разности между суммой ряда, составленного из одних положительных его членов, и суммой ряда, составленного из абсолютных величин отрицательных членов.

Если ряд (8.1) сходится вместе с рядом (8.2), составленным из абсолютных величин его членов, то про ряд (8.1) говорят, что он абсолютно сходится.

Если ряд (8.1) сходится и ряд (8.2) расходится. Тогда ряд (8.1) называют условно сходящимся.

Между свойствами абсолютно и условно сходящихся рядов имеется глубокое различие.

Теорема.

Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов, причем сумма ряда не зависит от порядка его членов.

Если ряд сходится условно, то какое бы мы ни задали число А, или символ + ¥ или - ¥, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной А (или + ¥ или - ¥). Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки членов, окажется расходящимся.

На доказательство этой теоремы мы не будем останавливаться.

Приведем пример, показывающий, что сумма условно сходящегося ряда меняется при перестановке его членов.

Рассмотрим условно сходящийся ряд

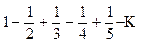(8.3)

Переставим его члены так, чтобы после одного положительного члена шло два отрицательных. Получим ряд

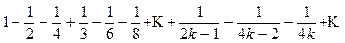(8.4)

Обозначим через S сумму данного ряда, покажем, что сумма полученного ряда равна 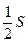. Обозначим через S_n и s_n частичные суммы рядов (8.3) и (8.4) и рассмотрим частичную сумму s_n при n = 3k.

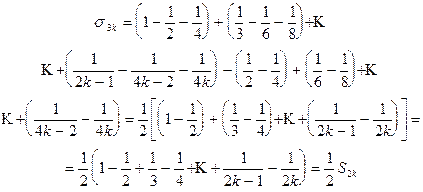
Следовательно, .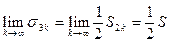

Далее замечаем, что

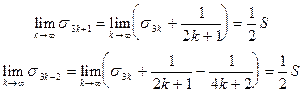
Таким образом, .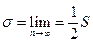

Итак, доказано, что в результате перестановки членов ряда его сумма изменилась (она вдвое уменьшилась).

Этот вывод, который на первый взгляд кажется парадоксальным, говорит о том, что бесконечные ряды отличаются по своим свойствам от сумм конечного числа слагаемых.