Дифференциальное уравнение теплопроводности

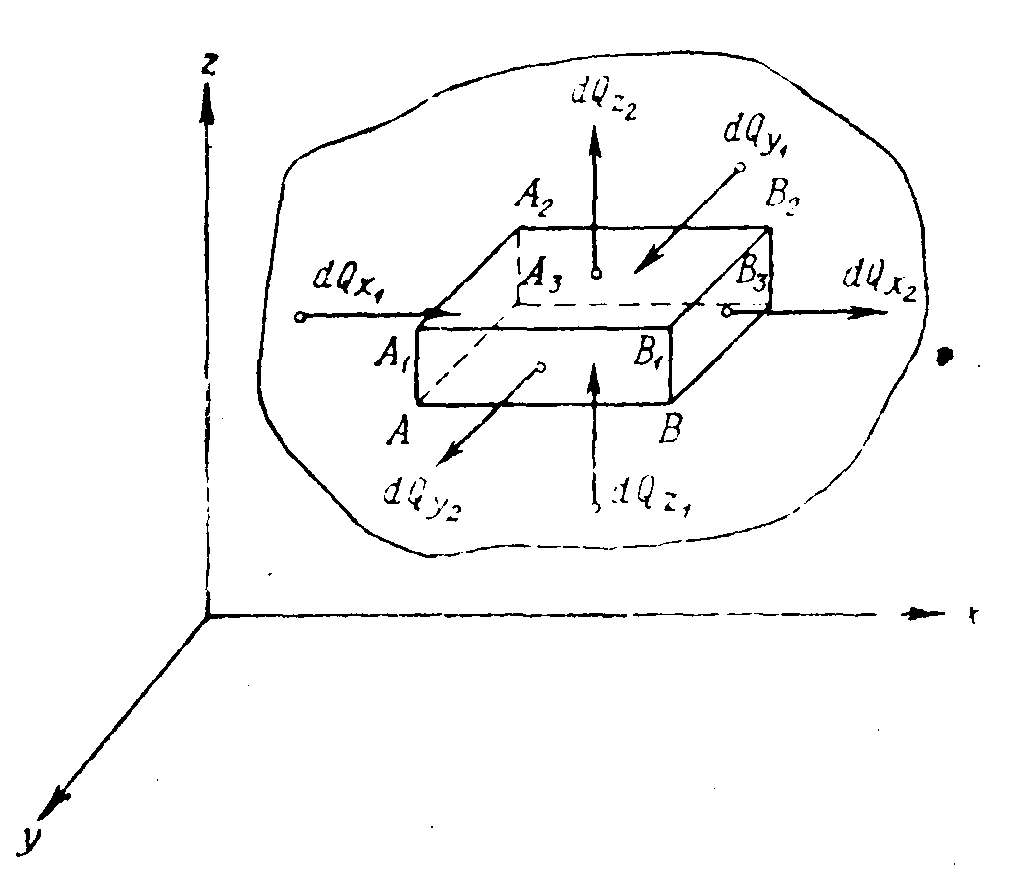
При решении всех без исключения задач теплопроводности как при стационарном, так и при нестационарном тепловом режимах, обязательным является знание поля температур.

При выводе дифференциального уравнения теплопроводности бу­дем считать, что физические параметры: l (коэффициент тепло­проводности), с (теплоемкость) и g (удельный вес) не зависят от координат и времени в пределах всего поля.

.

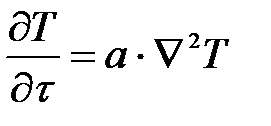Уравнение называется основным дифференциальным уравнением теплопроводности.

Оно устанавливает связь между временным и пространственным изменением температуры в любой точке поля.

Величина

.

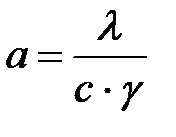называется коэффициентом температуропроводности тела.

Краевые условия. Расчетное уравнение теплоотдачи

Основное дифференциальное уравнение теплопроводности характеризует пространственно-временное изменение температуры в любой точке поля, объединяя все без исключения явления теплопроводности независимо от геометрической формы тела, его физических свойств и условий взаимодействия с окружающей средой.

Краевые граничные условия связаны с взаимодействием изучаемого тела с окружающей средой (например, распределение температур на поверхности тела для каждого момента времени). Граничные краевые условия в свою очередь могут быть заданы тремя способами:

1. Граничное условие первого рода задается распределением температур по поверхности тела для любого момента времени.

2. Граничное условие второго рода задается тепловым потоком в каждой точке поверхности тела для каждого момента времени.

3. Граничное условие третьего рода заключается в задании температуры среды, окружающей изучаемое тело, и закона теплоотдачи между поверхностями и окружающей средой.

Глава 2. ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ И ГРАНИЧНЫХ УСЛОВИЯХ ПЕРВОГО РОДА

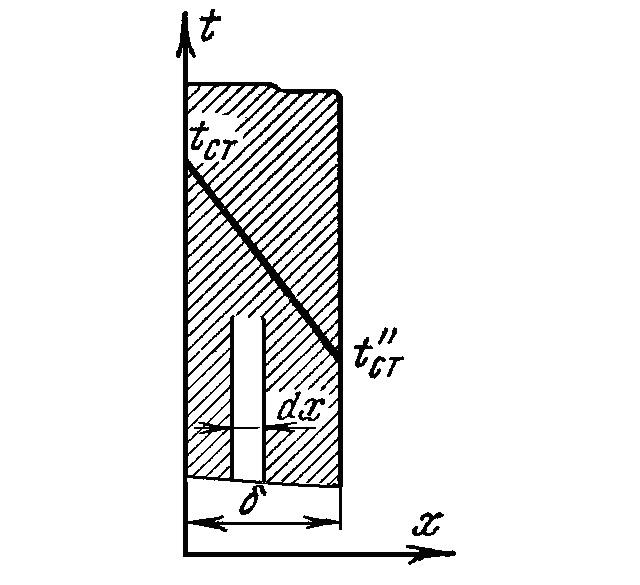
Теплопроводность через однослойную плоскую стенку

Дифференциальное уравнение теплопроводности позволяет опре­делить температуру в зависимости от времени и координат в любой точке поля.

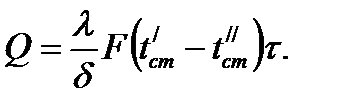
Количество теплоты, передаваемое теплопроводностью через пло­скую стенку, прямо пропорционально коэффициенту теплопровод­ности стенки 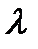ее площади 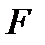, промежутку времени 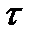, разности темпе­ратур на наружных поверхностях стенки 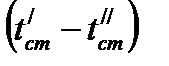и обратно про­порционально толщине стенки .

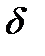Тепловой поток зависит не от абсо­лютного значения температур, а от их разности 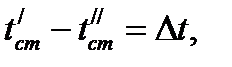на­зываемой температурным напором.