Применение производной при решении неравенств
ВСТУПЛЕНИЕ
Элементы математического анализа занимает значительное место в школьном курсе математики. Учащиеся овладевают математическим аппаратом, который может быть эффективно использован при решении многих задач математики, физики, техники. Язык производной и интеграла позволяет строго формулировать многие законы природы. В курсе математики с помощью дифференциального и интегрального исчислений исследуются свойства функций, строятся их графики, решаются задачи на наибольшее и наименьшее значения, вычисляются площади и объемы геометрических фигур. Иными словами, введение нового математического аппарата позволяет рассмотреть ряд задач, решить которые нельзя элементарными методами. Однако возможности методов математического анализа такими задачами не исчерпывается.
Многие традиционные элементарные задачи (доказательство неравенств, тождеств, исследование и решение уравнений и другие) эффективно решаются с помощью понятий производной и интеграла. Школьные учебники и учебные пособия мало уделяют внимания этим вопросам. Вместе с тем нестандартное использование элементов математического анализа позволяет глубже усвоить основные понятия изучаемой теории. Здесь приходится подбирать метод решения задачи, проверять условия его применимости, анализировать полученные результаты. По существу, зачастую проводится небольшое математическое исследование, в процессе которого развиваются логическое мышление, математические способности, повышается математическая культура.
Для многих задач элементарной математики допускается как «элементарное», так и «неэлементарное» решение. Применение производной и интеграла дает как правило более эффективно решение. Появляется возможность оценить силу, красоту, общность нового математического аппарата.
Методы математического анализа используются не только для решения поставленных задач, но и являются источником получения новых фактов элементарной математики.
РАЗДЕЛ 1
НЕКОТОРЫЕ ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ
Применение производной при решении неравенств
Дифференциальное исчисление широко используется при исследовании функций. С помощью производной можно найти промежутки монотонности функции, ее экстремальные точки, наибольшие и наименьшие значения.
Если функция 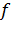 положительную (отрицательную) производную в каждой точке некоторого промежутка, то она возрастает (убывает) на этом промежутке. При нахождении промежутков монотонности нужно иметь в виду, что если функция возрастает (убывает) на интервале
положительную (отрицательную) производную в каждой точке некоторого промежутка, то она возрастает (убывает) на этом промежутке. При нахождении промежутков монотонности нужно иметь в виду, что если функция возрастает (убывает) на интервале 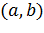 и непрерывна в точках
и непрерывна в точках 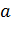 и
и 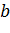 , то она возрастает (убывает) на отрезке
, то она возрастает (убывает) на отрезке 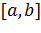 .
.
Если точка 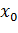 является точкой экстремума для функции
является точкой экстремума для функции 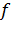 и в этой точке существует производная, то
и в этой точке существует производная, то 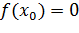 . В точке экстремума функция может не иметь производную. Внутренние точки области определения, в которых производная равна нулю или не существует, называются критическими. Чтобы установить, имеет ли функция в данной критической точке экстремум, пользуются следующими достаточными признаками существования экстремума.
. В точке экстремума функция может не иметь производную. Внутренние точки области определения, в которых производная равна нулю или не существует, называются критическими. Чтобы установить, имеет ли функция в данной критической точке экстремум, пользуются следующими достаточными признаками существования экстремума.
Если функция 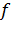 непрерывна в точке
непрерывна в точке 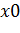 и существуют такие точки
и существуют такие точки 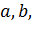 что
что 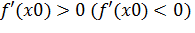 на интервале
на интервале 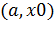 и
и 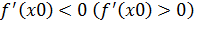 на интервале
на интервале 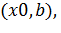 то точка
то точка 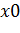 является точкой максимума (минимума) функции
является точкой максимума (минимума) функции 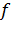 .
.
Для отыскания наибольших и наименьших значений 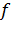 на отрезке
на отрезке 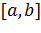 достаточно сравнить между собой значения
достаточно сравнить между собой значения 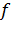 в точках
в точках  и в критических точках из отрезка
и в критических точках из отрезка 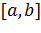 .
.
Эти результаты применимы при решении многих элементарных задач, связанных с неравенствами.
Пусть, например, требуется доказать, что на некотором промежутке имеет место неравенство 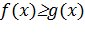 . Обозначим
. Обозначим 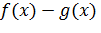 через
через 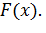 С помощью производной
С помощью производной 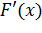 находим наименьшее значение
находим наименьшее значение 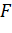 на данном промежутке. Если оно неотрицательно, то во всех точках рассматриваемого промежутка
на данном промежутке. Если оно неотрицательно, то во всех точках рассматриваемого промежутка 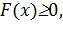 т.е.
т.е. 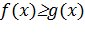 .
.
Задача 1.1.Доказать что 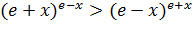 для
для 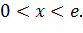
Решение.
Данное неравенство равносильно следующему:
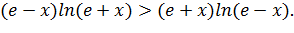
Пусть 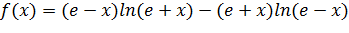 ,
,
тогда 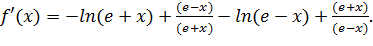
Так как 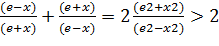 ,
,
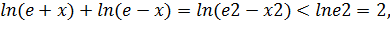
то 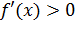 при
при 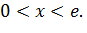 Следовательно, функция
Следовательно, функция 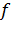 возрастает на интервале
возрастает на интервале 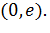 Функция
Функция 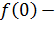 непрерывна. Поэтому эту точку можно включить в промежуток возрастания. Поскольку
непрерывна. Поэтому эту точку можно включить в промежуток возрастания. Поскольку 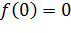 , а
, а 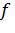 возрастает при
возрастает при 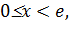 то
то 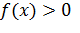 при
при 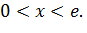 Отсюда получаем решение задачи 1.
Отсюда получаем решение задачи 1.
Задача 1.2.Два туриста отправились по одному маршруту. В первый день они прошли одно и то же расстояние. В каждый из следующих дней первый турист увеличивал пройденный путь, по сравнению предыдущим, на одно и то же расстояние, а второй – в одно и то же число раз. Выяснилось, что в 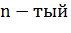 день
день 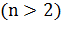 путешествия туристы снова прошли одно и то же расстояние. Доказать, что за
путешествия туристы снова прошли одно и то же расстояние. Доказать, что за 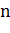 дней первый турист прошел путь больший, чем второй.
дней первый турист прошел путь больший, чем второй.
Решение.
Расстояние, пройденное первым туристом за 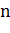 дней, представляет собой сумму
дней, представляет собой сумму 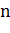 первых членов арифметической прогрессии, а вторым – сумму
первых членов арифметической прогрессии, а вторым – сумму 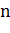 первых членов геометрической прогрессии. Обозначим эти расстояния соответственно
первых членов геометрической прогрессии. Обозначим эти расстояния соответственно 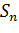 и
и 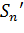 . Если
. Если  первый член прогрессии,
первый член прогрессии, 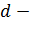 разность арифметической прогрессии,
разность арифметической прогрессии, 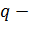 знаменатель геометрической прогрессии, то
знаменатель геометрической прогрессии, то
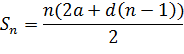
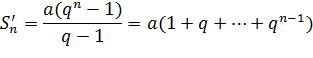
Приравнивая 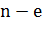 члены прогрессий, находим
члены прогрессий, находим
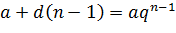
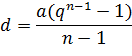
Тогда 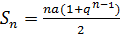 , где
, где 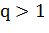 (по условию задачи). Задача 4 будет решена, если мы покажем, что
(по условию задачи). Задача 4 будет решена, если мы покажем, что 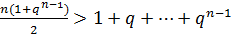 где
где 
При 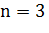 имеем
имеем 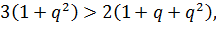 равносильно очевидному неравенству
равносильно очевидному неравенству 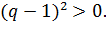 Предполагая, что неравенство (2) справедливо при
Предполагая, что неравенство (2) справедливо при 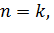 докажем его для
докажем его для 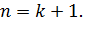 Имеем
Имеем

Для завершения доказательства достаточно убедиться, то выражение
 при
при 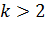 . Здесь целесообразно обратиться к производной.
. Здесь целесообразно обратиться к производной.
Пусть 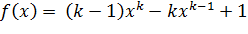
Производная 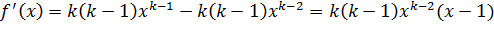 положительная при
положительная при  Поэтому
Поэтому 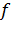 при
при 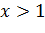 возрастает. Так как
возрастает. Так как 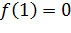 и функция
и функция 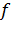 непрерывна в точке
непрерывна в точке 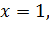 то
то  при
при 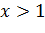 т.е.
т.е.  Итак,
Итак, 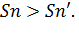 Задача 2 решена.
Задача 2 решена.
