Кривые второго порядка на плоскости
К кривым второго порядка относятся парабола, гипербола, эллипс(частный случай эллипса – окружность).Любая кривая второго порядка в общем виде описывается уравнением второй степени с двумя переменными:
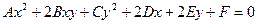 (1)
(1)
Коэффициенты 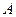 ,
, 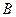 и
и 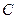 не равны нулю одновременно.
не равны нулю одновременно.
Парабола
Параболойназывается множество всех точек, расстояния которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, равны.
Каноническими уравнениями параболы являются:
1) 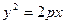 , где
, где 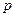 - параметр параболы, расстояние от фокуса до директрисы, для кривой с горизонтально расположенной осью; 2)
- параметр параболы, расстояние от фокуса до директрисы, для кривой с горизонтально расположенной осью; 2) 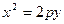 - для параболы с вертикально расположенной осью.
- для параболы с вертикально расположенной осью.
Пример 1. Рассмотрим параболу 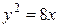 . Для неё
. Для неё 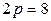 , т.е.
, т.е. 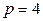 ; осью параболы является ось
; осью параболы является ось 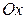 (в уравнении параболы переменная
(в уравнении параболы переменная 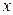 в первой степени); ветви параболы направлены вправо (так как
в первой степени); ветви параболы направлены вправо (так как 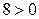 ).
).
Для построения кривой второго порядка в Excel в уравнении кривой выражают 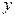 через
через 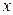 :
: 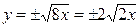 , откуда следует, что
, откуда следует, что 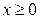 . Это определяет диапазон изменения аргумента
. Это определяет диапазон изменения аргумента 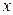 , т.е. можно взять
, т.е. можно взять 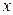 , например от 0 до 6.
, например от 0 до 6.
Пример 2. Рассмотрим параболу 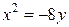 . Имеем
. Имеем 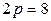 , т.е.
, т.е. 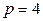 ; осью параболы является ось
; осью параболы является ось 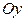 (в уравнении параболы переменная
(в уравнении параболы переменная 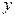 в первой степени); ветви параболы направлены вниз (так как
в первой степени); ветви параболы направлены вниз (так как 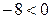 ).
).
Выражаем 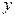 через
через 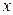 :
: 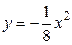 , откуда ясно, что
, откуда ясно, что 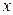 - любое число. Поэтому в данном случае диапазон изменения
- любое число. Поэтому в данном случае диапазон изменения 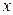 берём симметрично относительно начала координат, например, от -5 до +5.
берём симметрично относительно начала координат, например, от -5 до +5.
Гипербола
Гиперболой называется множество точек плоскости, разность расстояний от которых до двух данных точек 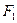 и
и 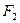 , называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами. Каноническое уравнение гиперболы имеет вид:
, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами. Каноническое уравнение гиперболы имеет вид:
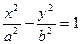 ,
, 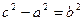 ,
, 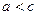
или 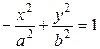 ,
, 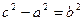 ,
, 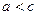 .
.
Здесь 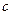 - расстояние от начала координат до фокусов, а - расстояние от начала координат до вершин гиперболы.
- расстояние от начала координат до фокусов, а - расстояние от начала координат до вершин гиперболы.
В простейшем случае уравнение гиперболы имеет вид
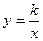 .
.
Пример 3. Рассмотрим гиперболу 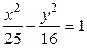 .
.
1. Заметим, что в уравнении гиперболы перед 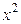 подразумевается знак «+», а перед
подразумевается знак «+», а перед 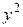 стоит знак «-», это означает, что ось
стоит знак «-», это означает, что ось 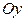 является мнимой осью (гипербола не пересекает мнимую ось), а ось
является мнимой осью (гипербола не пересекает мнимую ось), а ось 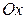 является действительной осью гиперболы (гипербола пересекает действительную ось в двух точках
является действительной осью гиперболы (гипербола пересекает действительную ось в двух точках 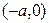 ,
, 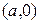 - вершинах гиперболы). Полуоси гиперболы находим следующим образом:
- вершинах гиперболы). Полуоси гиперболы находим следующим образом: 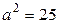 , откуда, так как
, откуда, так как 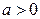 имеем, что
имеем, что 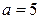 ;
; 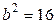 , откуда, так как
, откуда, так как 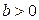 имеем
имеем 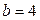 .
.
2. Выразим 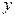 через
через 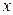 в уравнении гиперболы:
в уравнении гиперболы: 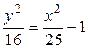 ,
, 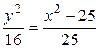 ,
, 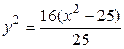 ,
, 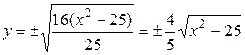 .
.
3. На основании этого определим диапазон изменения 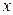 , т.е. найдём область определения полученной функции:
, т.е. найдём область определения полученной функции: 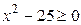 ,
, 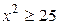 ,
, 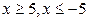 . Это означает, что правую ветвь гиперболы надо строить в диапазоне
. Это означает, что правую ветвь гиперболы надо строить в диапазоне 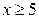 (т.е.
(т.е. 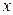 брать от 5 до, например, 8), а левую -
брать от 5 до, например, 8), а левую - 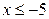 (т.е.
(т.е. 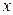 брать от -8 до -5).
брать от -8 до -5).
Пример 4. Рассмотрим гиперболу 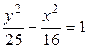 .
.
1. Заметим, что в уравнении гиперболы перед 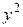 подразумевается знак «+», а перед
подразумевается знак «+», а перед 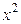 стоит знак «-», это означает, что ось
стоит знак «-», это означает, что ось 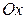 является мнимой осью (гипербола не пересекает мнимую ось), а ось
является мнимой осью (гипербола не пересекает мнимую ось), а ось 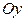 является действительной осью гиперболы (данная гипербола пересекает действительную ось в двух точках
является действительной осью гиперболы (данная гипербола пересекает действительную ось в двух точках 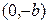 ,
, 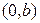 - вершинах гиперболы).
- вершинах гиперболы).
Полуоси гиперболы: 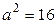 , откуда ,, откуда
, откуда ,, откуда 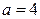 ,
, 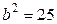 , откуда
, откуда 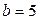 .
.
2. Выразим 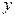 через
через 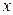 в уравнении гиперболы:
в уравнении гиперболы: 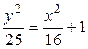 ,
, 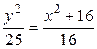 ,
, 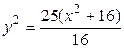 ,
, 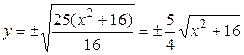 .
.
3. Определим диапазон изменения 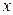 , т.е. найдём область определения полученной функции. В данном случае
, т.е. найдём область определения полученной функции. В данном случае 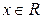 . Поэтому при построении данной гиперболы
. Поэтому при построении данной гиперболы 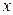 можно взять в диапазоне, например, от -5 до 5.
можно взять в диапазоне, например, от -5 до 5.
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек (эта сумма обозначается 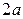 ), называемых фокусами, есть величина постоянная, большая расстояния
), называемых фокусами, есть величина постоянная, большая расстояния 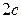 между фокусами. Каноническое уравнение эллипса имеет вид:
между фокусами. Каноническое уравнение эллипса имеет вид: 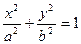 (здесь
(здесь 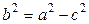 ).
).
Так как 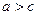 , то
, то 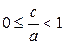 , т.е. эксцентриситет эллипса находится в пределах
, т.е. эксцентриситет эллипса находится в пределах 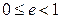 .
.
Пример 5. Рассмотрим эллипс 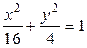 .
.
1. Так как 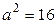 ,
, 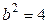 , то его полуоси равны
, то его полуоси равны 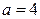 ,
, 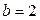 . Это означает, что все точки эллипса имеют абсциссы в диапазоне
. Это означает, что все точки эллипса имеют абсциссы в диапазоне 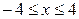 , а ординаты в диапазоне
, а ординаты в диапазоне 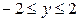 .
.
2. Выразим 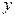 через
через 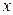 в уравнении эллипса:
в уравнении эллипса: 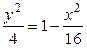 ,
, 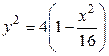 ,
, 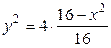 ,
, 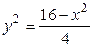 , откуда
, откуда 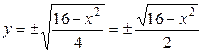 .
.
3. Находим область определения полученной функции: 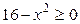 ,
, 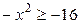 ,
, 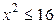 ,
, 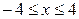 , что было получено выше.
, что было получено выше.
Окружность
Окружность является частным случаем эллипса, а именно это эллипс с равными полуосями.
Окружностьюназывается множество точек плоскости, находящихся на одинаковом расстоянии от данной точки, называемой центром.
Каноническое уравнение окружности имеет вид: 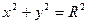 - уравнение окружности с центром в начале координат и радиусом R,
- уравнение окружности с центром в начале координат и радиусом R, 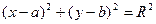 - уравнение окружности радиуса
- уравнение окружности радиуса 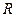 с центром
с центром 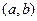 .
.
 Для построения кривых второго порядка в MS Excel их уравнения должны быть предварительно приведены к виду
Для построения кривых второго порядка в MS Excel их уравнения должны быть предварительно приведены к виду 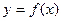 (т.е. разрешены относительно переменной у).
(т.е. разрешены относительно переменной у).
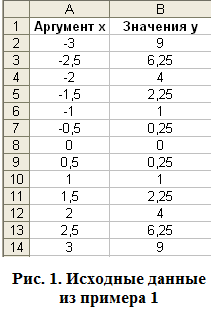
Пример 6.Построение параболы вида 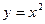 в диапазоне
в диапазоне 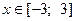 с шагом
с шагом 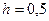 .
.
1. Ввод данных. На Листе1 составьте таблицу данных (х и у), как показано на рисунке 1.
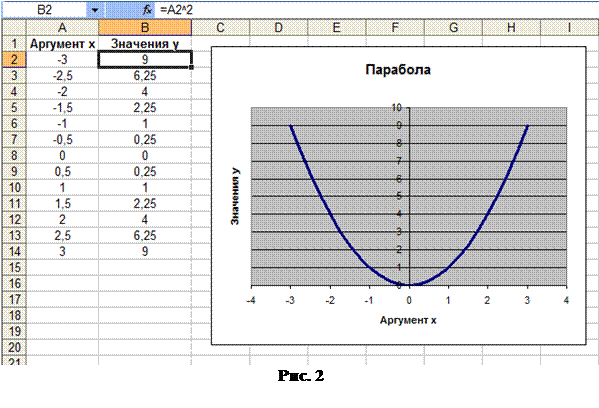
2. Построение диаграммы (графика). Вызвать Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указать тип диаграммы: Точечная, вид - вторая диаграмма во втором ряду. Перейти ко второму шагу Мастера диаграмм, нажав кнопку Далее. В рабочем поле Диапазон данныхустановить курсор и левой кнопкой мыши выделить диапазон В2:В14 на Листе1 Excel. После чего в поле Диапазон данных появится: =Лист1!$В$2:$В$14. Переключатель Ряды в с помощью указателя мыши следует установить в положение столбцах.Затем перейти на вкладкуРяд.В полеЗначения хустановить курсор и левой кнопкой мыши выделить диапазонА2:А14.Нажав кнопку Далее перейти к шагу 3. Здесь на вкладке Заголовки вводятся название диаграммы и осей. Остальные вкладки можно не трогать. Следующий шаг Мастера диаграмм выполните самостоятельно, чтобы получилось так, как показано на рисунке 2. Дважды нажав кнопкой мыши на полученном графике можно изменить толщину линий, их цвет и другие параметры (изучите самостоятельно).
Пример 7.Построение параболы вида 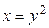 в диапазоне
в диапазоне 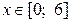 с шагом
с шагом 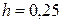 .
.
Для этого необходимо в уравнении параболы выразить 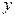 через
через 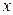 :
: 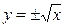 . Поэтому искомый график будет состоять из двух кусков: первый лежит выше оси
. Поэтому искомый график будет состоять из двух кусков: первый лежит выше оси 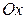 (значения
(значения 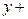 ), второй – ниже оси
), второй – ниже оси 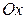 (значения
(значения 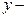 ).
).
1. Ввод данных. На Листе2 составьте таблицу данных (х и у), как показано на рисунке 1. При этом в ячейку В2 заносим формулу «=КОРЕНЬ(А2)», а в ячейку С2 – формулу «=- КОРЕНЬ(А2)» или «= - В2».
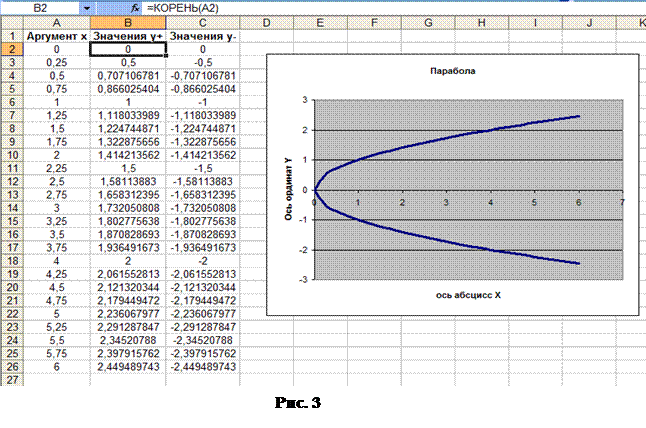
2. Построение диаграммы (графика). Вызвать Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указать тип диаграммы: Точечная, вид - вторая диаграмма во втором ряду. Перейти ко второму шагу Мастера диаграмм, нажав кнопку Далее. В рабочем поле Диапазон данныхустановить курсор и левой кнопкой мыши выделить диапазон В2:В26 на Листе2 Excel. После чего в поле Диапазон данных появится: =Лист2!$В$2:$В$26. Переключатель Ряды в с помощью указателя мыши следует установить в положение столбцах.Затем перейти на вкладкуРяд.В полеЗначения хустановить курсор и левой кнопкой мыши выделить диапазонА2:А26. Слева в полеРяднажать кнопкуДобавить. Справа установить курсор в полеЗначения Х:и левой кнопкой мыши выделить диапазонА2:А26.В полеЗначения Y:установить курсор и выделить левой кнопкой мыши диапазонС2:С26.Нажав кнопку Далее перейти к шагу 3. Здесь на вкладке Заголовки вводятся название диаграммы и осей. Остальные вкладки можно не трогать. Закончите выполнение шагов Мастера диаграмм. Дважды нажав кнопкой мыши на каждом из полученных кусков графика, сделайте одинаковым цвет и толщину линий.
Пример 8. Построение гиперболы 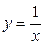 в диапазоне
в диапазоне 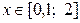 с шагом
с шагом 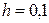 .
.
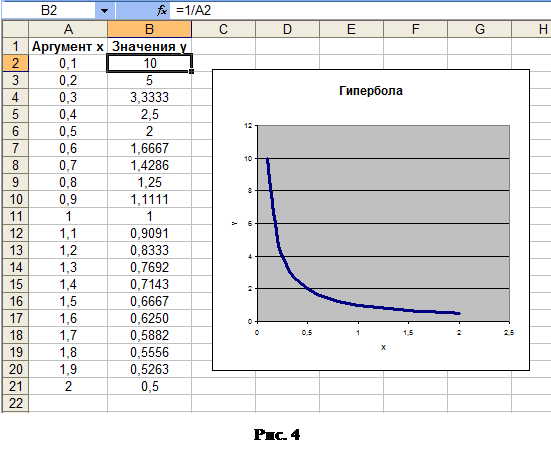 |
. 1. Ввод данных. На Листе3 составьте таблицу данных (х и у), как показано на рисунке 4.
2. Построение диаграммы (графика). Вызвать Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указать тип диаграммы: Точечная, вид – второй во втором ряду. В рабочем поле Диапазон указать диапазон: =Лист3!$А$2:$А$21. Переключатель Ряды в с помощью указателя мыши следует установить в положение столбцах.И затем нажать кнопку Далее в диалоговом окне. Последующие шаги Мастера диаграмм выполните самостоятельно, чтобы получилось так, как показано на рисунке 4.
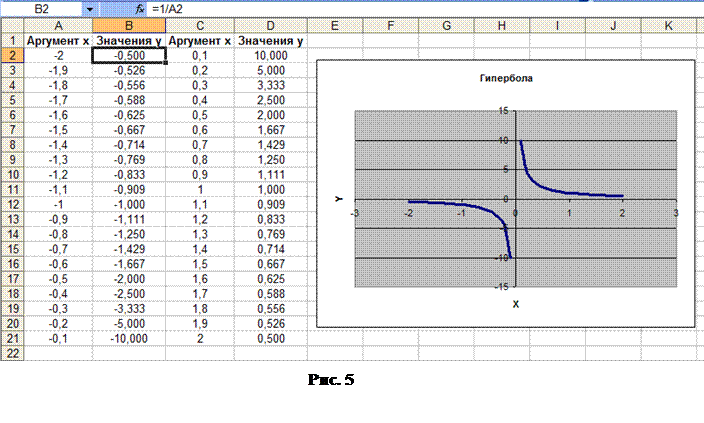
Задание.Внимательно изучив содержимое рисунка 5, выполните построение гиперболы 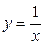 в указанных там диапазонах.
в указанных там диапазонах.
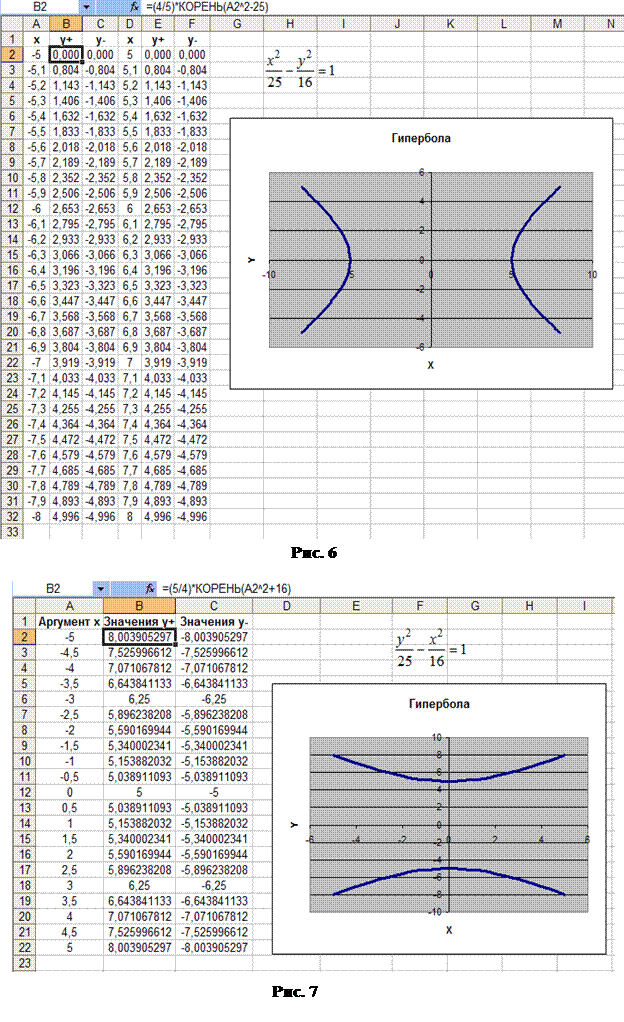
Пример 9. Построение гиперболы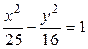 (см. пример 3).
(см. пример 3).
Выполните построение гиперболы, используя данные рисунка 6. Отметим, что в данном случае получается 4 ряда данных.
Пример 5.Построение гиперболы 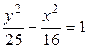 (см. пример 4).
(см. пример 4).
Выполните построение гиперболы, используя данные рисунка 7. Отметим, что в данном случае получается 2 ряда данных, которым соответствует верхняя и нижняя ветви гиперболы.
Пример 6.Построение верхней полуокружности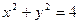 .
.
1. Выразим 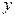 через
через 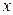 в уравнении окружности:
в уравнении окружности: 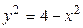 ,
, 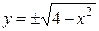 . Верхней полуокружности отвечают положительные значения
. Верхней полуокружности отвечают положительные значения 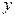 , т.е. берём
, т.е. берём 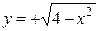 .
.
2. Определим диапазон изменения 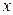 , т.е. найдём область определения полученной функции:
, т.е. найдём область определения полученной функции: 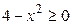 ,
, 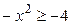 ,
, 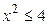 ,
, 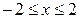 .
.
3. Выполните построение верхней полуокружности, используя данные рисунка 8.
Задание. Постройте окружность из примера 6.
 |
Задания для самостоятельной работы
1. Постройте гиперболы (рассчитайте диапазон, шаг выберите самостоятельно):
1. 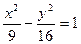 ,
, 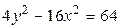 ,
, 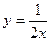
2. 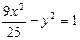 ,
, 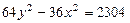 ,
, 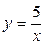
3. 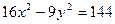 ,
, 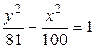 ,
, 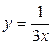
4. 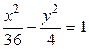 ,
, 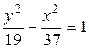 ,
, 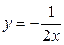
5. 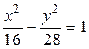 ,
, 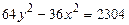 ,
, 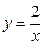
6. 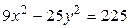 ,
, 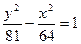 ,
, 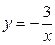
7. 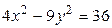 ,
, 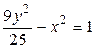 ,
, 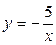
8. 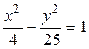 ,
, 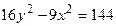 ,
, 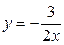
9. 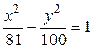 ,
, 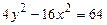 ,
, 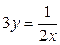
10. 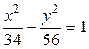 ,
, 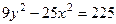 ,
, 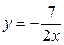
11. 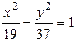 ,
, 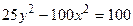 ,
, 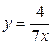
12. 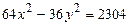 ,
, 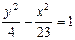 ,
, 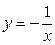
13. 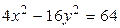 ,
, 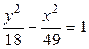 ,
, 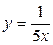
2. Постройте эллипсы (рассчитайте диапазон, шаг выберите самостоятельно):
1. 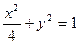
2. 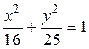
3. 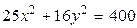
4. 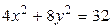
5. 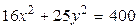
6. 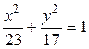
7. 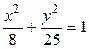
8. 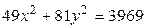
9. 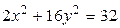
10. 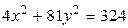
11. 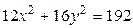
12. 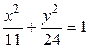
13. 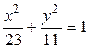
3. Постройте параболы (рассчитайте диапазон, шаг выберите самостоятельно):
1. 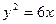 , , 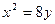 2. 2. 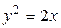 , , 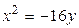 3. 3. 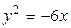 , , 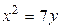 4. 4. 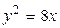 , , 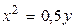 5. 5. 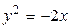 , , 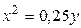 6. 6. 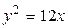 , , 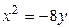 7. 7. 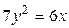 , , 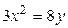 | 8. 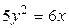 , , 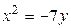 9. 9. 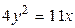 , , 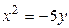 10. 10. 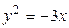 , , 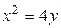 11. 11. 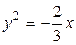 , , 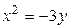 12. 12. 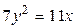 , , 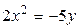 13. 13. 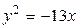 , , 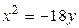 |
