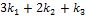Линейное векторное пространство
Линейное векторное пространство 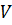 - это множество векторов, которые удовлетворяют двум условиям:
- это множество векторов, которые удовлетворяют двум условиям:
· сумма двух произвольных векторов x и y из множества V также является вектором, принадлежащим этому множеству;
· вектор, полученный умножением вектора из множества V на любой скаляр  , также принадлежит этому множеству.
, также принадлежит этому множеству.
При этом правила сложения векторов и умножения их на скаляр обладают следующими свойствами:
1) 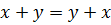 (коммутативность);
(коммутативность);
2) 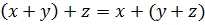 (ассоциативность);
(ассоциативность);
3) 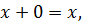 где 0 – нулевой вектор;
где 0 – нулевой вектор;
4) для любого вектора x существует такой вектор y, что 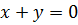 , где вектор
, где вектор 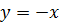 называют обратным вектору x;
называют обратным вектору x;
5) 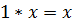 для любого x;
для любого x;
6) 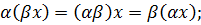 где α и β – скаляры;
где α и β – скаляры;
7) 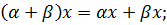
8) 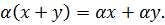
Наиболее простым примером линейного векторного пространства является множество векторов, принадлежащее трёхмерному Евклидову пространству.
Если системы векторов 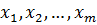 принадлежит пространству V, то множество векторов y, являющихся линейной комбинацией этих векторов, т.е.
принадлежит пространству V, то множество векторов y, являющихся линейной комбинацией этих векторов, т.е.
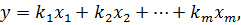 (3.10)
(3.10)
также образует векторное пространство. Размерность этого пространства равна числу его линейно независимых векторов.
Если только 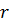 векторов x; в уравнении (3.10) является линейно независимыми, то размерность пространства, которое можно образовать этими векторами, равна
векторов x; в уравнении (3.10) является линейно независимыми, то размерность пространства, которое можно образовать этими векторами, равна 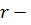 рангу системы векторов
рангу системы векторов 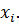
Например, имеется система векторов
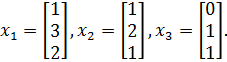
Эти векторы линейно зависимы, т.к. 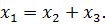 В этом случае
В этом случае 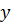 вектор равен:
вектор равен: 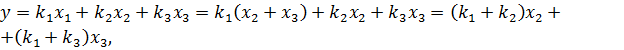 т.е. размерность векторного пространства равна двум (
т.е. размерность векторного пространства равна двум ( 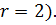
Если в 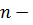 мерном пространстве
мерном пространстве 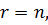 то систему n линейно независимых векторов называют часто линейной оболочкой. Её можно использовать в качестве базиса векторного пространства.
то систему n линейно независимых векторов называют часто линейной оболочкой. Её можно использовать в качестве базиса векторного пространства.
Базисом пространства называется такая система векторов, через которую единственным образом выражается произвольный вектор данного пространства. Базис, по существу, представляет систему координат.
Если заданы составляющие вектора 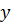 , то необходимо также указать базис или систему координат, по отношению к которой указаны эти составляющие. Например, расположение точки в трёхмерном пространстве может задаваться в прямоугольной системе координат, цилиндрической системе координат, сферической системе координат и т.д. Утверждение, что вектор
, то необходимо также указать базис или систему координат, по отношению к которой указаны эти составляющие. Например, расположение точки в трёхмерном пространстве может задаваться в прямоугольной системе координат, цилиндрической системе координат, сферической системе координат и т.д. Утверждение, что вектор
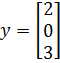
имеет составляющие 2, 0, 3 не имеет смысла, если не указан базис векторного пространства.
Пример 3.8. В ортогональном базисе (1, 0, 0), (0, 1, 0), (0, 0, 1) заданы три вектора 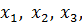 приведённые в примере 3.7. Необходимо представить в этом базисе вектор
приведённые в примере 3.7. Необходимо представить в этом базисе вектор 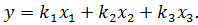
Следует сначала отметить, что если векторы 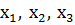 взять за базис, то вектор
взять за базис, то вектор 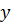 будет иметь следующий вид
будет иметь следующий вид
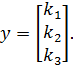
В заданном ортогональном базисе имеем:
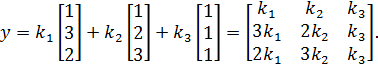
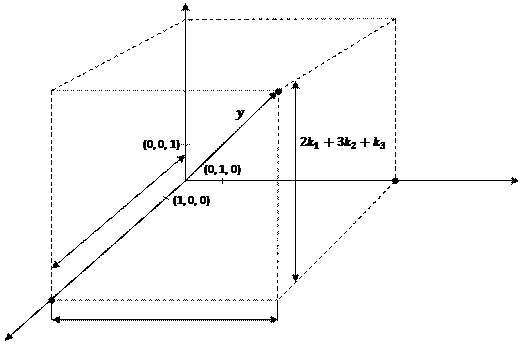 Результирующий вектор представлен на рис. 3.1.
Результирующий вектор представлен на рис. 3.1.
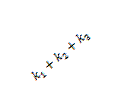
|
Рис. 3.1.