Преобразование координат точки и вектора
Рассмотрим какую-либо точку пространства 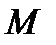 с координатами в старой системе:
с координатами в старой системе: 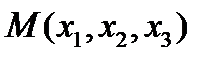 . Разложим радиус-вектор этой точки
. Разложим радиус-вектор этой точки 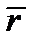 по старому базису:
по старому базису:
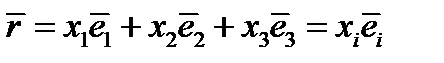 (24)
(24)
Перейдем в новую систему координат. Точка 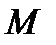 и ее радиус-вектор будут иметь уже новые координаты
и ее радиус-вектор будут иметь уже новые координаты 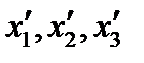 , и разложение
, и разложение 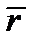 по новому базису будет выглядеть так:
по новому базису будет выглядеть так:
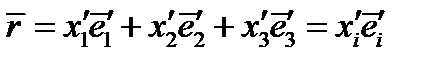 (25)
(25)
Подставим в формулу (24) формулы (20), выражающие старые базисные векторы через новые:
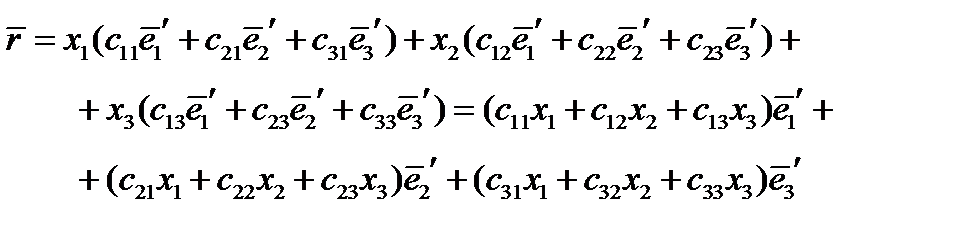
Пользуясь правилом Эйнштейна, запишем это короче:
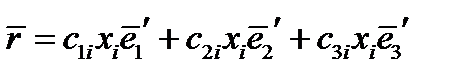 (26)
(26)
Сравнивая (26) с (25) и принимая во внимание, что разложение по базису единственно, получим, что координаты точки  в новой системе координат равны:
в новой системе координат равны:
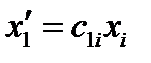 ,
, 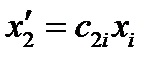 ,
, 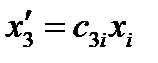 .
.
Эти формулы можно объединить в одну и тогда получим:
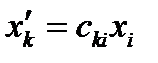 (27)
(27)
По этому правилу преобразуются координаты точки и радиус-вектора при переходе от старой системы координат к новой. Выведем теперь формулы обратного преобразования. Подставим в формулу (25) формулу (22а). При этом сразу будем пользоваться правилом суммирования:
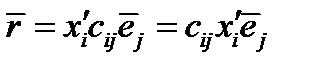 (28)
(28)
Сравним (28) с (24). При этом, поскольку в (24) индекс 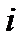 является немым, заменим его буквой
является немым, заменим его буквой 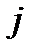 , а в (28) немой индекс
, а в (28) немой индекс 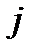 заменим буквой
заменим буквой 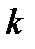 . Получаем:
. Получаем:
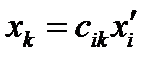 (29)
(29)
По этой формуле преобразуются координаты точки и радиус-вектора при переходе от новой системы координат к старой.
По формулам (27) и (29) преобразуются координаты радиус-вектора. Поскольку все векторы мы считаем свободными, то по этим же формулам преобразуются координаты (компоненты) любого вектора. Укажем правило для запоминания суммирования в формулах преобразования (27) и (29). Первая формула (27) выражает новые координаты через старые, суммирование производится по старым координатам, а это второй индекс у элементов матрицы 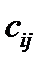 . Следовательно, суммирование производится по второму индексу. Вторая формула (29) выражает старые координаты через новые. Суммирование производится по новым координатам, а это соответствует первому индексу у элементов
. Следовательно, суммирование производится по второму индексу. Вторая формула (29) выражает старые координаты через новые. Суммирование производится по новым координатам, а это соответствует первому индексу у элементов 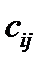 . Следовательно, суммирование идет по первому индексу.
. Следовательно, суммирование идет по первому индексу.
Символ Кронекера.
Перепишем формулы (27) и (29):
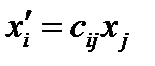 ,
, 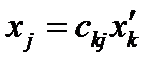 (30)
(30)
и подставим вторую в первую:
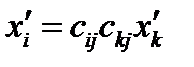 (31)
(31)
Распишем это подробно. Здесь двойное суммирование: по индексу 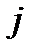 и по индексу
и по индексу 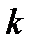 :
:
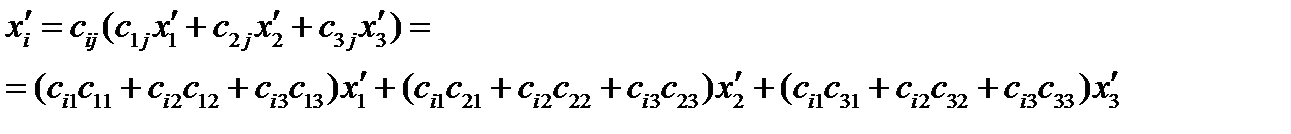 Отсюда:
Отсюда:
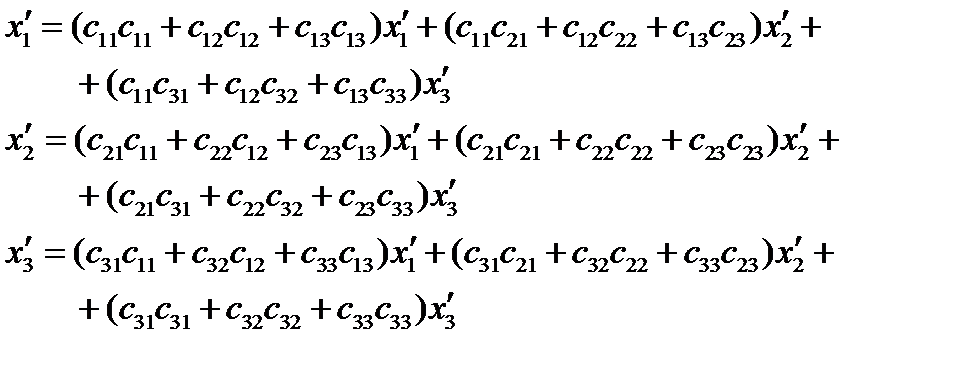
Следовательно:
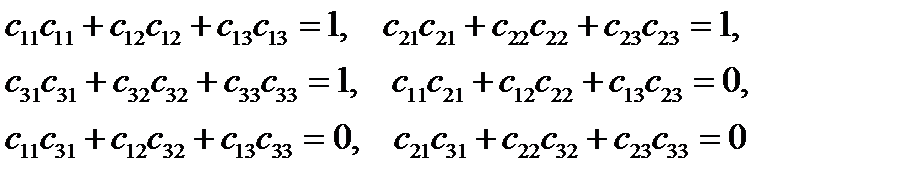 (32)
(32)
Первые три формулы можно сокращенно записать так:
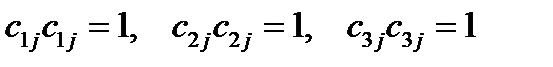 .
.
Следующие три формулы перепишем:
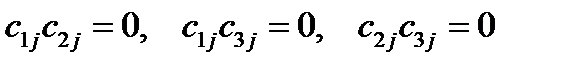
Объединяя эти две группы формул, можно записать:
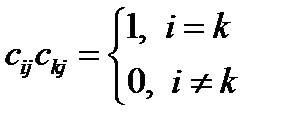 (33)
(33)
Введем так называемый символ Кронекера:
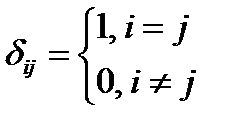 (34)
(34)
С его помощью формулу (33) запишем в виде:
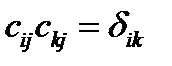 (35)
(35)
Вернемся к формулам (30) и подставим теперь первую во вторую:
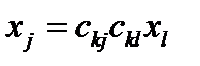
Если это выражение расписать подробно, как (32), то в итоге получим:
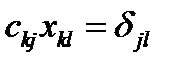 (36)
(36)
Формулы (35) и (36) есть не что иное, как выражение свойств б) и в) ортогональной матрицы преобразования системы координат, сформулированные в §3.
Переставим местами в формуле (35) индексы 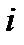 и
и 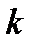 :
:
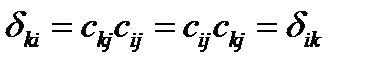 , (37)
, (37)
или 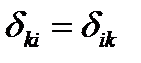 (38)
(38)
т.е. символ Кронекера симметричен.
Символ Кронекера обладает замечательным, так называемым фильтрующимсвойством, на котором и основано широкое применение этого символа. Рассмотрим выражение: 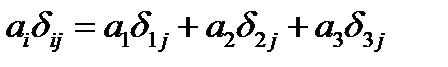 . Если
. Если 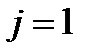 , то правая часть будет равна
, то правая часть будет равна 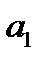 , если
, если 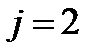 , то
, то 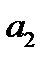 , если
, если 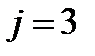 , то
, то 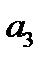 , т.е.:
, т.е.:
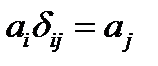 . (39)
. (39)
Это соотношение означает, что из всех компонент вектора 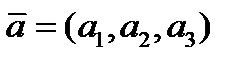 символ Кронекера «отфильтровывает» одну, а именно
символ Кронекера «отфильтровывает» одну, а именно 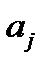 .
.
