Преобразование систем координат
Мы будем рассматривать только трехмерное евклидово пространство и только прямоугольные декартовы системы координат в нем. Как известно из курса линейной алгебры, такая система координат определяется ортонормированным единичным базисом из векторов 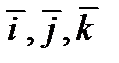 . Для удобства и для единообразия обозначений будем в дальнейшем обозначать базисные векторы через
. Для удобства и для единообразия обозначений будем в дальнейшем обозначать базисные векторы через 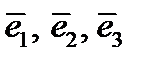 , а оси прямоугольной системы координат через
, а оси прямоугольной системы координат через 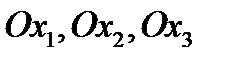 . Преобразование системы координат может включать в себя перенос начала координат без изменения направления осей (трансляция), изменение ориентации осей без переноса начала, а также и то, и другое вместе. Первый тип преобразования – трансляция, не представляет интереса, поскольку в этом случае координаты всех точек пространства изменяются на одну и ту же величину. Поэтому будем рассматривать только второй тип преобразования, считая начало координат неизменным. Изменение ориентации осей координат может происходить либо в результате вращения вокруг какой-либо оси, либо при отражении (инверсии) в какой-то плоскости.
. Преобразование системы координат может включать в себя перенос начала координат без изменения направления осей (трансляция), изменение ориентации осей без переноса начала, а также и то, и другое вместе. Первый тип преобразования – трансляция, не представляет интереса, поскольку в этом случае координаты всех точек пространства изменяются на одну и ту же величину. Поэтому будем рассматривать только второй тип преобразования, считая начало координат неизменным. Изменение ориентации осей координат может происходить либо в результате вращения вокруг какой-либо оси, либо при отражении (инверсии) в какой-то плоскости.
Рассмотрим две системы координат 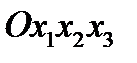 и
и 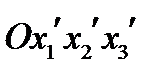 с общим началом. Первую систему координат назовем старой, а вторую новой. Разложим базисные векторы новой системы
с общим началом. Первую систему координат назовем старой, а вторую новой. Разложим базисные векторы новой системы 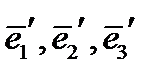 по старому базису
по старому базису 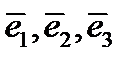 :
:
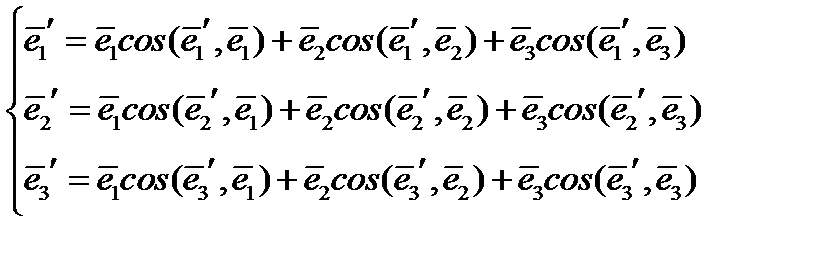 (14)
(14)
Поскольку все базисные векторы единичны, координатами (или компонентами) новых базисных векторов являются направляющие косинусы. Из направляющих косинусов составим матрицу: 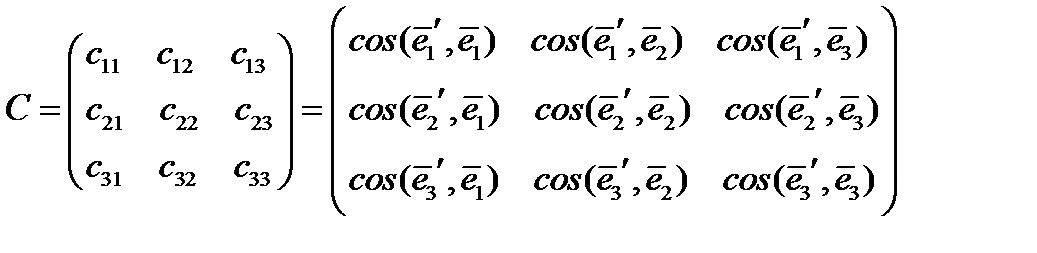 (15)
(15)
Матрица 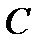 называется матрицей преобразований, ее элементы
называется матрицей преобразований, ее элементы 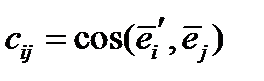 суть направляющие косинусы векторов нового базиса относительно старого базиса. Первый индекс
суть направляющие косинусы векторов нового базиса относительно старого базиса. Первый индекс 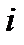 относится к новой системе, второй индекс
относится к новой системе, второй индекс 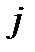 – к старой системе, так что первая строка матрицы преобразования – это направляющие косинусы базисного вектора
– к старой системе, так что первая строка матрицы преобразования – это направляющие косинусы базисного вектора 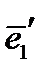 , вторая строка – направляющие косинусы вектора
, вторая строка – направляющие косинусы вектора 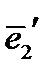 и третья – направляющие косинусы вектора
и третья – направляющие косинусы вектора 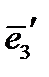 .
.
Можно поступить наоборот, разложить старые базисные векторы 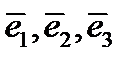 по новому базису
по новому базису 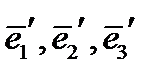 :
:
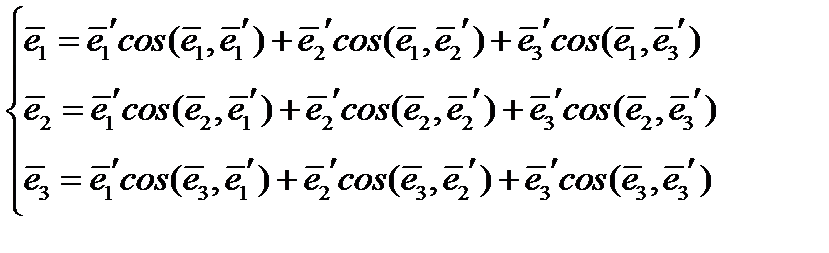 (16)
(16)
И здесь составим матрицу преобразования 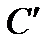 так, чтобы направляющие косинусы вектора
так, чтобы направляющие косинусы вектора 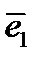 располагались в первой строке, вектора
располагались в первой строке, вектора 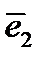 – во второй и вектора
– во второй и вектора 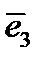 – в третьей.
– в третьей.
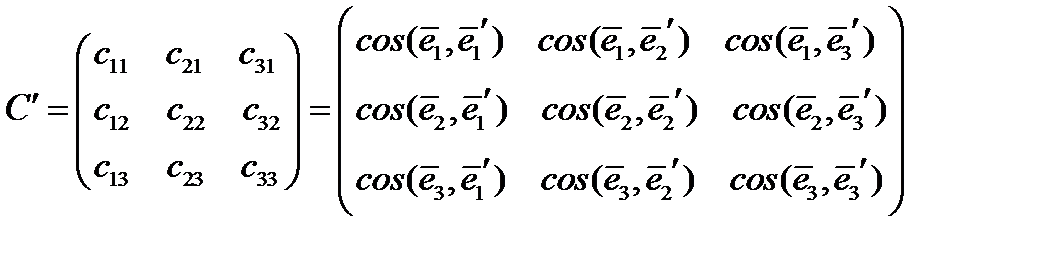 (17)
(17)
Матрица 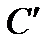 называется матрицей обратного перехода. Сравнивая матрицы переходов
называется матрицей обратного перехода. Сравнивая матрицы переходов 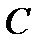 и
и 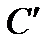 , видим, что по отношению друг к другу они транспонированы, т.е.
, видим, что по отношению друг к другу они транспонированы, т.е. 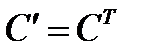 , где
, где 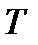 обозначает символ транспонирования.
обозначает символ транспонирования.
Рассмотрим свойства матриц преобразования на примере матрицы 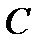 :
:
а) Матрица не симметрична, т.е. 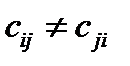 .
.
б) Сумма квадратов элементов каждого столбца и каждой строки равна единице. Это следует из того, что столбцы матрицы 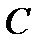 суть направляющие косинусы одного из старых базисных векторов, сумма квадратов которых, как известно, равна единице. Строки матрицы
суть направляющие косинусы одного из старых базисных векторов, сумма квадратов которых, как известно, равна единице. Строки матрицы 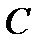 – это направляющие косинусы одного из новых базисных векторов в старом базисе и поэтому сумма их квадратов также равна единице.
– это направляющие косинусы одного из новых базисных векторов в старом базисе и поэтому сумма их квадратов также равна единице.
в) Сумма произведений элементов одного столбца (строки) на элементы другого столбца (строки) равны нулю. Это следует из ортогональности базисных векторов, как новых, так и старых, и поэтому скалярное произведение двух векторов одного базиса равно нулю.
г) Матрица перехода 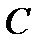 не вырождена и ее определитель равен ±1 в зависимости от того, одинакова или нет ориентация нового и старого базисов относительно друг друга. Как известно из курса векторной алгебры, тройка векторов
не вырождена и ее определитель равен ±1 в зависимости от того, одинакова или нет ориентация нового и старого базисов относительно друг друга. Как известно из курса векторной алгебры, тройка векторов 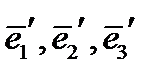 называется правой, если кратчайший поворот от вектора
называется правой, если кратчайший поворот от вектора 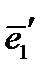 к вектору
к вектору 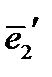 кажется происходящим в положительном направлении (против часовой стрелки, если смотреть с конца вектора
кажется происходящим в положительном направлении (против часовой стрелки, если смотреть с конца вектора 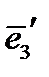 ). Составим смешанное произведение векторов нового базиса
). Составим смешанное произведение векторов нового базиса 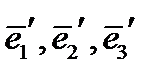 . С геометрической точки зрения оно равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если оба базиса имеют одинаковую ориентацию, например, оба правые, и со знаком минус, если ориентация базисов различна (один из них правый, другой левый). Поскольку упомянутый параллелепипед является прямоугольным и все его три размера равны единице, то и объем равен единице. С другой стороны, это же смешанное произведение
. С геометрической точки зрения оно равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если оба базиса имеют одинаковую ориентацию, например, оба правые, и со знаком минус, если ориентация базисов различна (один из них правый, другой левый). Поскольку упомянутый параллелепипед является прямоугольным и все его три размера равны единице, то и объем равен единице. С другой стороны, это же смешанное произведение 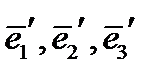 равно определителю, составленному из координат перемножаемых векторов. Поскольку при транспонировании матрицы ее определитель не изменяется, то и определитель матрицы обратного перехода тоже равен ±1.
равно определителю, составленному из координат перемножаемых векторов. Поскольку при транспонировании матрицы ее определитель не изменяется, то и определитель матрицы обратного перехода тоже равен ±1.
д) Матрицы 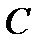 и
и 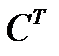 определяют два взаимнообратных преобразования базисов. Поэтому эти матрицы являются по отношению друг к другу тоже взаимно обратными. Таким образом, матрица, обратная по отношению к матрице
определяют два взаимнообратных преобразования базисов. Поэтому эти матрицы являются по отношению друг к другу тоже взаимно обратными. Таким образом, матрица, обратная по отношению к матрице 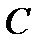 , получается простым транспонированием. Отсюда следует, что
, получается простым транспонированием. Отсюда следует, что 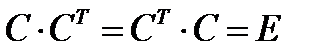 , где
, где 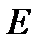 – единичная матрица. Матрица, обладающая перечисленными свойствами, называется ортогональной матрицей. Следовательно, преобразование прямоугольных систем координат осуществляется с помощью ортогональных матриц.
– единичная матрица. Матрица, обладающая перечисленными свойствами, называется ортогональной матрицей. Следовательно, преобразование прямоугольных систем координат осуществляется с помощью ортогональных матриц.
Используя теперь обозначения для элементов матрицы перехода 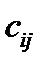 , перепишем формулы (14) и (16):
, перепишем формулы (14) и (16):
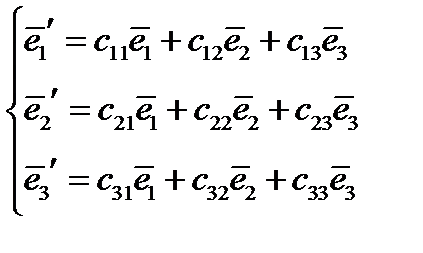 (18)
(18)
или короче: 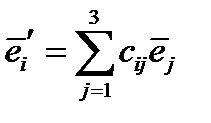 ,
, 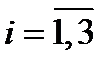 (19)
(19)
Аналогично для обратного преобразования:
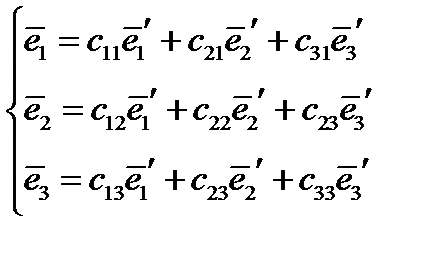 (20)
(20)
или сокращенно 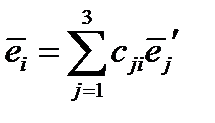 ,
, 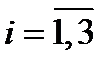 (21)
(21)
