Двухфакторный дисперсионный анализ
Данный вид анализа позволяет оценить влияние на результативный признак воздействие двух факторов как по отдельности, так и одновременно. В предыдущем разделе выяснялось, как влияет стаж работы на удовлетворенность профессии педагога. Но может влиять не только стаж, но и другие факторы. Например, пол. Для проверки данного предположения выборка была расширена, в нее были дополнительно включены 15 женщин-учителей, имеющих соответствующий стаж. Данные представлены в таблице.
| Первые 5 лет | 5 – 10 лет | 10 – 15 лет | |
| Педагоги-мужчины | |||
| Педагоги-женщины | |||
При использовании двухфакторного дисперсионного анализа выдвигаются три комплекта гипотез.
1. Но : различия показателей результативного признака, обусловленные действием гендерного фактора достоверно не превосходят случайные различия между показателями.
Н1 : различия показателей результативного признака, обусловленные действием гендерного фактора достоверно превосходят случайные различия между показателями.
2. Но : различия показателей результативного признака, обусловленные действием фактора стажа достоверно не превосходят случайные различия между показателями.
Н1 : различия показателей результативного признака, обусловленные действием фактора стажа достоверно превосходят случайные различия между показателями.
3. Но : влияние гендерного фактора, на результативный признак одинаково при разных градациях фактора стажа и наоборот.
Н1 : влияние гендерного фактора, на результативный признак различно при разных градациях фактора стажа и наоборот.
Затем необходимо действовать по следующему алгоритму. Каждому из дисперсионных разрядов приписывается буквенный символ.
| Фактор стажа | |||
| Фактор пола | A | B | C |
| D | E | F |
При этом, допустим, значение МA означает среднее арифметическое значение для результирующих показателей, находящихся в разряде А (мужчин со стажем работы до 5 лет). А МA+B+C – среднее арифметическое сразу для трех разрядов: А, В и С (всех мужчин).
Теперь необходимо определить:
1. Среднее арифметическое значение для всех показателей и общую сумму квадратов разностей всех значений и общего среднего арифметического.
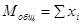
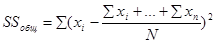
Внутригрупповые средние значения и внутригрупповые суммы квадратов разностей для каждого фактора.
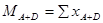
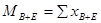
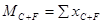
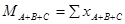
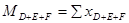
SSвг стаж =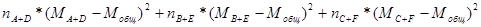 
SSвг пол =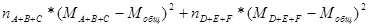 
Средние арифметические значения по всем разрядом в отдельности и межгрупповую сумму квадратов совместного влияния факторов стажа и пола.
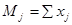
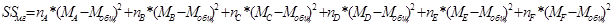Случайное рассеивание внутри групп
SSслуч = SSобщ –SSвг стаж – SSвг пол - SSмг
2. Затем следует нахождение числа степеней свободы для каждого фактора, для суммы факторов и для случайного влияния.
dfстаж = количеству дисперсионных разрядов относительно фактора стажа - 1
dfпол = количеству дисперсионных разрядов относительно фактора пола - 1
dfмг = (количество разрядов фактора стажа – 1)*(количество разрядов фактора пола – 1)
dfслуч = N – 1 - dfстаж - dfпол
3. Следующий этап – нахождение средних сумм квадратов.
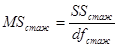
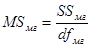
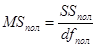
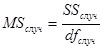
4. Нахождение эмпирических значений F-критерия и сравнение эмпирических значений с критическими.
В нашем случае это будет выглядеть следующим образом.
1. Мобщ = 7,21 SSобщ = 125,56
МA+D =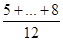 
= 5,67 MA+B+C = 
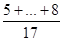= 6,88
MB+E =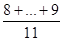 
= 8,27 MD+E+F = 
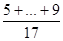= 7,53
MC+F =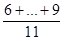 
= 7,82
SSвг стаж = 12* (5,67-7,21) 2+11*(8,27-7,21) 2+11*(7,82-7,21) 2 = 45,07
SSвг пол = 17*(6,88-7,21)2+17*(7,53-7,21)2 = 3,56
МА = (5+…+8)/6 = 5,5 МD = (5+…+8)/6 = 5,83
МВ = (8+…+7)/6 = 8,17 МЕ = (10+…+9)/5 = 8,4
МС = (6+…+8)/5 = 7 МF = (9+…+9)/5 = 8,5
SSмг=6*(5,5-7,21)2+6*(8,17-7,21)2+5*(7-7,21)2+6*(5,83-7,21)2+5*(8,4-7,21)2+6*(8,5-7,21)2=3,06
SSслуч = 125,56 - 45,07 - 3,56 - 3,06 = 73,87
2.dfстаж = 3 – 1 = 2 dfпол = 2 – 1 = 1
dfмг = (3 – 1) * (2 – 1) = 2 dfслуч = 34 – 1 – 2 – 1 – 2 = 28
3. MSстаж = 45,07 / 2 = 22,54 MSпол = 3,56 / 1 = 3,56
MSмг = 3,06 / 2 = 1,53 MSслуч = 73,87 / 28 = 2,68
4. Fстаж = 22,54 / 2,68 = 8,54 Fпол = 3,56 / 2,68 = 1,35
Fмг = 1,53 / 2,68 = 0,58
| Факторы | Fэмп | dfчисл | dfзнам | Fкр (a=0,05) | Fкр (a=0,01) | Сравнение |
| Стаж | 8,54 | 3,34 | 5,453 | Fэмп>Fкр(0,01) | ||
| Пол | 1,35 | 4,196 | 7,636 | Fэмп<Fкр | ||
| Совм. влияние стажа и пола | 0,58 | 3,34 | 5,453 | Fэмп<Fкр |
Таким образом, мы принимаем принимаем Н1 из 2-го комплекта гипотез. Нами на уровне высокой статистической значимости установлена зависимость удовлетворенности профессией учителя от стажа. В то же время не установлена зависимость удовлетворенности профессией учителя от пола. Не установлена и зависимость результирующего показателя от совместного влияния факторов стажа и пола.
Корреляционный анализ
Процедура корреляционного анализа предполагает подготовку таблицы данных (называется также матрицей наблюдения), где в первом столбце приводятся коды или фамилии испытуемых, а последующие столбцы содержат значения зарегистрированных признаков. В качестве примера можно взять Таблицу данных из Приложения.
Дальнейший этап – составление матрицы интеркорреляций. При этом исходные данные должны быть измерены в метрических шкалах. Так, результаты первых трех параметров в нашей таблице представлены в номинативной шкале и обработке не подлежат. В указанной процедуре используется формула линейной корреляции с целью вычисления сопряженности требуемых пар признаков. Например, для показателей субтестов «осведомленность» и «скрытые фигуры» значение коэффициента Rxy = 0,28. Вручную обработка матрицы занимает очень много времени, поэтому рекомендуется для этой цели использовать компьютерные программы: например, Statistica, SPSS или Excel последних версий.
В нашем случае в результате вычислений матрица принимает следующий вид:
| осведомленность | скрытые фигуры | пропущенные слова | арифметика | понятливость | исключение изображений | аналогии | числовые ряды | умозаключения | геометрическое сложение | заучивание слов | средний IQ | экстраверсия-интроверсия | нейротизм | средняя отметка | |
| Осведомленность | 0,28 | 0,37 | 0,18 | 0,15 | 0,29 | 0,25 | 0,16 | 0,01 | 0,03 | 0,45 | 0,47 | 0,14 | -0,03 | 0,40 | |
| Скрытые фигуры | 0,28 | 0,34 | 0,21 | 0,36 | 0,38 | 0,23 | 0,23 | 0,26 | 0,49 | 0,15 | 0,63 | 0,11 | 0,13 | 0,42 | |
| Пропущенные слова | 0,37 | 0,34 | 0,23 | 0,20 | 0,34 | 0,31 | 0,30 | 0,38 | 0,18 | 0,43 | 0,65 | 0,14 | -0,05 | 0,33 | |
| Арифметика | 0,18 | 0,21 | 0,23 | 0,19 | 0,17 | 0,54 | 0,51 | 0,38 | 0,39 | -0,04 | 0,57 | -0,13 | 0,06 | 0,23 | |
| Понятливость | 0,15 | 0,36 | 0,20 | 0,19 | 0,35 | 0,18 | 0,04 | 0,25 | 0,34 | 0,24 | 0,51 | -0,02 | -0,01 | 0,31 | |
| Исключение изображений | 0,29 | 0,38 | 0,34 | 0,17 | 0,35 | 0,18 | 0,25 | 0,23 | 0,19 | 0,32 | 0,57 | 0,09 | -0,02 | 0,35 | |
| Аналогии | 0,25 | 0,23 | 0,31 | 0,54 | 0,18 | 0,18 | 0,42 | 0,56 | 0,26 | 0,07 | 0,66 | -0,04 | -0,06 | 0,38 | |
| Числовые ряды | 0,16 | 0,23 | 0,30 | 0,51 | 0,04 | 0,25 | 0,42 | 0,38 | 0,28 | 0,17 | 0,61 | -0,17 | 0,29 | 0,38 | |
| Умозаключения | 0,01 | 0,26 | 0,38 | 0,38 | 0,25 | 0,23 | 0,56 | 0,38 | 0,40 | -0,01 | 0,64 | 0,02 | -0,03 | 0,22 | |
| Геометрическое сложение | 0,03 | 0,49 | 0,18 | 0,39 | 0,34 | 0,19 | 0,26 | 0,28 | 0,40 | -0,11 | 0,56 | 0,20 | 0,36 | 0,19 | |
| Заучивание слов | 0,45 | 0,15 | 0,43 | -0,04 | 0,24 | 0,32 | 0,07 | 0,17 | -0,01 | -0,11 | 0,40 | 0,15 | 0,05 | 0,34 | |
| Средний IQ | 0,47 | 0,63 | 0,65 | 0,57 | 0,51 | 0,57 | 0,66 | 0,61 | 0,64 | 0,56 | 0,40 | 0,08 | 0,11 | 0,57 | |
| Экстраверсия- -интроверсия | 0,14 | 0,11 | 0,14 | -0,13 | -0,02 | 0,09 | -0,04 | -0,17 | 0,02 | 0,20 | 0,15 | 0,08 | -0,02 | 0,09 | |
| Нейротизм | -0,03 | 0,13 | -0,05 | 0,06 |
Факторный анализ
Матрица наблюдений может содержать несколько сотен строк, в соответствии с числом наблюдаемых объектов. В этом случае корреляционный анализ, ввиду больших размеров, становится неэффективным. Возникает потребность «ужать» информацию и описать явление малым числом обобщающих факторов, которые непосредственно не наблюдаются, но характеризуют явление. Такое свертывание информации и выделение главных факторов реализуется методами факторного анализа. Методика его проведения вручную в данном пособии не приводится, так является весьма трудоемкой процедурой. Для проведения анализа рекомендуется использовать компьютерные программы, такие как Statistica, Stadia или SPSS.
Чтобы выявить главные факторы, скрытые в исходной таблице данных, вначале строится матрица интеркорреляции. Затем методами линейной алгебры исследуется внутренняя структура матрицы и определяются главные факторы, так, чтобы первый из них вносил максимальный вклад в дисперсию признаков, второй - максимальный вклад в дисперсию признаков, оставшуюся после учета главного фактора и т.д.
Таблица данных должна содержать по меньшей мере столько же строк (объектов), сколько и столбцов (зафиксированных признаков). А в идеале, чем больше объектов исследовано, тем надежнее получатся результаты.
Пример подобной матрицы данных приведен ниже.
| № | Мотивация успеха – избегания неудач | Величина IQ | Стиль учебной деятельности | Нейротизм | Самооценка | Дисциплина | Физическое здоровье | Общая успеваемость |
| n |
Факторный анализ поможет выявить причины уровня общей успеваемости в зависимости от представленных левее тестовых показателей. То есть решается следующее уравнение:
Общ.усп. =k1*МУН + k2*IQ + k3*СУД + k4*нейр-м + k5*самооценка + k6*дисц + k7*физ.зд.
При проведении анализа матрицы наблюдений, взятой из Приложения, мы получаем следующую картину.
| Фактор 1 | Фактор 2 | |
| Осведомленность | 0,011131 | 0,702881 |
| Скрытые фигуры | 0,417273 | 0,48626 |
| Пропущенные слова | 0,274693 | 0,64727 |
| Арифметика | 0,748789 | 0,057049 |
| Понятливость | 0,284776 | 0,425368 |
| Исключение изображений | 0,220683 | 0,609239 |
| Аналогии | 0,673079 | 0,235562 |
| Числовые ряды | 0,672762 | 0,17784 |
| Умозаключения | 0,711571 | 0,137342 |
| Геометрическое сложение | 0,6856 | 0,074793 |
| Заучивание слов | -0,16754 | 0,758415 |
| Средний IQ | 0,739398 | 0,665014 |
| Экстраверсия-интроверсия | -0,16457 | 0,313332 |
| Нейротизм | 0,283054 | -0,12875 |
| Средняя отметка | 0,291898 | 0,625413 |
Серьезной проблемой факторного анализа после определения вкладов главных факторов, является их интерпретация, то есть описание их физического смысла.
Мы видим, что первый фактор проявляет в себя арифметических способностях, способности к умозаключению, показателях экстраверсии (отрицательная корреляция!), пространственного мышления и общих значениях интеллекта. Второй фактор - проявляется в осведомленности и способности к заучиванию слов. Первый фактор следует интерпретировать как способность к сосредоточению и умению решать интеллектуальные задачи, второй по значимости фактор – как хорошая память и умение пользоваться усвоенной ранее информацией.
В истории психологии факторный анализ связан с решением ряда теоретических задач в области исследования интеллекта. Ф. Гальтон, сформулировавший основные идеи метода, пытался при помощи его доказать, что высокий уровень мыслительных способностей является полностью врожденным явлением. Ч. Спирмен, разработавший математическое обоснование данного метода, на основе анализа корреляций между результатами различных тестов выдвинул идею единого генерального фактора, лежащего в основе успешности выполнения любых тестов, связанных с измерением интеллектуальных свойств. А Л. Терстоун разработал концепцию мультифакторного анализа и при его помощи обосновал свою теорию интеллекта.
В настоящее время факторный анализ широко используется как для решения исследовательских задач, так и при конструировании психодиагностических методик. Факторный анализ является важнейшим инструментом для математического моделирования.
Следует отметить, что математическое моделирование – это процедура описания различных процессов (экономических, биологических, социально-психологических) посредством математического аппарата. Указанная процедура включает в себя выделение всех факторов процесса, определение доли вклада каждого из факторов, выявление закономерностей их функционирования и вероятностное предсказание протекания всего процесса в дальнейшем.
Кластерный анализ
Кластерный (таксономический) анализ используется с целью упорядочивания объектов и объединения их в однородные разряды. В результате исходная выборка объектов разделяется на группы схожих между собой объектов, называемых кластерами. Кластер – это группа объектов, характеризующихся повышенной плотностью (сгущенность внутри разряда) и дисперсией.
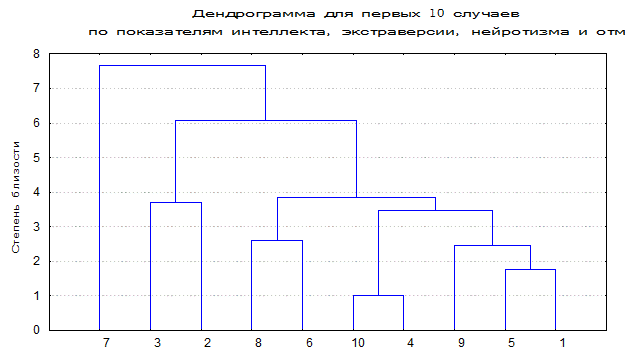
Результаты процедуры представляются графически в виде дендрограммы – древовидного графика. Алгоритм проведения данного вида анализа в настоящем пособии не рассматривается, так как, во-первых, это выходит за рамки изучаемого курса, а во-вторых, подобная задача легко может быть выполнена при помощи доступных статистических программ (в первую очередь это Statistica и SPSS).
Ниже в качестве примера приведен результат кластерного анализа показателей из Таблицы данных. Для обработки взяты первые 10 человек и рассмотрены показатели их интеллекта, экстраверсии-интроверсии, нейротизма и средней отметки. По горизонтальной шкале отложены личные номера оптантов, как они приведены в таблице. Лица принадлежащие к одному кластеру обладают наибольшей степенью близости исследуемых параметров. С начала в единый кластер объединяются 2 объекта с наиболее близкими показателями (№ 3 и 2, 8 и 6, 10 и 4, 5 и 1 ). Затем к кластеру присоединяется еще один объект с похожими параметрами (9 объединяется с кластером 5-1), потом следующий и так до конца.
[1] Сидоренко Е.В. Методы математической обработки в психологии. СПб, 1996.
[2] Наследов А.Д., Тарасов С.Г. Применение математических методов в психологии. СПб, 2001.
http://pedagogics-student.ru/index.php?action=list_category&id=330