Задачи для самостоятельного решения
Найти общее (частное) решение уравнения
Найти общий интеграл уравнения:
6.1. 
6.2. 
6.3. 
Ответы:
6.1.  ;
;
6.2.  ;
;
6.3. 
Контрольные вопросы.
1. Какое уравнение называется дифференциальным? Как определяется порядок уравнения? Запишите его общий вид Приведите примеры.
2. Какое уравнение называется дифференциальным уравнением первого порядка? Запишите его общий вид. Приведите примеры.
3. Что называется решением дифференциального уравнения первого порядка Запишите его общий вид. Приведите примеры.
4. Сформулируйте теорему существования и единственности решения дифференциального уравнения первого порядка
5. Сформулируйте задачу Коши для обыкновенного дифференциального уравнения первого порядка. Что называется общим и частным решением дифференциального уравнения первого порядка? Общим и частным интегралом?
6. Какое решение называется особым решением дифференциального уравнения?
7. Каков геометрический смысл дифференциального уравнения первого порядка, его общего и частного решения?
8. Какое уравнение называется дифференциальным уравнением с разделяющимися переменными? Приведите примеры.
9. Какая функция  называется однородной функцией
называется однородной функцией 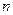 -ого порядка? Нулевого порядка? Первого порядка? И т.д. Приведите примеры.
-ого порядка? Нулевого порядка? Первого порядка? И т.д. Приведите примеры.
10. Какое дифференциальное уравнение первого порядка называется однородным? Приведите примеры.
11. Метод решения однородного уравнения.
12. Какое дифференциальное уравнение первого порядка называется линейным относительно переменной 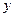 ?Относительно переменной
?Относительно переменной 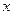 ?Приведите примеры.
?Приведите примеры.
13. Методы решения линейного дифференциального уравнения первого порядка.
14. Какое дифференциальное уравнение первого порядка называется уравнением Бернулли? Метод его решения.
15. Какое уравнение называется дифференциальным уравнением в полных дифференциалах? Приведите примеры. Метод решения.
Дифференциальные уравнения первого порядка. Справочная таблица №1
| Тип уравнения | Вид уравнения | Признаки уравнения | Указания к решению |
| 1. Уравнение с разделяющимися переменными | а)  б) б)   | а)  б) б)   | а)   б) б)    |
| 2. Однородное уравнение | а)  б) б)   | а)   б) б)   | а) Подстановкой y=ux,  уравнение сводится к уравнению с разделяющимися переменными. б) уравнение удобно предварительно записать в виде уравнение сводится к уравнению с разделяющимися переменными. б) уравнение удобно предварительно записать в виде  |
| 3.Линейное уравнение |  |   | 1. Метод вариации произвольной постоянной 2. Метод Бернулли  , ,  |
| 4. Уравнение Бернулли |  |   ; ;  | Решается тем же методом, что и тип 3. |
| 5.Уравнение в полных дифференциалах. |   |  |  или или   -область определения функций -область определения функций  и и  |
Замечание. Если удобно рассматривать уравнение не в виде  , а в виде
, а в виде  , где
, где  , то всюду в указаниях надо поменять местами x и y
, то всюду в указаниях надо поменять местами x и y
