Функции нескольких переменных

§ 1 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

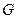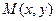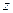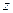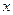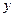Определение 1. Пусть - некоторая область в плоскости . Если каждой точке этой области по опреде-лённому правилу соответствует вполне определённое значение величины , то говорят, что - это функция двух независи -мых переменных (или аргументов) и , определённая в области 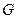. Символически это обозначается таким образом:

и т.д.

Как и функция одной переменной, функция двух перемен -ных существует не для всех значений своих аргументов.

Определение 2. Совокупность пар , при которых вы - ражение имеет смысл, называется областью опреде -ления или областью существования функции .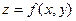

Замечание.Аналогичным образом можно ввести понятие функции 3 – х и более переменных.

Например, если каждой точке 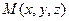трёхмерного про- странства по некоторому правилу ставится в соответствие не -которое действительное число 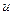, то говорят, что в простран- стве задана функция трёх переменных и т.д.

ПРИМЕРЫ.

Найти области определения следующих функций:

Эта функция определена для множества точек плоскости, удовлетворяющих условиям:

.

Это кольцо, ограниченное окружностями радиусов 1 и 2, причём граничные окружности не входит в область опре -деления.

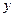
0 1 2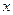

. Область определения этой функции определяется условиями:

Отсюда получаем эквивалентные условия:

Третье условие, явно, является излишним. Получаем полосу:

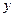
0 1 2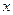

Геометрическим изображением функции двух переменных является поверхность в трёхмерном пространстве, опреде -ляемая уравнением .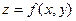

§ 2. ПРЕДЕЛ И НЕПРЕПЫВНОСТЬ ФУНКЦИИ 2 - Х

ПЕРЕМЕННЫХ.

Определение 1. 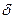- окрестностью точки 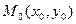называется множество точек плоскости, удовлетворяющих условию:

Определение 2. Последовательность точек называется сходящейся к точке 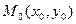,если для любого существует номер , начиная с которого (т.е. для всех ) все точки содержатся в 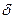- окрест -ности этой точки.

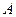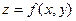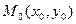Определение 3. Число называется пределом функции при , если для любой после- довательности точек , сходящейся к точке , последовательность значений функции в этих точ- ках . Или, другими словами, число 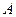назы- вается пределом функции 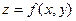при , если для любого существует , такое что для всех точек 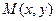, попадающих в 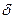- окрестность точки 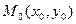, выполняется неравенство : , или .

Это обозначается таким образом:

Определение 4. Функция 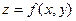называется непре -рывной в точке 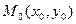, если

Определение 5. Функция непрерывная в каждой точке некоторой области, называется непрерывной в этой области.

Например, функция непрерывна в каждой точке плоскости 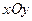; функция непрерывна везде, кроме точки .

§ 3. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ 2 – Х

ПЕРЕМЕННЫХ. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ.

1. Частные производные функции 2-х переменных

Пусть функция 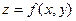определена в некоторой области плоскости 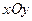. Пусть, далее точки

.

Полным приращением данной функции в точке называется разность:

. (1)

Если при вычислении приращения меняем только одну переменную, другую оставляя без изменения, то получим соответствующие частные приращения:

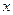, (приращение по ), (2)

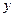, (приращение по ), (3)

Если равенство (2) разделить на и перейти к пределу при , то получим частную производную функции 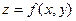по переменной 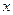, которая обозначается следую-щим образом:

. (4)

Аналогичным образом вводится частная производная функции 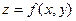по переменной :

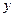(5)

ПРИМЕРЫ: Найти частные производные следующих функций.

1. . Тогда

2.

Найдём частные производные

3.

При вычислении частных производных следует помнить следующие правила: