Метод итерации для решения систем уравнений
Схема метода Гаусса, дающая точное решение, при большом числе неизвестных cтановится сложной. В этом случае иногда пользуются приближенными численными методами. Один из них – метод итерации.
Пусть дана линейная система
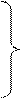
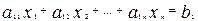
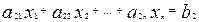
------------------------------------- (16.29)
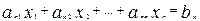
Введем в рассмотрение матрицы
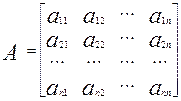 ,
, 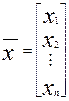 ,
, 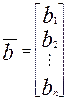 .
.
Тогда систему (16.29) коротко можно записать в виде матричного уравнения
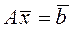 (16.30)
(16.30)
Предполагая, что диагональные коэффициенты
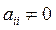 ,
, 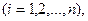
разрешим первое уравнение системы (16.29) относительно х1, второе-относительно х2, и т.д. Тогда получим эквивалентную систему.
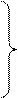
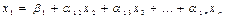
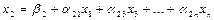
------------------------------------------------ . (16.31)
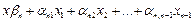
Для лучшего запоминания она может быть переписана в виде:
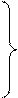
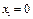 ×
× 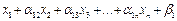
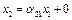 ×
× 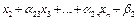
------------------------------------------------------ (16.31')
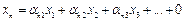 ×
× 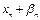
Здесь 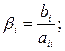
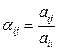 при
при 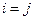
и 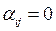 при
при 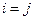
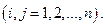
Введем матрицы
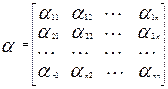 и
и 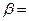
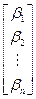 .
.
Тогда система (16.31') может быть записана в матричной форме
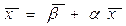 . (16.32)
. (16.32)
Будем решать систему (16.31' ) методом последовательных приближений.
За нулевое приближение примем, например, столбец свободных членов
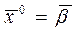 .
.
Далее начинаем строить приближения.
Первое приближение:
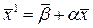 .
.
Второе приближение:
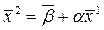 и.т.д.
и.т.д.
Обобщая, можно сказать, что (k+1)-e приближение вычисляют по формуле
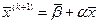 (k) (k=0,1,2,…) (16.33)
(k) (k=0,1,2,…) (16.33)
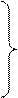 Если последовательность приближений
Если последовательность приближений 
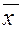 (0),
(0), 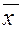 (1),…,
(1),…, 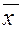 (k)…
(k)… 
имеет предел 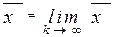 (k),
(k),
то этот предел является решением системы (16.31).
Действительно переходя к пределу в равенстве (16.33):
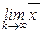 (k+1)
(k+1) 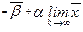 (k) или
(k) или
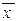
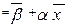 ,
,
т.е. предельный вектор 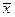 является решением системы (16.32), а, следовательно, и системы (16.29).
является решением системы (16.32), а, следовательно, и системы (16.29).
Напишем формулу приближений в развернутом виде:
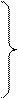
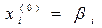
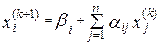 (16.33')
(16.33')
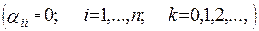
Пример.Решить систему методом итерации
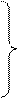 |
4х1+0,24х2-0,08х3=8
0,09х1+3х2-0,15х3=9 (16.34)
0,04х1-0,08х2+4х3=20
Обращаем внимание на тот факт, что здесь диагональные коэффициенты 4; 3; 4 системы значительно преобладают над остальными коэффициентами при неизвестных (это есть условие сходимости процесса итерации).
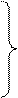 Приведем систему к нормальному виду:
Приведем систему к нормальному виду:
х1=2-0,06х2+0,02х3
х2=3-0,03х1+0,05х3 (16.35)
х3=5-0,01х1+0,02х2
Система (16.35) в матричной форме может быть записана так:
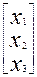 =
= 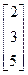 +
+ 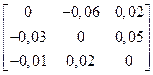 ·
· 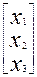 .
.
За нулевые приближения корней системы (16.34) можно принять
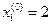 ;
; 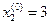 ;
; 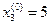 .
.
Подставляя эти значения в правые части уравнений (16.35), получаем первые приближения корней:
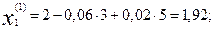
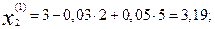
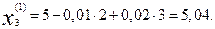
Далее, подставляя эти найденные приближения в формулу (16.35), получаем вторые приближения корней:
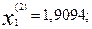
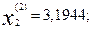
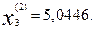
После следующей подстановки получатся третьи приближения корней.
Сведем результаты вычислений в таблицу:
| k | 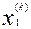 | 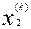 | 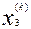 |
| 1,92 1,9094 1,90923 | 3,19 3,1944 3,19495 | 5,04 5,0446 5,04485 |
Замечание. Можно доказать, что сходимость процесса итерации зависит только от свойств матрицы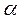 . Окончательные значения корней xi не зависят от выбора нулевых приближений
. Окончательные значения корней xi не зависят от выбора нулевых приближений 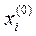 . Поэтому начальный вектор
. Поэтому начальный вектор 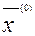 в процессе итерации может быть взят произвольным. За компоненты начального вектора целесообразно выбрать приближенные значения корней системы, находимые грубой прикидкой.
в процессе итерации может быть взят произвольным. За компоненты начального вектора целесообразно выбрать приближенные значения корней системы, находимые грубой прикидкой.
Условия сходимости процесса итерации формулируются следующей
теоремой:
Если для приведенной системы (16.31) выполнено, по меньшей мере, одно из условий
1) 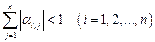
или
2) 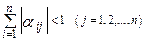
то, процесс итерации(16.33) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Следствие. Для системы
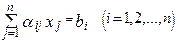
метод итерации сходится, если выполнены неравенства
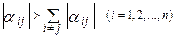 ,
,
т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
Теорема сходимости накладывает жесткие условия на коэффициенты решаемой системы. Однако, если определитель матрицы системы не равен нулю, то с помощью линейного комбинирования уравнений исходной системы последнюю можно заменить равносильной системой, в которой условия сходимости выполняются.
Поступают следующим образом. Из заданной системы выделяют уравнения с такими коэффициентами, модуль одного из которых больше суммы модулей всех остальных коэффициентов уравнения. Каждое выделенное уравнение выписывают в такую строку новой системы, чтобы наибольший по модулю коэффициент оказался диагональным.
Из оставшихся неиспользованных уравнений системы составляют линейно независимые между собой линейные комбинации с таким расчетом, чтобы был соблюден указанный выше принцип комплектования новой системы, и все свободные строки оказались заполненными. При этом необходимо, чтобы каждое неиспользованное ранее уравнение попало хотя бы в одну линейную комбинацию, являющуюся уравнением новой системы.
Пример: Систему привести к виду, годному для применения метода итерации.
 (А) 2х1+3х2-4х3+х4-3=0
(А) 2х1+3х2-4х3+х4-3=0
(Б) х1-2х2-5х3+х4-2=0
(В) 5х1-3х2+х3-4х4-1=0
(Г) 10х1+2х2-х3+2х4+4=0
Решение. В уравнении (Б) коэффициент при x3по модулю больше суммы модулей остальных коэффициентов, поэтому можно принять это уравнение за третье уравнение новой системы. Коэффициент при x1 в уравнении (Г) также больше суммы модулей остальных коэффициентов уравнения (Г), поэтому это уравнение можно принять за первоеуравнение новой системы. Таким образом, новая система имеет следующий вид:
(I) 10х1+2х2-х3+2х4+4=0
(II) ---------------------------
(Ш) х1-2х2-5х3+х4-2=0
(IV) ---------------------------
Легко заметить, что для получения уравнения (II) с максимальным по модулю коэффициентом при х2 достаточно составить разность (А) - (Б):
(II) х1+5х2+х3+0х4-1=0.
Теперь в новую систему вошли уравнения (А), (Б) и (Г).
Поэтому в уравнение (IV) обязательно должно войти уравнение (В) исходной системы. После нескольких попыток можно найти какую-либо комбинацию.
В частности, за уравнение (IV) можно взять линейную комбинацию
2(А) – (Б) + 2(В) – Г, т.е.
(IV) 3x1 +0x2 +0x3 – 9x4 -10 = 0.
В итоге получаем преобразованную систему уравнений I – IV, эквивалентную исходной и удовлетворяющую условиям сходимости. Разрешив эту систему относительно диагональных неизвестных, будем иметь систему , к которой можно применить метод итераций:
 х1=0х1-0,2х2+0,1х3-0,2х4-0,4
х1=0х1-0,2х2+0,1х3-0,2х4-0,4
х2=0,2х1+0·х2-0,2х3+0·х4+0,2
х3=0,2х1-0,4х2+0х3+0,2х4-0,4
х4=0,333х1+0х2+0х3+0·х4-1,111
