Решение типового примера. На рынке обращается 6 ценных бумаг ЦБ-1 – ЦБ-6

Задание 3

На рынке обращается 6 ценных бумаг ЦБ-1 – ЦБ-6. Известна доходность (в %) этих ценных бумаг за последние 5 периодов:

Период	ЦБ-1	ЦБ-2	ЦБ-3	ЦБ-4	ЦБ-5	ЦБ-6
	16,07	15,30	16,04	15,38	15,32	15,84
	15,73	15,00	16,11	15,13	14,95	15,17
	15,58	14,64	16,02	14,66	15,21	15,55
	16,13	14,26	15,31	15,47	14,72	15,37
	15,42	14,75	15,56	15,14	14,64	15,17

Необходимо:

1. Определить ковариации между доходностями каждой пары ценных бумаг.

2. Определить доходность и риск портфеля.

3. Найти с помощью надстройки «Поиск решения» в Microsoft Excel минимальный риск портфеля.

4. Найти с помощью надстройки «Поиск решения» в Microsoft Excel риск, получаемый при максимальной доходности портфеля.

5. Построить эффективное множество портфелей ценных бумаг по модели Марковица и выбрать на нем портфель с приемлемым соотношением доходности и риска.

6. Построить в Microsoft Excel график зависимости риска портфеля от максимального значения дохода, достигаемого при этом риске.

7. Выбрать портфели для инвесторов консервативного, умеренно-агрессивного и агрессивного типов, обосновав свой выбор.

Решение.

1. Определим ковариации между доходностями каждой пары ценных бумаг.

Для этого создаем в Microsoft Excel новую книгу и сохраняем ее под названием «Портфель ценных бумаг». На листе 1 новой книги в ячейки А1:G7 вводим исходные данные задачи, как на рис. 24.

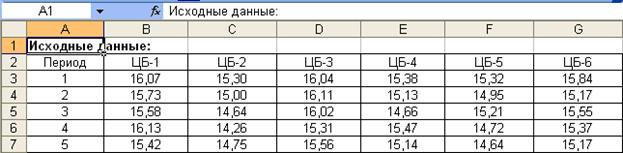
Рис. 23. Ввод исходных данных задачи 3

Далее в ячейках А11:G17 формируем таблицу для расчета ковариационной матрицы, в ячейки В12:В17 вводим формулы с использованием встроенной функции «КОВАР» (категория «Статистические»), в качестве параметров которой указываются диапазоны ячеек с доходностями соответствующих ценных бумаг за все периоды (рис. 25).

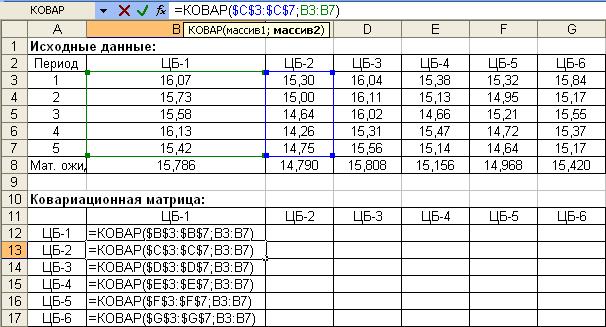
Рис. 24. Ввод формул для определения ковариации

Затем скопируем формулы в ячейках В12:В17 в остальные ячейки данной таблицы, в результате получим следующее:

Рис. 25. Ковариационная матрица (результат вычисления)

Итак, получили ковариационную матрицу, элементами которой являются ковариации между доходностями каждой пары ценных бумаг.

2. Определим доходность и риск портфеля

Сначала найдем математическое ожидание доходности каждой ценной бумаги. Математическое ожидание доходности вычисляется как среднее значение доходности, полученной во всех периодах. Определим математические ожидания каждой ценной бумаги в ячейках В8:G8 с помощью встроенной функции «СРЗНАЧ» Microsoft Excel (рис. 26).

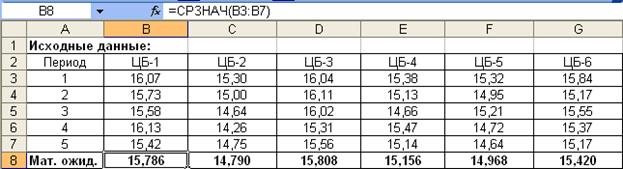
Рис. 26. Определение математических ожиданий

Для определения доходности и риска портфеля добавим к ковариационной матрице напротив обозначения каждой ценной бумаги столбец с долей этой ценной бумаги в портфеле (в ячейки Н12:Н17) вводим нулевые первоначальные значения), ниже которого вводим формулу суммы долей (рис. 27). Для удобства нахождения риска портфеля продублируем с помощью равенства столбец долей ценных бумаг в строку (ячейки В18:G18).

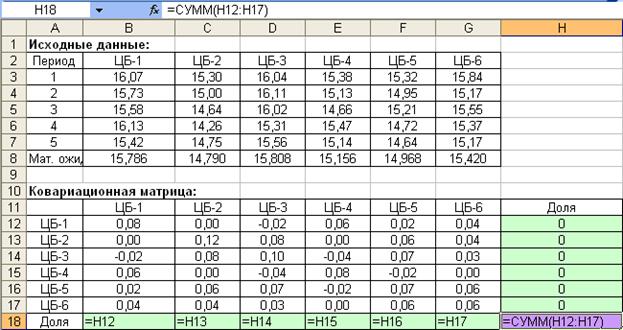
Рис. 27. Ввод формулы для определения суммы долей ценных бумаг в портфеле

Для нахождения риска портфеля по формуле (12) сначала составим таблицу со значениями ( 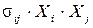) для всех 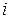и 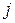: в ячейку В22 вводим формулу: «=$H12*B$18*B12», затем копируем ее во все остальные ячейки таблицы нахождения риска портфеля (рис. 28).

Все значения полученной таблицы будут равны нулю, поскольку доля ценных бумаг в портфеле не задана.

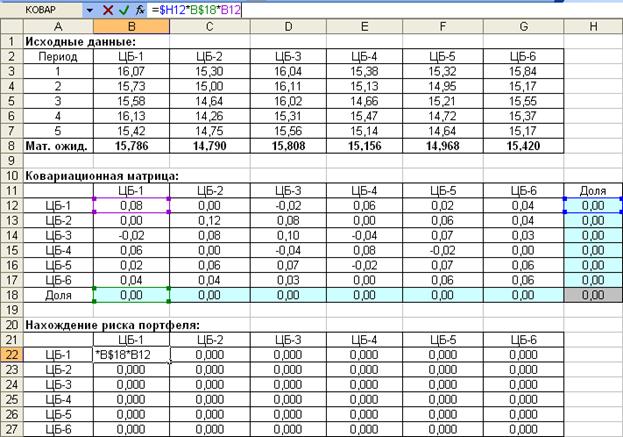
Рис. 28. Нахождение риска портфеля (промежуточные расчеты)

Для окончательного расчета риска портфеля по формуле (12) в отдельную ячейку В29 вводим формулу суммы всех значений таблицы нахождения риска портфеля: «=СУММ(B22:G27)».

Ниже, в ячейку В30, вводим формулу (11) расчета ожидаемой доходности портфеля: «=СУММПРОИЗВ(B8:G8;B18:G18)».

В результате в ячейках В29 и В30 получим значения риска и доходности портфеля соответственно (рис. 29).

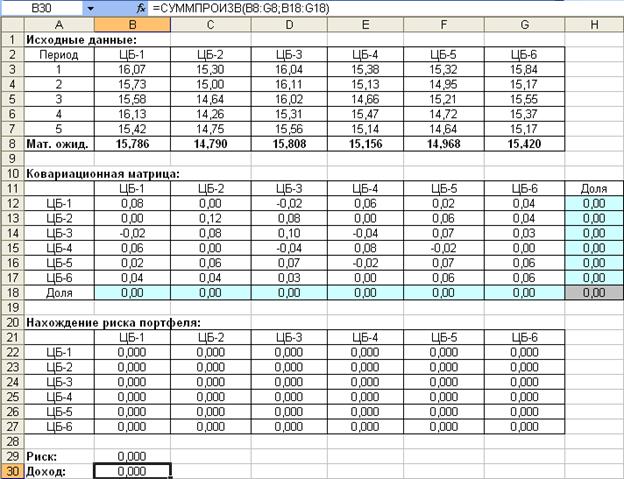
Рис. 29. Вычисление риска и доходности портфеля

Значения риска и доходности портфеля в ячейках В29 и В30 будут равны нулю до тех пор, пока не будут заданы доли ценных бумаг в портфеле, после чего пересчет произойдет автоматически (рис. 29).

3. Найдем с помощью надстройки «Поиск решения» в Microsoft Excel минимальный риск портфеля ценных бумаг, т.е. найдем такую структуру портфеля (доли ценных бумаг), чтобы риск портфеля принимал минимальное значение при соблюдении определенных условий.

Для этого необходимо выделить ячейку, содержащую значение риска портфеля (ячейку В29), и выполнить команду «Сервис»/ «Поиск решения…»[1]. В открывшемся окне надстройки «Поиск решения…» в поле «Целевая ячейка» уже будет указано: «$B$29» (т.е. ячейка, содержащая значение риска портфеля), необходимо установить флажок «Равной минимальному значению», в поле «Изменяя ячейки» – выбрать «$H$12:$H$17», т.е. ячейки со значениями доли каждой ценной бумаги в портфеле (рис. 30). Далее указываем ограничения следующим образом: нажимаем кнопку «Добавить», и в открывшемся окне вводим ограничение неотрицательности доли ценных бумаг в портфеле (рис. 31), еще раз нажимаем кнопку «Добавить» и вводим ограничение на сумму долей ценных бумаг, которое должно быть равно 1 (рис. 32), нажимаем «ОК». В окне поиска решений (рис. 30) нажимаем «Выполнить».

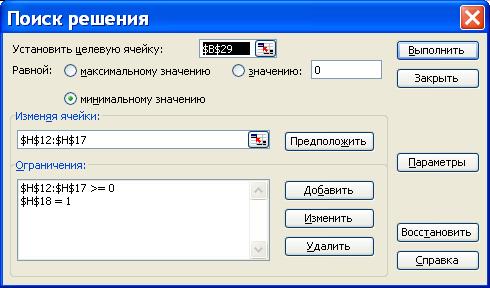
Рис. 30. Окно "Поиск решений"

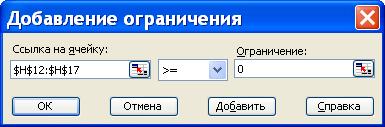
Рис. 31. Ввод первого ограничения

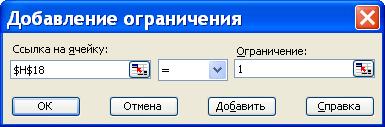
Рис. 32. Ввод второго ограничения

В результате получим минимальный риск портфеля, равный 0,022 – ячейка В29, а также долю каждой ценной бумаги в портфеле – ячейки Н12:Н17 (рис. 33).

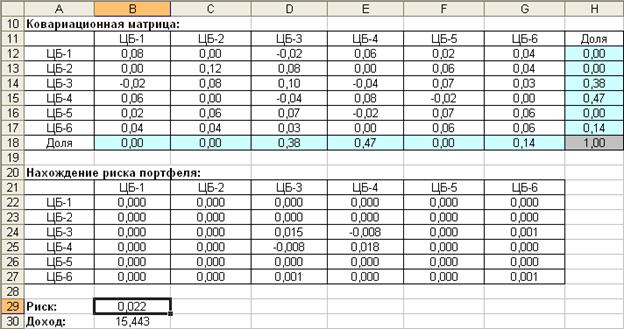
Рис. 33. Минимальный риск портфеля

4. Аналогично с помощью надстройки «Поиск решения» в Microsoft Excel найдем риск, получаемый при максимальной доходности портфеля, т.е. найдем такую структуру портфеля (доли ценных бумаг), чтобы доходность портфеля принимала максимальное значение при соблюдении определенных условий.

Для этого необходимо выделить ячейку, содержащую значение доходности портфеля (ячейку В30), и выполнить команду «Сервис»/ «Поиск решения…». В открывшемся окне надстройки «Поиск решения…» в поле «Целевая ячейка» уже будет указано: «$B$30», необходимо установить флажок «Равной максимальному значению», в поле «Изменяя ячейки» – выбрать «$H$12:$H$17», далее указываем все ограничения (рис. 34).

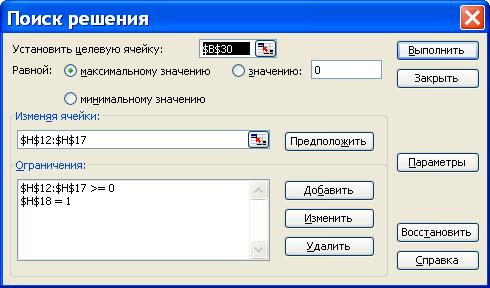
Рис. 34. Окно «Поиск решения»

В результате риск портфеля, соответствующий его максимальной доходности в 15,808% (ячейка В30), составит 0,100 (ячейка В29), доли ценных бумаг в портфеле представлены в ячейках Н12:Н17 (рис. 35).

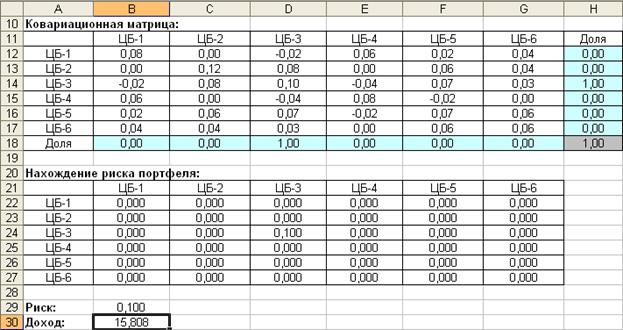
Рис. 35. Максимальная доходность портфеля

5. Построим эффективное множество портфелей ценных бумаг по модели Марковица и выберем на нем портфель с приемлемым соотношением доходности и риска.

Эффективное множество портфелей можно построить с помощью надстройки «Поиск решения» в Microsoft Excel, т.е. при заданном значении риска портфеля (стандартного отклонения портфеля), рассчитанного по формуле (12), необходимо максимизировать величину дохода, полученного при помощи формулы (11).

Диапазон, в котором лежат значения риска портфелей, составляющих эффективное множество, имеет нижнюю границу, равную минимальному риску портфеля ценных бумаг, и верхнюю границу, равную риску при максимальной доходности портфеля.

Теперь определим максимальную доходность портфеля и его структуру (т.е. доли в нем ценных бумаг), зафиксировав значение риска в этом диапазоне с некоторым шагом, например 0,01 (последним значением риска возьмем не 0,102, т.к. это значение выходит за допустимый диапазон риска, а верхнюю границу диапазона – 0,100).

Для поиска решения при риске 0,022 добавим новое ограничение «$B$29=0,022». Тогда окно поиска решений будет выглядеть следующим образом (рис. 36)[2]:

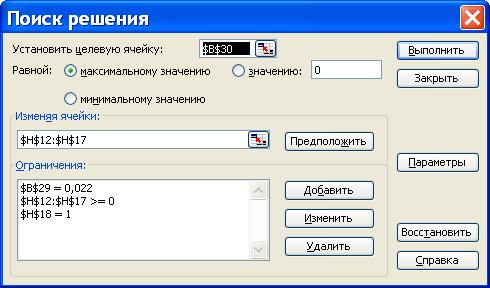
Рис. 36. Расчет максимальной доходности при риске 0,022

В результате для риска 0,022 получим следующие результаты: доходность составляет 15,457%, доля ЦБ-1=0, доля ЦБ-2=0, доля ЦБ-3=0,41, доля ЦБ-4=0,46, доля ЦБ-5=0, доля ЦБ-6=0,13.

Поскольку при новом поиске решения полученные результаты изменятся на новые, то создадим таблицу, в которую будем вводить все результаты вычислений при различных значениях риска. Запишем полученные при риске 0,022 результаты в отдельные ячейки B33:I33 (рис. 37).

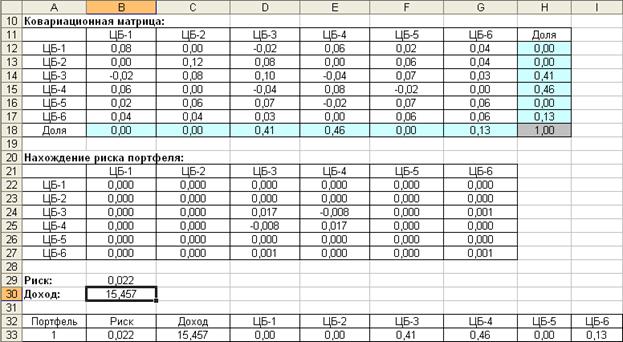
Рис. 37. Результат вычисления при риске 0,022

Теперь определим максимальную доходность портфеля и его структуру, зафиксировав значение риска на следующем шаге (0,022+0,01). Для этого изменим первое ограничение на «$B$29=0,032». Получим следующие результаты, которые перенесем в ячейки B34:I34, и т.д.

Определив показатели для всех значений риска в диапазоне от минимального до максимального с некоторым шагом (в данном примере 0,01) и сохранив результаты в отдельных ячейках (в т.ч. и значения долей ценных бумаг в портфеле, при которых получается данное значение риска), получим эффективное множество портфелей ценных бумаг, в которое входят портфели, обеспечивающие максимальную ожидаемую доходность для диапазона уровня риска от 0,022 до 0,100. Эффективное множество портфелей ценных бумаг представлено в ячейках А32:I41 (рис. 38).

Выбрать на нем портфель с приемлемым соотношением доходности и риска

6. Построим в Microsoft Excel график зависимости риска портфеля от максимального значения дохода, достигаемого при этом риске.

Для этого выделяем значения столбцов «Риск» и «Доход» эффективного множества портфелей ценных бумаг, затем выполняем команду «Вставка»/ «Диаграмма», в открывшемся окне выбираем тип «Точечная». Пройдя все шаги построения диаграммы и указав все ее параметры, получает следующий график зависимости риска портфеля от максимального значения дохода, достигаемого при этом риске (рис. 38):

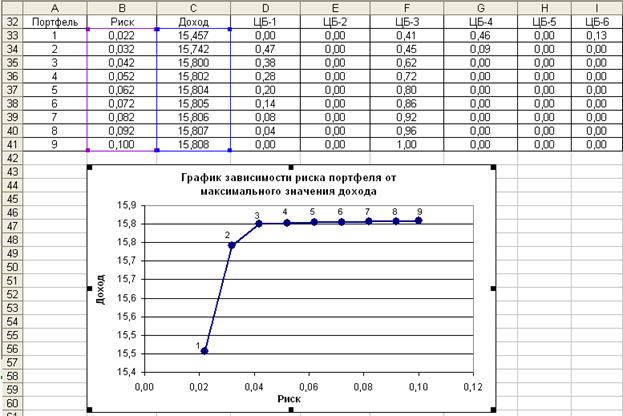
Рис. 38. Эффективное множество портфелей ценных бумаг

7. Выберем портфели для инвесторов консервативного, умеренно-агрессивного и агрессивного типов.

Конечный выбор портфеля инвестором зависит от его стратегии поведения на рынке. Консервативный инвестор выберет 1-й портфель (вложит 41% средств в ЦБ-3, 46% в ЦБ-4 и 13% в ЦБ-6), при этом инвестор получит минимальную доходность при минимуме риска.

Если инвестор намерен вести политику агрессивного роста стоимости портфеля, то он выберет 3-й или 4-й портфель, т.к. они обеспечивают высокую доходность, правда при достаточно большом риске нестабильности получения дохода. Выбор инвестором 5-9-го портфелей маловероятен, т.к. они дают практически такую же доходность, как и 3-й или 4-й портфель, но при заметном увеличении риска.

Умеренно-агрессивный инвестор, скорее всего, выберет 2-й портфель, поскольку он готов пойти на рискованные вложения, но в ограниченном объеме, подстраховывая себя вложениями в слабодоходные, но и малорискованные ценные бумаги.

[1] Если во вкладке «Сервис» отсутствует пункт «Поиск решения…», необходимо выполнить команду «Сервис»/ «Надстройки…», и в открывшемся окне выбрать надстройку «Поиск решения», после чего во вкладке «Сервис» появится выбранный пункт.

[2] Если поиску решения не удается найти решение, то в окне поиска решения нужно нажать кнопку «Параметры» и установите большее значение предельного числа итераций (например, 1000) и/или меньшее значение относительной погрешности (например, 0,001).