Линейные дифференциальные уравнения. Передаточные функции
При описании автоматических систем управления широко используют символическую форму записи линейных дифференциальных уравнений. Рассмотрим уравнение системы, изображенной на рис 2.1:
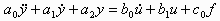 (2.6)
(2.6)
Введем для операции дифференцирования обозначение 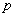 , т. е.
, т. е.
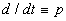 ,
, 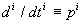 .
.
Используя его, уравнение (2.6) можно записать в виде
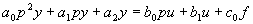 (2.7)
(2.7)
При записи и преобразовании дифференциальных уравнений оператор (операцию дифференцирования) 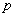 можно рассматривать как алгебраический сомножитель, а, выражение
можно рассматривать как алгебраический сомножитель, а, выражение 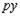 — как произведение, не обладающее свойством коммутативности: нельзя вместо
— как произведение, не обладающее свойством коммутативности: нельзя вместо 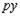 писать
писать 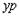 . Учитывая это замечание, перепишем (2.7), вынеся
. Учитывая это замечание, перепишем (2.7), вынеся 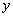 и
и 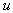 за скобки:
за скобки:
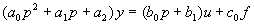 (2.8)
(2.8)
Введем обозначения 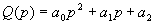 ,
, 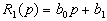 ,
, 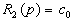 . C помощью этих обозначений уравнение (2.8) можно записать в более компактной форме
. C помощью этих обозначений уравнение (2.8) можно записать в более компактной форме
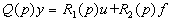 . (2.9)
. (2.9)
В уравнении (2.9) 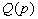 (дифференциальный оператор при выходной величине) называют собственным оператором, а
(дифференциальный оператор при выходной величине) называют собственным оператором, а 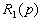 и
и 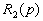 (дифференциальные операторы при входных величинах) - операторами воздействия.
(дифференциальные операторы при входных величинах) - операторами воздействия.
Передаточные функции. Отношение оператора воздействия к собственному оператору называют передаточной функцией или передаточной функцией в операторной форме. Звено, описываемое уравнением (2.6) или, что тоже самое, уравнениями (2.7)— (2.9), можно характеризовать двумя передаточными функциями: передаточной функцией 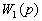 по входной величине
по входной величине 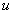 , т.е.
, т.е.
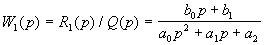 (2.10)
(2.10)
Используя передаточные функции, уравнение (2.6) записывают и передаточной функцией 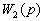 по входной величине
по входной величине 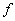 , т. е.
, т. е.
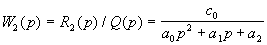 . (2.11)
. (2.11)
в виде
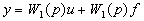 (2.12)
(2.12)
Уравнения (2.8), (2.9) и (2.12) называют уравнениями в символической или операторной форме записи.
Наряду с передаточной функцией в операторной форме широко используют передаточную функцию в форме изображений Лапласа.
Передаточные функции в форме изображений Лапласа и операторной форме с точностью до обозначений совпадают. Передаточную функцию в форме, изображения Лапласа можно получить из передаточной функции в операторной форме, если в последней сделать подстановку 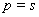 . В общем случае это следует из того. что дифференцированию оригинала —символическому умножению оригинала на
. В общем случае это следует из того. что дифференцированию оригинала —символическому умножению оригинала на 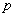 — при нулевых начальных условиях соответствует умножение изображения на комплексное число s.
— при нулевых начальных условиях соответствует умножение изображения на комплексное число s.
Сходство между передаточными функциями в форме изображения Лапласа и в операторной форме чисто внешнее, и оно имеет место только в случае стационарных звеньев (систем).
Стандартная форма записи линейных дифференциальных уравнений. Обычно линейные дифференциальные уравнения с постоянными коэффициентами не выше второго порядка записывают в стандартной форме. При этом члены, содержащие выходную величину и ее производные, записывают в левой части уравнения, а все остальные члены — в правой; коэффициент при выходной величине делают равным единице. Если в правой части содержатся производные, то члены, содержащие какую-либо одну входную величину и ее производные, объединяют в одну группу и коэффициент при соответствующей входной величине выносят за скобки. Уравнение (2.6) в стандартной форме принимает вид
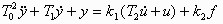 (2.16)
(2.16)
где 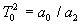 ,
, 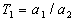 ,
, 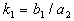 ,
, 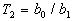 ,
, 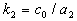 .
.
В уравнении (2.16) постоянные 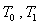 и
и 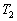 имеют размерность времени и их называют постоянными времени, а коэффициенты
имеют размерность времени и их называют постоянными времени, а коэффициенты 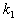 и
и 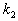 — передаточными коэффициентами. Если исходное уравнение (2.6) не содержит
— передаточными коэффициентами. Если исходное уравнение (2.6) не содержит 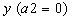 , то в стандартной форме коэффициент при производной
, то в стандартной форме коэффициент при производной 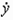 должен быть равен единице: обе части уравнения делят на коэффициент
должен быть равен единице: обе части уравнения делят на коэффициент 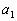 . В символической форме уравнение (2.16) принимает вид
. В символической форме уравнение (2.16) принимает вид
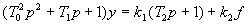 .
.
