Элементарные звенья и их характеристики
Выше звено было определено как математическая модель элемента. Вообще же звеном называют математическую модель элемента, соединения элементов или любой части системы. Звенья, как и системы, могут описываться дифференциальными уравнениями довольно высокого порядка и в общем случае их передаточные функции могут быть записаны
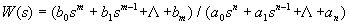 . (11)
. (11)
Но всегда их можно представить как соединения типовых или элементарных звеньев, порядок дифференциальных уравнений которых не выше второго.
Из курса алгебры известно, что полином произвольного порядка можно разложить на простые множители вида
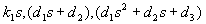 . (12)
. (12)
Поэтому передаточную функцию (11) можно представить как произведение простых множителей вида (12) и простых дробей вида
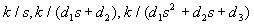 (13)
(13)
Звенья, передаточные функции которых имеют вид простых множителей или простых дробей , называют типовыми или элементарными звеньями.
Пропорциональное звено. Пропорциональным называют звено, которое описывается уравнением 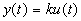 или, что то же, передаточной функцией
или, что то же, передаточной функцией 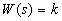 .Частотные и временные функции этого типового звена имеют вид:
.Частотные и временные функции этого типового звена имеют вид:
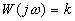 ,
, 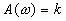 ,
, 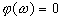 ,
, 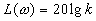 ,
, 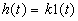 ,
, 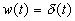 .
.
Интегрирующее звено. Интегрирующим называют звено, которое описывается уравнением 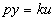 , или передаточной функцией
, или передаточной функцией 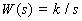 .
.
Частотная передаточная функция 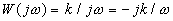 .
.
Остальные функции:
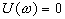 ,
, 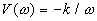 ,
, 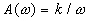 ,
, 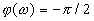 ,
, 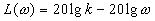 ,
, 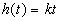 ,
, 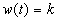 .
.
Дифференцирующее звено. Дифференцирующим называют звено, которое описывается уравнением 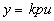 , или передаточной функцией
, или передаточной функцией 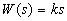 . Частотная передаточная функция имеет вид
. Частотная передаточная функция имеет вид 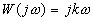 .
.
Остальные частотные и временные функции имеют вид:
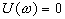 ,
, 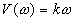 ,
, 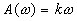 ,
, 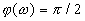 ,
, 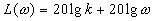 ,
, 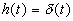 ,
, 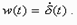 .
.
Апериодическим звеном первого порядка называют звено, которое описывается уравнением
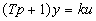 , (14)
, (14)
или передаточной функцией 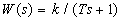 .
.
Это звено также называют инерционным звеном или инерционным звеном первого порядка. Апериодическое звено в отличие от выше рассмотренных звеньев характеризуется двумя параметрами: постоянной времени Т и передаточным коэффициентом k. Частотная передаточная функция
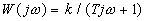 . (15)
. (15)
Умножив числитель и знаменатель на комплексно-сопряженное знаменателю число, получим
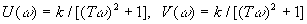 . (16)
. (16)
Тогда
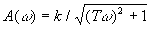 ,
, 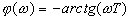 . (17)
. (17)
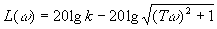 , (18)
, (18)
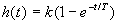 ,
, 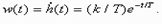 .
.
АФЧХ апериодического звена (рис. 2.7, а) есть полуокружность, в чем не трудно убедиться, исключив из параметрических уравнений (2.46) АФЧХ частоту.
ЛАЧХ представлена на рис. 2.7, б. На практике обычно ограничиваются построением так называемой асимптотической ЛАЧХ (ломаная линия на том же рис. 2.7, б).
Частоту 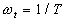 , при которой пересекаются асимптоты, называют сопрягающей частотой. Точная и асимптотическая ЛАЧХ наиболее сильно отличаются при сопрягающей частоте; отклонение при этой частоте примерно равно 3 дБ. Уравнение асимптотической ЛАЧХ имеет вид:
, при которой пересекаются асимптоты, называют сопрягающей частотой. Точная и асимптотическая ЛАЧХ наиболее сильно отличаются при сопрягающей частоте; отклонение при этой частоте примерно равно 3 дБ. Уравнение асимптотической ЛАЧХ имеет вид:
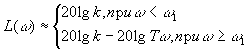 .
.
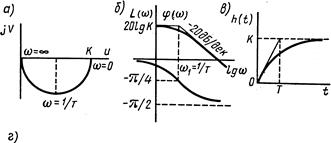
Рис. 2.7.
Оно получается из уравнения (18) , если в нем под корнем при 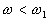 пренебречь первым слагаемым, а при
пренебречь первым слагаемым, а при 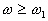 — вторым слагаемым.
— вторым слагаемым.
Форсирующим звеном или форсирующим звеном первого порядка называют звено, которое описывается уравнением 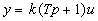 , или, что то же, передаточной функцией
, или, что то же, передаточной функцией 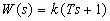 .
.
Это звено, как и апериодическое, характеризуется двумя параметрами: постоянной времени Т и передаточным коэффициентом k. Частотная передаточная функция 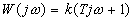 .
.
Остальные частотные и временные функции имеют вид:
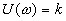 ,
, 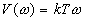 ,
, 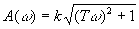 ,
, 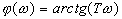 ,
, 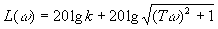 ,
, 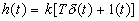 ,
, 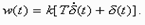 .
.
АФЧХ (рис. 2.8, а) есть прямая, параллельная мнимой оси и пересекающая действительную ось в точке U == k. ЛАЧХ изображена на рис. 2.8,б. Как и в случае апериодического звена, на практике ограничиваются построением асимптотической ЛАЧХ (ломаная линия). Частоту 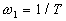 , соответствующую точке излома этой характеристики, называют сопрягающей частотой.
, соответствующую точке излома этой характеристики, называют сопрягающей частотой.
Уравнение асимптотической ЛАЧХ форсирующего звена имеет вид
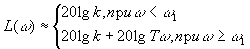 .
.
Асимптотическая ЛАЧХ при 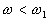 параллельна оси частот и пересекает ось ординат при
параллельна оси частот и пересекает ось ординат при 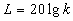 , а при
, а при 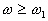 имеет наклон 20 дБ/дек.
имеет наклон 20 дБ/дек.
Колебательное, консервативное и апериодическое второго порядка звенья. Звено, которое можно описать уравнением 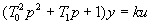 или, в другой форме
или, в другой форме
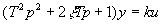 , (19)
, (19)
где 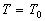 ,
, 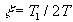 , или передаточной функцией
, или передаточной функцией
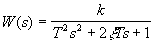 , (20)
, (20)
называют колебательным, если 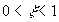 , консервативным, если
, консервативным, если 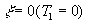 , и апериодическим звеном второго порядка, если
, и апериодическим звеном второго порядка, если 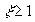 . Коэффициент
. Коэффициент 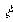 называют коэффициентом демпфирования.
называют коэффициентом демпфирования.
Колебательное звено. Частотная передаточная функция 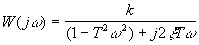 .
.
Умножив числитель и знаменатель на комплексно-сопряженное знаменателю выражение, получим вещественную и мнимую частотные функции
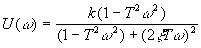 ,
, 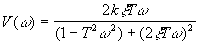
Фазовая частотная функция изменяется монотонно от 0 до 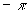 и выражается формулой
и выражается формулой
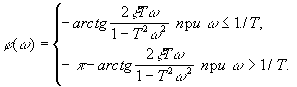
Амплитудная частотная функция
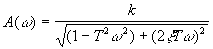
и логарифмическая амплитудная функция
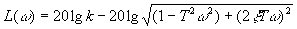 .
.
Уравнение асимптотической ЛАЧХ имеет вид
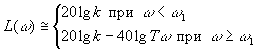 ,
,
где 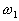 сопрягающая частота.
сопрягающая частота.
Переходная функция
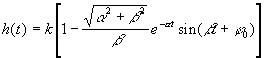 ,
,
где 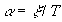 ,
, 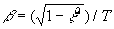 ,
, 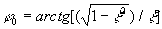 .
.
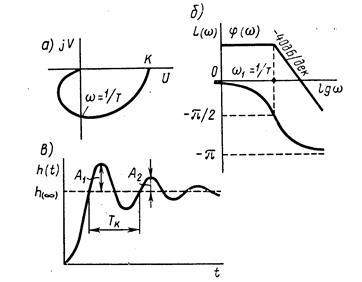
Рис. 2.9
По переходной характеристике (рис. 2.9, в) можно определить параметры колебательного звена следующим образом.
Передаточный коэффициент k определяют по установившемуся значению 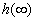 переходной функции. Постоянную времени Т и коэффициент демпфирования
переходной функции. Постоянную времени Т и коэффициент демпфирования 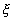 можно найти из уравнений
можно найти из уравнений
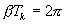 ,
, 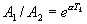
или
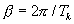 ,
, 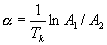 ,
,
где 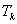 – период колебаний,
– период колебаний, 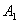 и
и 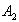 —амплитуды двух соседних колебаний относительно установившегося значения (рис. 2.9, в).
—амплитуды двух соседних колебаний относительно установившегося значения (рис. 2.9, в).
Консервативное звено ( 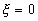 ).
).
Передаточная функция 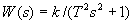 .
.
Частотная передаточная функция 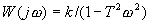 .
.
Фазовая частотная функция, как это следует из АФЧХ (рис. 2.10,а),
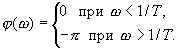
Нетрудно выписать выражения для остальных частотных функций; ЛЧХ приведены на рис. 2.10,6. Переходная функция
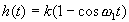 .
.
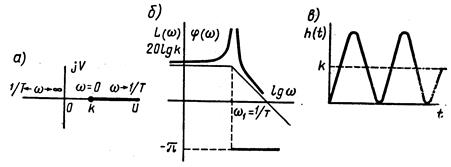
Рис. 2.10
Переходная характеристика (рис. 2.10, в) представляет собой график гармонических колебаний.
Апериодическое звено второго порядка ( 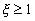 ). Передаточную функцию (20) при
). Передаточную функцию (20) при 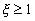 можно преобразовать к виду
можно преобразовать к виду
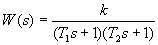 ,
,
где 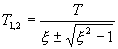 .
.
Апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка. Оно не относится к числу элементарных звеньев.
Неминимально-фазовые звенья. Звено называют минимально-фазовым, если все нули и полюса его передаточной функции имеют отрицательные или равные нулю вещественные части. Звено называют неминимально-фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.
Напомним, что нулями передаточной функции 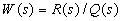 , где
, где 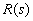 и
и 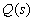 — полиномы от s. Называют корни уравнения
— полиномы от s. Называют корни уравнения 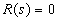 , т. е. такие значения s, при которых передаточная функция обращается в нуль, а полюсами — корни уравнения
, т. е. такие значения s, при которых передаточная функция обращается в нуль, а полюсами — корни уравнения 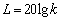 , т.е. такие значения s, при которых передаточная функция обращается в бесконечность.
, т.е. такие значения s, при которых передаточная функция обращается в бесконечность.
Все рассмотренные выше элементарные звенья относят к минимально-фазовым. Примерами неминимально-фазовых элементарных звеньев являются звенья с передаточными функциями:
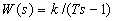 ,
, 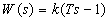 ,
,
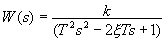 ,
, 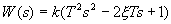
и др. Для неминимально-фазового звена характерно, что у него сдвиг фазы по модулю больше, чем у минимально-фазового звена, имеющего одинаковую с неминимально-фазовым звеном АЧХ.
На рис. 2.11 приведены ЛЧХ неминимально-фазовых звеньев с передаточными функциями 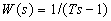 (рис. 2.11, а) и
(рис. 2.11, а) и 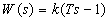 (рис. 2.11,б). ЛАЧХ этих звеньев совпадают с ЛАЧХ апериодического (рис. 2.7, б) и форсирующего (рис. 2.8, б) звеньев. Сдвиг фазы у последних меньше: фазовые частотные функции апериодического и форсирующего звеньев по абсолютной величине не превышают значения
(рис. 2.11,б). ЛАЧХ этих звеньев совпадают с ЛАЧХ апериодического (рис. 2.7, б) и форсирующего (рис. 2.8, б) звеньев. Сдвиг фазы у последних меньше: фазовые частотные функции апериодического и форсирующего звеньев по абсолютной величине не превышают значения 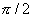 , а фазовые частотные функции соответствующих неминимально-фазовых звеньев достигают по абсолютной величине значения
, а фазовые частотные функции соответствующих неминимально-фазовых звеньев достигают по абсолютной величине значения 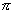 .
.
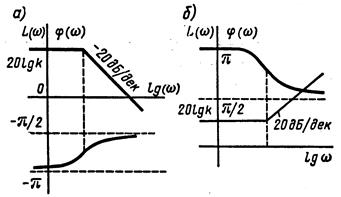
Рис. 2.11
К неминимально-фазовым звеньям относят также звено чистого запаздывания с передаточной функцией
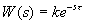 .
.
Частотная передаточная функция
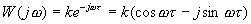 .
.
Для остальных частотных и временных функций имеем:
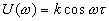 ,
, 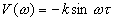 ,
, 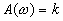 .
. 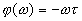 ,
, 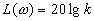 ,
, 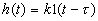 ,
, 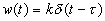 .
.
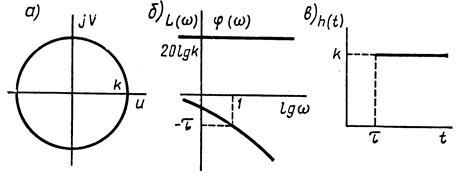
Рис. 2.12
АФЧХ (рис. 2.12, a) — окружность с центром в начале координат и радиусом k. Каждой точке этой характеристики соответствует бесконечное множество значений частот. ЛАЧХ (рис. 2.12, б) совпадает с ЛАЧХ безынерционного звена с передаточным коэффициентом k, ЛФЧХ (рис. 2.12,б)—с графиком функции 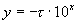 . Переходная характеристика приведена на рис. 2.12,в.
. Переходная характеристика приведена на рис. 2.12,в.
