Лекция 7 -8. Элементы векторной алгебры
Величины, например, сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
Вектор - это направленный отрезок. Если А - начало вектора, а В - его конец, то вектор обозначается символом 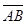 или
или  . Вектор
. Вектор 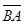 называется противоположным вектору
называется противоположным вектору 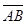 . Вектор, противоположный вектору
. Вектор, противоположный вектору  , обозначается (-
, обозначается (-  ).
).
Длиной вектора 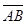 называется длина отрезка
называется длина отрезка 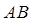 и обозначается
и обозначается 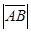 . Вектор, длина которого равна нулю, называется нулевым вектором. Для нулевого вектора направление не определено. Вектор, длина которого равна единице, называется единичным и обозначается через
. Вектор, длина которого равна нулю, называется нулевым вектором. Для нулевого вектора направление не определено. Вектор, длина которого равна единице, называется единичным и обозначается через 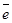 . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  . Векторы
. Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Два вектора  и
и  называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.
называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства, то есть векторы определены с точностью до параллельного переноса.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Линейные операции над векторами
Под линейными операциями над векторами обычно понимают операции сложения и умножение вектора на число.
Геометрическая интерпретация. Пусть  и
и  два произвольных вектора. Возьмем произвольную точку О и построим из нее вектор
два произвольных вектора. Возьмем произвольную точку О и построим из нее вектор 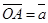 . От точки А отложим вектор
. От точки А отложим вектор 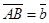 . Вектор
. Вектор 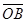 , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  и
и  :
: 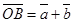
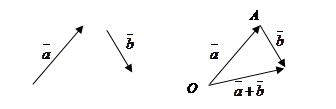
Это правило сложения векторов называется правилом треугольника. Аналогично происходит сложение нескольких векторов 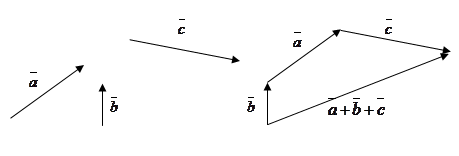
Под разностью векторов  и
и  понимается вектор
понимается вектор 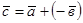 . На практике вектора
. На практике вектора  и
и  откладывают из одной точки, концы соединяют. Вектор
откладывают из одной точки, концы соединяют. Вектор 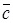 имеет направление «к концу вектора
имеет направление «к концу вектора 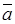 ».
».
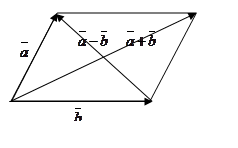
Отметим, что в параллелограмме (рис.), построенном на векторах  и
и  одна направленная диагональ является суммой векторов
одна направленная диагональ является суммой векторов  и
и  , а другая - разностью.
, а другая - разностью.
Произведением вектора  на скаляр (число) λ называется вектор
на скаляр (число) λ называется вектор 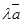 , который имеет длину вектора
, который имеет длину вектора  , умноженную на λ, а направление - совпадающее с направлением вектора
, умноженную на λ, а направление - совпадающее с направлением вектора  , если λ>0, и противоположное направлению вектора
, если λ>0, и противоположное направлению вектора  , если λ<0.
, если λ<0.
Линейные операции над векторами обладают следующими свойствами:
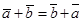 ; 2)
; 2) 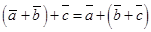 ;
;
3) 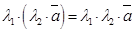 ; 4)
; 4) 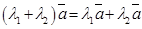 ;
;
5) 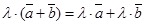 , которые вполне аналогичны свойствам элементов линейного пространства.
, которые вполне аналогичны свойствам элементов линейного пространства.
Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Оz единичные векторы (орты), обозначаемые 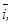
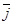 ,
, 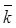 соответственно. Выберем произвольный вектор
соответственно. Выберем произвольный вектор  пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 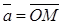 .
.
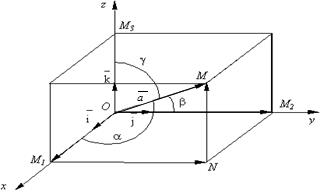 Найдем проекции вектора
Найдем проекции вектора  на координатные оси. Проведем через конец вектора
на координатные оси. Проведем через конец вектора 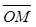 плоскости, параллельные координатным. Точки пересечения этих плоскостей с осями обозначим, соответственно, через М1, М2, М3. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
плоскости, параллельные координатным. Точки пересечения этих плоскостей с осями обозначим, соответственно, через М1, М2, М3. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 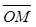 . Тогда прх
. Тогда прх  =
= 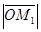 , пру
, пру  =
= 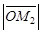 , прz
, прz  =
= 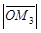 . По определению суммы нескольких векторов находим
. По определению суммы нескольких векторов находим
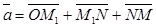 . Так как
. Так как 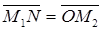 ,
, 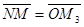 , то
, то  =
= 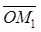 +
+ 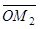 +
+ 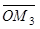 .
.
Обозначим проекции вектора  на оси соответственно через а1, а2, а3, тогда
на оси соответственно через а1, а2, а3, тогда 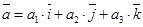 . (9)
. (9)
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а1, а2, а3 называются координатами вектора  , то есть координаты вектора есть его проекции на координатные оси.
, то есть координаты вектора есть его проекции на координатные оси.
Векторное равенство (9) часто записывают в координатном виде: 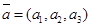 .
.
Пусть углы вектора  с осями Ох, Оу, Оz соответственно равны α, β, γ. По свойству проекции вектора на ось имеем:
с осями Ох, Оу, Оz соответственно равны α, β, γ. По свойству проекции вектора на ось имеем:
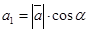 ,
, 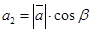 ,
, 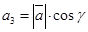 . Или, что тоже самое:
. Или, что тоже самое: 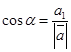 ,
, 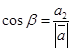 ,
, 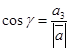 . (10)
. (10)
Числа 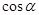 ,
, 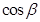 ,
, 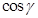 называются направляющими косинусами вектора
называются направляющими косинусами вектора  .
.
Координаты вектора.Найдем координаты вектора 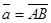 , если известны координаты точек А(х1, у1, z1) и
, если известны координаты точек А(х1, у1, z1) и
В(х2, у2, z2). Имеем: 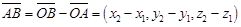 .
.
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала.
Длина вектора Если известны координаты точек А(х1, у1, z1) и В(х2, у2, z2), то длина вектора 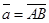 находится по формуле:
находится по формуле:
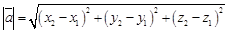 .
.
Базис системы векторов
Определение. Система векторов 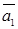 ,
, 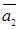 ,
, 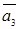 называется линейно зависимой, если существуют такие константы
называется линейно зависимой, если существуют такие константы 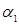 ,
, 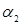 ,
, 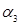 , не все не равные нулю, что имеет место равенство:
, не все не равные нулю, что имеет место равенство: 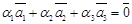 .
.
Если из этого равенства с необходимостью следует, что 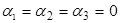 , то система называется линейно независимой.
, то система называется линейно независимой.
Определение. Базисом в 3-х мерной системе координат называется любая упорядоченная система из трех линейно независимых векторов пространства.
Теорема 1. Векторы 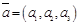 ,
, 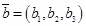 ,
, 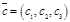 образуют базис, если D¹0, где
образуют базис, если D¹0, где 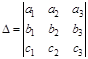 .
.
Если векторы 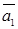 ,
, 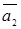 ,
, 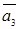 образуют базис, а вектор
образуют базис, а вектор 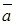 представляется в виде:
представляется в виде: 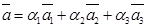 , тогда числа
, тогда числа 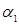 ,
, 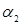 ,
, 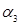 называются координатами вектора
называются координатами вектора 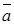 в базисе
в базисе 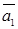 ,
, 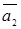 ,
, 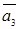 , то есть
, то есть 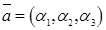 .
.
Определение. Совокупность всех 3-х мерных векторов с действительными координатами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на число, образует 3-х мерное векторное пространство.
