Свойства непрерывных функций
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций  – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.
Точки разрыва и их классификация
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел  , то функция называется непрерывной справа.
, то функция называется непрерывной справа.
Если односторонний предел  , то функция называется непрерывной слева.
, то функция называется непрерывной слева.
Определение. Точка х0 называется точкой разрывафункции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы. 
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимойточкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Основные теоремы о непрерывных функциях
Рассмотрим несколько теорем о непрерывных функциях без доказательства.
Теорема 1: сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).
Теорема 2: пусть функция  непрерывна в точке
непрерывна в точке 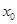 , а функция
, а функция  непрерывна в точке
непрерывна в точке  . Тогда сложная функция
. Тогда сложная функция  , состоящая из непрерывных функций, непрерывна в точке
, состоящая из непрерывных функций, непрерывна в точке 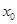 .
.
Теорема 3: если функция 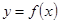 непрерывна и строго монотонна на
непрерывна и строго монотонна на 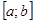 оси ОХ, то обратная функция
оси ОХ, то обратная функция  также непрерывна и монотонна на соответствующем отрезке
также непрерывна и монотонна на соответствующем отрезке  оси ОУ.
оси ОУ.
Свойства функций, непрерывных на отрезке
Теорема 1 (Вейерштрасса):если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значения.
Следствие:если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема 2 (Больцано – Коши):если функция 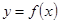 непрерывна на отрезке
непрерывна на отрезке 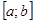 и принимает на его концах значения
и принимает на его концах значения  и
и  , то на этом отрезке она принимает и все промежуточные значения между А и В.
, то на этом отрезке она принимает и все промежуточные значения между А и В.
Следствие:если функция 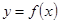 непрерывна на отрезке
непрерывна на отрезке 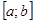 и на его концах принимает значения разных знаков, то внутри отрезка
и на его концах принимает значения разных знаков, то внутри отрезка 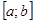 найдется хотя бы одна точка
найдется хотя бы одна точка  , в которой функция
, в которой функция 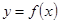 обращается в нуль.
обращается в нуль.
