Лекция 29-30. Приложения определенного интеграла
Вычисление площадей плоских фигур
Площадь криволинейной трапеции, ограниченной сверху графиком функции 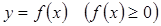 , слева и справа соответственно прямыми х=а и x=b, снизу отрезком
, слева и справа соответственно прямыми х=а и x=b, снизу отрезком 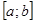 оси Ох, вычисляется по формуле
оси Ох, вычисляется по формуле 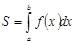 (1)
(1)
Если 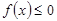 при
при 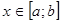 , то
, то 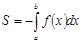 (2)
(2)
Эти формулы можно объединить в одну (3) 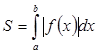
Площадь фигуры, ограниченной кривыми 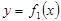 и
и 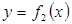 , причем
, причем 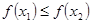 , прямыми х=а и x=b вычисляется по формуле
, прямыми х=а и x=b вычисляется по формуле 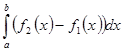 (4)
(4)
Если криволинейная трапеция ограничена кривой 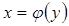 , прямыми y=c, y=d и отрезком
, прямыми y=c, y=d и отрезком 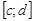 оси Оу, то её площадь вычисляется по формуле
оси Оу, то её площадь вычисляется по формуле 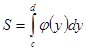 (5)
(5)
Если криволинейная трапеция ограничена сверху кривой, заданной параметрическими уравнениями 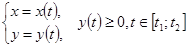 , прямыми х=а и x=b и отрезком
, прямыми х=а и x=b и отрезком 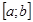 оси Ох, то её площадь вычисляется по формуле
оси Ох, то её площадь вычисляется по формуле 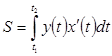 (6) где t1 и t2 определяются из равенств
(6) где t1 и t2 определяются из равенств 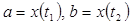 .
.
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением 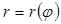 и двумя лучами
и двумя лучами 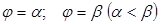 , вычисляется по формуле
, вычисляется по формуле 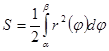 (7)
(7)
Вычисление длины дуги кривой
Пусть кривая на плоскости задана уравнением 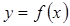 или
или 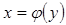 . На кривой выбраны точки А и В с координатами: А(а,с), В(c,d). Длина l дуги кривой от точки А до В вычисляется по формуле:
. На кривой выбраны точки А и В с координатами: А(а,с), В(c,d). Длина l дуги кривой от точки А до В вычисляется по формуле: 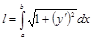 (1) и
(1) и 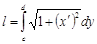 (2).
(2).
Если кривая задана параметрическими уравнениями 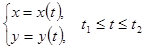 , то длина дуги вычисляется по формуле
, то длина дуги вычисляется по формуле 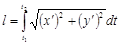 (3). Если кривая задана уравнением в полярных координатах
(3). Если кривая задана уравнением в полярных координатах 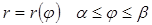 , то длина дуги кривой вычисляется по формуле
, то длина дуги кривой вычисляется по формуле 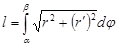 (4).
(4).
Объем тела вращения
Объем тела, образованного вращением вокруг оси Ох
криволинейной трапеции, ограниченной кривой 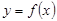 , осью Ох и двумя вертикалями х=а и x=b (рис.4), вычисляется по формуле
, осью Ох и двумя вертикалями х=а и x=b (рис.4), вычисляется по формуле 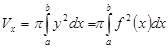 (1). Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции, ограниченной кривой
(1). Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции, ограниченной кривой 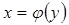 , осью Оу и двумя параллелями у=с и y=d , вычисляется по формуле
, осью Оу и двумя параллелями у=с и y=d , вычисляется по формуле 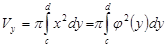
Площадь поверхности вращения
Площадь поверхности, образованной вращением вокруг оси Ох дуги кривой 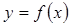 между точками с абсциссами х=а и x=b, выражается формулой
между точками с абсциссами х=а и x=b, выражается формулой 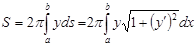 (1).
(1).
( 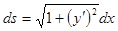 - дифференциал дуги кривой).
- дифференциал дуги кривой).
Если кривая задана параметрическими уравнениями 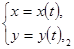 , то
, то 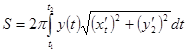 (2)
(2)
где t1 и t2- значения параметра t, соответствующие концам вращаемой дуги.
Физические (механические) приложения определенного интеграла
А) Путь, пройденный телом, перемещающимся со скоростью 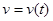 , за промежуток времени
, за промежуток времени 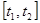 , выражается интегралом:
, выражается интегралом: 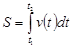
Б) Работа переменной силы, заданной функцией 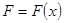 и направленной вдоль оси Ох на отрезке
и направленной вдоль оси Ох на отрезке 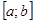 равна интегралу:
равна интегралу: 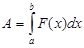
В) Давление жидкости на горизонтальную пластину равно весу столба этой жидкости («закон Паскаля»), т. е. 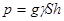 , где
, где 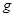 ускорение свободного падения,
ускорение свободного падения, 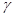 - плотность жидкости,
- плотность жидкости, 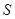 — площадь пластинки,
— площадь пластинки, 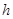 - глубина ее погружения.
- глубина ее погружения.
Давленое жидкости на вертикальную пластину, ограниченную линиями х = а, х = в, 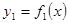 и
и 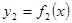 , вычисляется по формуле
, вычисляется по формуле 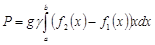
Г) Статические моменты, относительно координатных осей, моменты инерции и координаты центра тяжести плоской дуги 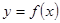 ,
, 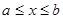 , находятся соответственно по формулам
, находятся соответственно по формулам 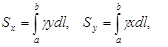
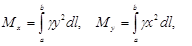 где
где 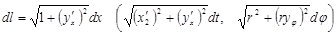 - дифференциал дуги.
- дифференциал дуги. 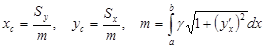 (здесь
(здесь 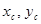 — координаты центра тяжести, а т — масса кривой).
— координаты центра тяжести, а т — масса кривой).
СЕМЕСТР
