Исследование функций с помощью пределов (асимптоты графика функции)
Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность
ü Вертикальная: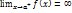 
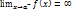, x=a
ü Горизонтальная: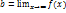 
, y=b
ü Наклонная: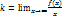 
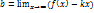, y=kx+b,если k=0, то y=b
Исследование функций с помощью производной (монотонность и экстремумы, направление выпуклости и точки перегиба).
· Монотонность: f’(x)≥0 – возрастает
f'(x)≤0 – убывает
· Экстремумы:
-max:f(x)<f(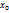 
), min:f(x)>f( )
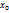-необходимое условие extr:если ф-я имеет в некоторой точке extr, то ее производная в этой точке равна нулю или не существует – критические точки
-достаточное условие extr:если при переходе через точку ф-я меняет знак с + на -, то это max, если с – на +, то это min
если ф-я имеет вторую производную и производная в точке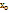 
– отрицат, то это точка max, если в 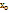– положит, то это min: y’’( 
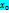)<0 – max\ y’’( 
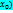>0 – min\ y’’( 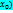=0 – нет
· Направление выпуклости:
-Если на пром-ке график лежит НЕ ВЫШЕ своих касательных, то он выпуклый вверх: f’’(x)≥0
-Если график лежит НЕ НИЖЕ своих касательных, то он выпуклый вниз: f’’(x)≤0 Точки перегиба – точки графика, где направление выпуклости меняется, y’’=0 или не сущ = критические точки второго рода
Наибольшее и наименьшее значения функции на отрезке.
Если ф-я задана на отрезке, то наиб и наим значения достигаются либо в extr, либо на границах отрезка
Функции нескольких переменных.
Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D
z=f(x,y)
Частные производные первого и второго порядков функции двух переменных.
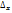– частное производное 1го порядка по х:
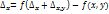
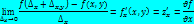
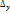– частное производное 1го порядка по у: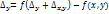 
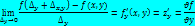
При вычислении частной производной по х (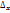 
) – переменная у считается постоянной, и наоборот, при вычислении 
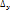– постоянная х
Частные производные 2го порядка:
; 
= 
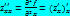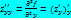
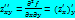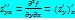- смешанные производные
Полный дифференциал функции двух переменных.
Полным дифференциалом функции переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции:
Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных:
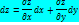
Экстремум функции двух переменных. Критические точки.
Схема нахождения extr двух переменных:
· 
, 
· 
, => ( ; 
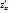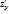
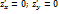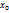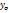) – критические точки
· 
; 
; 
· 
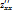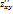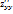
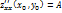
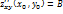
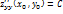
· ∆ = AC -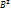 
: если ∆>0, то extr есть в т.( 
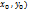\если A>0, то min\если A<0, то max
если ∆<0, то extr нет в т.(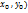 
если ∆=0, то требуется доп исследование