Линейные разностные уравнения с постоянными коэффициентами
Уравнение вида
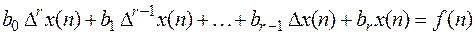 , (1)
, (1)
где 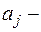 некоторые числа, называется линейным разностным уравнением с постоянными коэффициентами.
некоторые числа, называется линейным разностным уравнением с постоянными коэффициентами.
Обычно вместо уравнения (1) рассматривается уравнение, которое получается из (1) путем перехода от конечных разностей к значению функции, т. е. уравнение вида
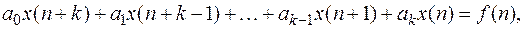 (2)
(2)
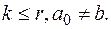
Если в уравнении (2) функция, 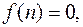 то такое уравнение называется однородным.
то такое уравнение называется однородным.
Рассмотрим однородное уравнение
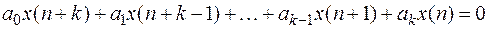 . (3)
. (3)
Теория линейных разностных уравнений аналогична теории линейных дифференциальных уравнений.
Теорема 1.
Если функции 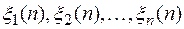 являются решениями однородного уравнения (3), то функция
являются решениями однородного уравнения (3), то функция
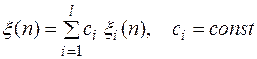
также является решением уравнения (3).
Доказательство.
Подставим функции 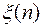 в (3)
в (3)
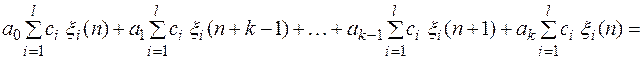
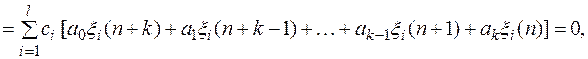
т. к. функция 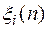 является решением уравнения (3).
является решением уравнения (3).
Решетчатые функции 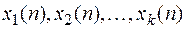 называются линейно зависимыми, если найдутся такие числа,
называются линейно зависимыми, если найдутся такие числа, 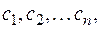 причем хотя бы одно отлично от нуля, для любого n справедливо:
причем хотя бы одно отлично от нуля, для любого n справедливо:
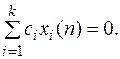 (4)
(4)
Если (4) имеет место только при 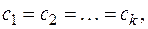 то функции
то функции 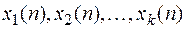 , называются линейно независимыми.
, называются линейно независимыми.
Любое k линейно независимымых решений уравнения (3) образуют фундаментальную систему решений.
Пусть 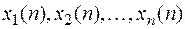 линейно независимымые решения уравнения (3), тогда
линейно независимымые решения уравнения (3), тогда
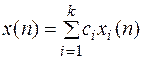
является общим решением уравнения (3). При нахождении конкретного условия, 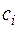 определяется из начальных условий
определяется из начальных условий 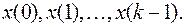
Будем искать решение уравнения (3) в виде:
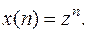
Подставим 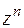 в уравнение (3)
в уравнение (3)
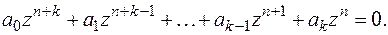 (5)
(5)
Поделим уравнение (5) на 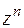
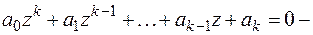 характеристическое уравнение. (6)
характеристическое уравнение. (6)
Положим, что (6) имеет только простые корни 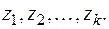 Нетрудно убедиться, что
Нетрудно убедиться, что 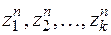 являются линейно независимыми. Общее решение однородного уравнения (3) имеет вид
являются линейно независимыми. Общее решение однородного уравнения (3) имеет вид
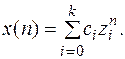
Пример.
Рассмотрим уравнение
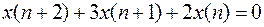
Характеристическое уравнение имеет вид
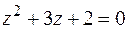
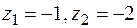
Решение имеет вид
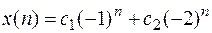 .
.
Пусть корень 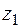 имеет кратность r. Этому корню соответствует решение
имеет кратность r. Этому корню соответствует решение
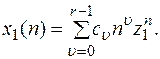
Если предположить, что остальные корни 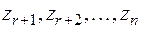 не являются кратными, то общее решение уравнения (3) имеет вид
не являются кратными, то общее решение уравнения (3) имеет вид
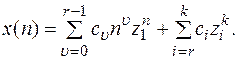
Рассмотрим общее решение неоднородного уравнения (2).
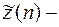 частное решение неоднородного уравнения (2), тогда общее решение
частное решение неоднородного уравнения (2), тогда общее решение
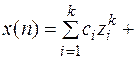
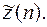
ЛЕКЦИЯ 16
План лекции
1. Понятие о D и Z - преобразованиях.
2. Область применения D и Z - преобразований.
3. Обратные D и Z - преобразования.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА.
Z – ПРЕОБРАЗОВАНИЕ.
В прикладных исследованиях, связанных с использованием решетчатых функций, широко применяется дискретное преобразование Лапласа (Д – преобразование) и Z – преобразование. По аналогии с обычным преобразованием Лапласа дискретное задается в виде
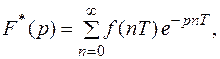 где (1)
где (1)
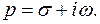
Символически Д – преобразование записывается в виде
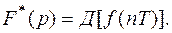
Для смещенных решетчатых функций
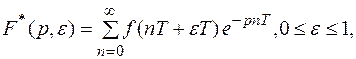 (2)
(2)
где 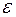 - смещение.
- смещение.
Z – преобразование получается из Д – преобразования подстановкой 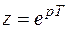 и задается соотношением
и задается соотношением
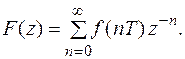 (3)
(3)
Для смещенной функции
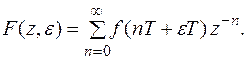
Функция 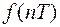 называется оригиналом, если
называется оригиналом, если
1) 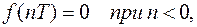
2) существует показатель роста, т. е. найдутся такие 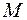 и
и 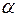 , что
, что
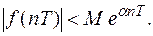 (4)
(4)
Наименьшее из чисел 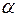 (или предел, к которому стремится наименьшее число), для которого справедливо неравенство (4), называется абсциссой абсолютной сходимости и обозначается
(или предел, к которому стремится наименьшее число), для которого справедливо неравенство (4), называется абсциссой абсолютной сходимости и обозначается 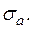
Теорема.
Если функция 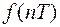 является оригиналом, то изображение
является оригиналом, то изображение 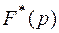 определено в области Re p >
определено в области Re p > 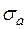 и является в этой области аналитической функцией.
и является в этой области аналитической функцией.
Покажем, что при Re p > 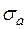 ряд (1) абсолютно сходится. Имеем
ряд (1) абсолютно сходится. Имеем
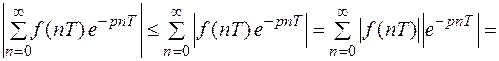
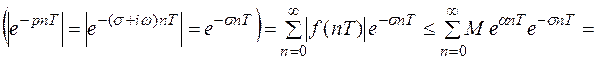
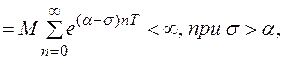
т. к. указанная сумма представляет собой сумму членов убывающей геометрической прогрессии с показателем 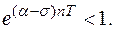 Известно, что такая прогрессия сходится. Величину
Известно, что такая прогрессия сходится. Величину 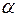 можно взять сколь угодно близкой величине
можно взять сколь угодно близкой величине 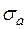 , т. е. первая часть теоремы доказана.
, т. е. первая часть теоремы доказана.
Вторую часть теоремы примем без доказательств.
Изображение 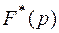 является периодической функцией с мнимым периодом
является периодической функцией с мнимым периодом 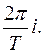
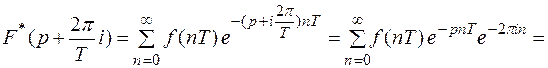
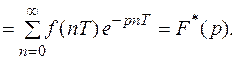
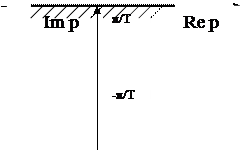
При изучении изображения 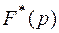 нет смысла рассматривать его на всей комплексной плоскости, достаточно ограничиться изучением в любой полосе шириной
нет смысла рассматривать его на всей комплексной плоскости, достаточно ограничиться изучением в любой полосе шириной 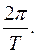 Обычно на комплексной плоскости используется полоса,
Обычно на комплексной плоскости используется полоса, 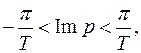 которая называется основной. Т. о. Можно считать, что изображения
которая называется основной. Т. о. Можно считать, что изображения 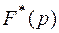 определено в полу полосе
определено в полу полосе
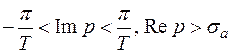 и является в этой полу полосе аналитической функцией.
и является в этой полу полосе аналитической функцией.
 |
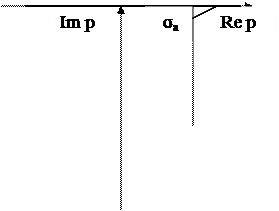 |
Найдем область определения и аналитичности функции F(z), положив 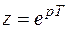 . Покажем, что полу полоса
. Покажем, что полу полоса 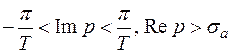 плоскости p преобразованием
плоскости p преобразованием 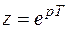 переводится в область на плоскости z:
переводится в область на плоскости z: 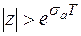 .
.
Действительно, отрезок 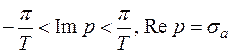 , ограничивающий полу полосу на плоскости p, переводится на плоскости z в окрестность:
, ограничивающий полу полосу на плоскости p, переводится на плоскости z в окрестность: 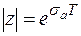 .
.
Обозначим через 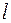 линию, в которую преобразование
линию, в которую преобразование 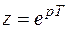 переводит отрезок
переводит отрезок 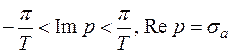 . Тогда
. Тогда
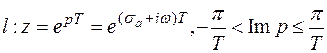
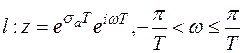
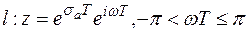
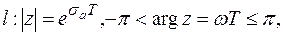 т. о.
т. о.
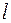 окрестность
окрестность 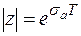 .
.
Т. о. Z – преобразование F(z) определено в области 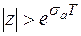 и является в этой области аналитической функцией.
и является в этой области аналитической функцией.
Обратное Д – преобразование позволяет по изображению 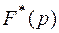 восстановить решетчатую функцию
восстановить решетчатую функцию 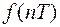
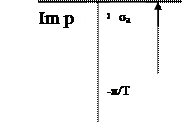 |
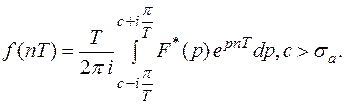 (5)
(5)  |
Докажем справедливость равенства.
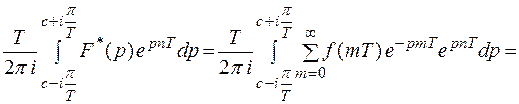
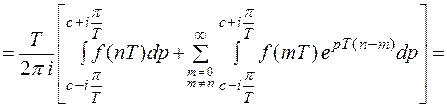
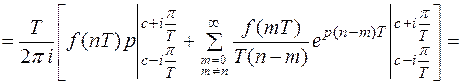
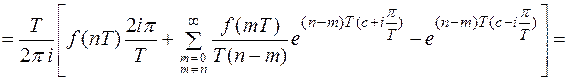
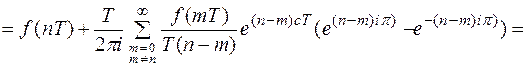
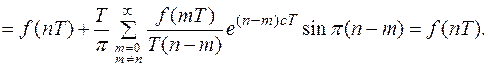
Получим из равенства (5) формулу для обратного Z – преобразования. Воспользуемся подстановкой 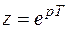 . Рассмотренным выше способом легко установить, что отрезок
. Рассмотренным выше способом легко установить, что отрезок 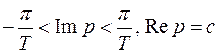 с помощью преобразования
с помощью преобразования 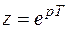 переводится на плоскости Z в окрестность
переводится на плоскости Z в окрестность 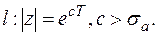
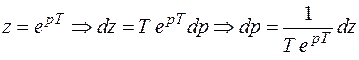 .
.
Тогда из (5) следует
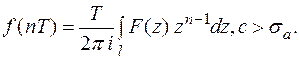 (6)
(6)
Равенство (6) задает обратное Z – преобразование, т. е. позволяет по функции F(z) восстановить решетчатую функцию f(nT).
Т. к. 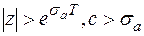 , то все особые точки функции F(z) и, следовательно, функции
, то все особые точки функции F(z) и, следовательно, функции 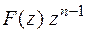 лежат внутри окрестности
лежат внутри окрестности 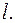
Из (6) следует, что
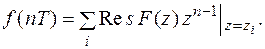
Вычеты берутся по всем особым точкам.
ЛЕКЦИЯ 17
План лекции
1. Связь между обычным преобразованием Лапласа и D и Z- преобразованиями. Преобразование 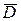 .
.
2. Основные теоремы Z - преобразования.
3. Краткий обзор содержания курса.
СВЯЗЬ МЕЖДУ ОБЫЧНЫМ ПРЕОБРАЗОВАНИЕМ ЛАПЛАСА И D И Z- ПРЕОБРАЗОВАНИЯМИ. ПРЕОБРАЗОВАНИЕ 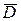 .
.
Пусть преобразование Лапласа 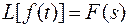 , а дискретное преобразование Лапласа
, а дискретное преобразование Лапласа 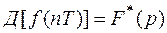 . Между преобразованием Лапласа и Д – преобразованием имеет место соотношение
. Между преобразованием Лапласа и Д – преобразованием имеет место соотношение
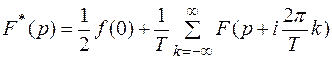 (1)
(1)
Для смещенных решетчатых функций
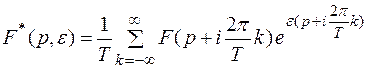 (2)
(2)
Равенства (1) и (2) позволяют установить связь между обычным преобразованием Лапласа и Z – преобразованием. Для этого достаточно положить 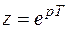 . Равенства (1) и (2) при этом принимают вид
. Равенства (1) и (2) при этом принимают вид
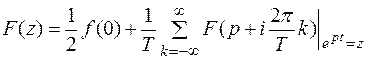 (3)
(3)
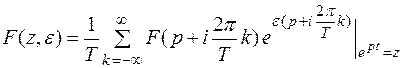 (4)
(4)
Существует более простая связь между обычным преобразованием Лапласа и Д – и Z – преобразованиями.
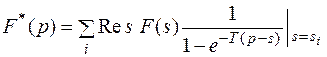 (5)
(5)
В равенстве (5) вычеты берутся по всем особым точкам функции F(s).
Для смещенных решетчатых функций
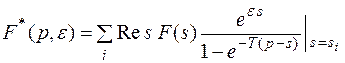 (6)
(6)
В равенстве (6) вычеты берутся по всем особым точкам функции F(s).
Для того чтобы от (5) и (6) перейти к соотношениям, связывающим обычное преобразование Лапласа с Z – преобразованием, достаточно положить 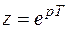 .
.
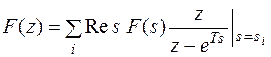 (7)
(7)
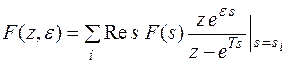 (8)
(8)
В равенствах (7) и (8) вычеты берутся по всем особым точкам функции F(s).
