Порядок выолнения работы

1. Произвести, если это необходимо, выравнивание прибора.

2. Подключить сетевой шнур прибора в сеть.

3. Нажать кнопку СЕТЬ, проверить, все ля индикаторы высвечивают цифру 0, а также .светятся ли лампочки фотоэлектрических датчиков.

4. Нижний кронштейн прибора передвинуть и зафиксировать в крайнем нижнем положении.

5. На ролик маятника положить произвольно выбранное кольцо, прижимая его до упора.

6. На ось маятника намотать нить подвески и зафиксировать ее при помощи электромагнита. Проверить, отвечает ли нижняя грань кольца нулю шкалы на колонке. Если нет, отвинтить верхний кронштейн и отрегулировать его высоту.

7. Нажать клавишу ZER – СБРОС.

8. Нажать клавишу START – ПУСК.

9. Прочитать измеренное значение времени падения маятника.

10. Определить замер времени 5 раз.

11. Определить значение среднего времени падения маятника по формуле

.

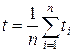12. По шкале на колонке прибора определить длину маятника.

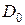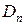13. Используя формулу (9) и известные значения диаметров и определить диаметр оси вместе с намотанной на нее нитью.

14. По формуле (8) вычислить массу маятника вместе с наложенным кольцом. Значения масс отдельных элементов нанесены на них.

15. По формуле (7) определить момент инерции маятника.

Проверка точности и правильности работы прибора

Проверка точности проводится на основании измерения рабочей погрешности определения момента инерции. Эта погрешность определяется по формуле

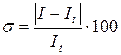%, (9)

где 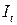– теоретическое значение момента инерции.

Теоретическое значение момента инерции

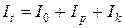, (10)

где 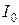– момент инерции оси маятника, 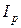– момент инерции кольца, наложенного на ролик, 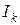– момент инерции ролика.

Значения отдельных моментов инерции:

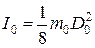, (11)

где 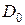– внешний диаметр оси маятника

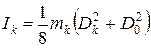, (12)

где 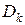– внешний диаметр ролика,

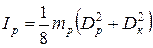, (13)

где 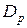– внешний диаметр кольца.

Погрешность не должна превышать 8%.

Примечание: Параметры маятника:

диаметр оси маятника 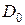– 10 мм

внешний диаметр ролика 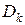– 86 мм

внешний диаметр колец 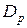– 105 мм

диаметр нити подвески 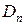– 0,5 мм

масса колец 0,25 кг

0,35 кг

0,46 кг

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Закон сохранения энергии во время движения.

2.Кинетическая энергия тела, вращающегося вокруг движущейся оси. З.Что такое момент инерции тела?

4.Какова роль момента инерции во вращательном движении?

5.Теорема Штейнера.

ЛАБОРАТОРНАЯ РАБОТА 6.

ИССЛЕДОВАНИЕ СТОЛКНОВЕНИЯ ШАРОВ

ЦЕЛЬ: проверка выполнения законов сохранения энергии и импульса при упругом и неупругом ударах.

ПРИБОРЫ: лабораторная установка ФГМ-08, набор шаров.

ОБЩИЕ УКАЗАНИЯ

Законы сохранения энергии и импульса принадлежат к фундаментальным законам природы, и их экспериментальная проверка представляет особый интерес. При изучении удара шаров это можно проделать простым и наглядным способом.

Удар – это кратковременное взаимодействие тел, при котором происходит их деформация (упругая или пластическая), а также обмен импульсом и энергией между ними.

Импульсом тела называется произведение его массы 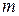на скорость :

.

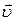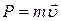Закон сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется со временем.

Математическое выражение этого закона ,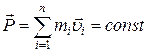

где 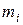, 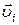– масса и скорость i-го тела системы, состоящей из тел.

Закон сохранения энергии: в замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т.е. не изменяется со временем.

До столкновения импульс системы шаров равен сумме импульсов:

,

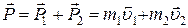или для модулей импульсов:

,

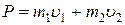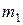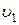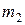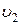где и – масса и скорость ударяющего шара; и – масса и скорость ударяемого шара.

До удара второй шар находится в покое: 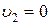и 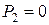, поэтому

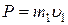. (1)

Упругий удар – это удар, при котором во взаимодействующих телах в момент удара наблюдается упругая деформация (в телах не остается после удара остаточных деформаций) и выполняются законы сохранения энергии и импульса.

После упругого удара импульс шаров:

,

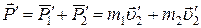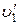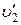где и – скорость ударяющего и ударяемого шаров сразу поело удара.

С учетом направления вектора скорости

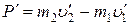. (2)

Для определения величин скоростей шаров воспользуемся следующим соображением.

В начальном положении отклоним ударяющий шар на угол 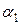. При этом центр шара поднимается на высоту

.

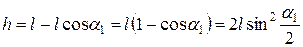Шар получит потенциальную энергию:

.

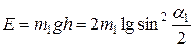Согласно закону сохранения энергии, потенциальная энергия в нижней точке перейдет в кинетическую энергию: .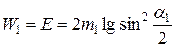

Используя определение кинетической энергии, получим:

,

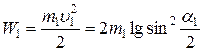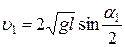. (3)

Значит, скорость ударяющего шара в нижней точке траектории зависит от начального угла отклонения .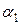

Соответственно скорости шаров после удара:

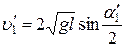, (4)

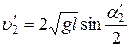, (5)

где 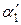– угол отклонения ударяющего шара после удара; 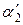– угол отклонения ударяемого шара после удара.

Абсолютно неупругийудар – столкновение тел, после которого тела движутся дальше как одно целое.

Часть энергии расходуется на пластическую деформацию, и закон сохранения энергии не выполняется.

Импульс шаров после неупругого удара

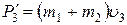, (6)

где 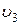– скорость шаров, движущихся вместе после неупругого удара. Общая скорость шаров

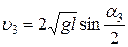, (7)

где 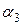– угол, на который отклонятся оба шара после неупругого удара.

Энергия шаров до удара равна кинетической энергии первого шара, поскольку второй неподвижен:

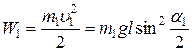. (8)

После упругого удара энергия шаров

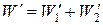, (9)

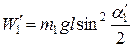, (10)

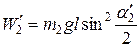. (11)

После неупругого удара энергия шаров

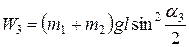. (12)