Кинетостатика начального звена
Всякий механизм с одной степенью подвижности, находящийся под действием внешних сил, считается находящимся в равновесии, если к начальному звену приложить уравновешивающую силу Fур или уравновешивающую пару сил с моментом M ур (сокращенно- уравновешивающий момент). Уравновешивающая сила Fур неизвестна по величине, известна лишь линия действия этой силы - она перпендикулярна к начальному звену.
Если механизм имеет несколько степеней свободы, то для его равновесия необходимо столько уравновешивающих сил или пар сил, сколько имеется степеней свободы. Таким образом, при силовом исследовании механизма
определяются реакции в кинематических парах и уравновешивающая сила (или уравновешивающий момент).
Пример силового расчета плоского механизма методом планов сил
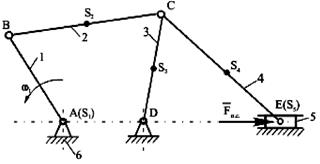
Рисунок 3.1 – план механизма
Перед силовым расчетом должно быть выполнено кинематическое исследование механизма, так как для определения сил инерции Ф2, Ф3, Ф4 и Ф5 и моментов инерции MФ2, MФ3, MФ4 нужно знать величины и направления линейных ускорений центров масс aS2 ,aS3 ,aS4 ,aE звеньев 2, 3, 4, 5, а также угловых ускорений ε2, ε3, ε4 звеньев 2, 3, 4.
Если кинематическое исследование выполнено графоаналитическим способом (методом планов скоростей и ускорений), то необходимые для силового расчета ускорения находятся из плана ускорений.
Рассчитываем силы инерции Ф2, Ф3, Ф4 и Ф5 и моменты сил инерции M2, M3, M4. Для звена 1 силами инерции можно пренебречь. Считаем, что кривошип 1 вращается равномерно (ε1 = 0 и его центр тяжести S1 совпадает с центром вращения А (aS1 = 0, поэтому Ф1 = 0 и MФ1 = 0. Ползун 5 движется поступательно, поэтому MФ5 = 0.
Силы инерции:
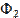 =
= 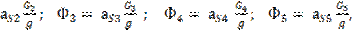
где g - ускорение свободного падения; g = 9,81 м/c2;
G2, G3, G4, G5 - силы тяжести звеньев 2, 3, 4 и 5 соответственно;
aS2 ,aS3 ,aS4 ,aS5 - ускорения центров тяжести звеньев,
величины, которых определяются при кинематическом анализе механизма.
Моменты сил инерции:
MФ2 = JS2·ε2; MФ3 = JS3∙ε3; MФ4 = JS4·ε4,
где JS2, JS3, JS4 -моменты инерции звеньев 2, 3 и 4 относительно осей, проходящих через центры тяжести S2, S3, S4;
ε2, ε3, ε4 - угловые ускорения звеньев 2, 3 и 4;
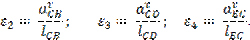
Величины и направления тангенциальных ускорений определяются при кинематическом анализе механизма.
Величины JS2 ,JS3 ,JS4 заданы. Расчленяем механизм на группы Ассура (4,5), (2,3) и начальный механизм (1,6). Силовой анализ начинаем с последней группы (4,5). Вычерчиваем в масштабе эту группу (рис.3.2). К звеньям групп прикладываем известные внешние силы G4, G5, Fn.c., а также силы инерции Ф4, Ф5 и момент инерции M4.
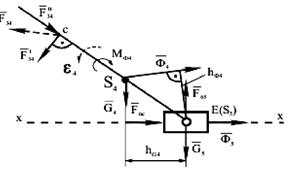
Рисунок 3.2 – группа Ассура 4,5
Вместо отброшенных звеньев 3 и 6 прикладываем силы реакции со стороны отброшенных звеньев - в шарнире С силу F3 4 и в поступательной паре (в точке Е) силу F56. При этом силу F34 раскладываем на нормальную и тангенциальную составляющие: - 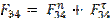
Направления составляющих выбираем произвольно.
Силы инерции Ф4 и Ф5 прикладываем в центрах тяжести S4 и S5 звеньев 4 и 5, направляя векторы этих сил противоположно векторам ускорений aS4 и aS5 .
Момент инерции MФ4 направляем противоположно направлению углового ускорения ε4 звена 4, а силу полезного сопротивления Fn.c. - противоположно направлению движения ползуна 5 (точка Е).
Составляем векторное уравнение равновесия сил группы
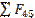 = 0;
= 0;
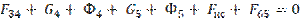
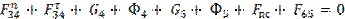
где 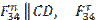 ┴ CD,
┴ CD, 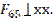
В уравнении четыре неизвестных: величина и направление силы F34, величина и точка приложения силы F65.
Для упрощения расчета точку приложения силы F65 считают известной (точка Е), тогда остается три неизвестных: величина и направление силы F43, и величина силы F65. При расчете сил пользуемся вторым уравнением.
Определяем тангенциальную составляющую из уравнения моментов всех сил, действующих на звено 4, относительно точки Е:
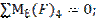
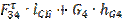 -
- 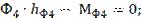
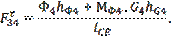
Плечи hФ4 и hG4 измеряются на чертеже группы (в мм) и умножаются на масштабный коэффициент Kl .
Если значение тангенциальной составляющей силы получится со знаком “плюс”, то это будет означать, что мы правильно выбрали направление этой составляющей, а если со знаком “минус”, то первоначально выбранное направление нужно сменить на противоположное.
После определения величины и направления тангенциальной составляющей силы остаются неизвестными величины сил Fn34 и F65 , которые находятся графическим решением уравнения -
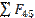 = 0.
= 0.
Сумма указанных в уравнении векторов образует замкнутый векторный контур, который называется планом сил. Для построения плана сил выбираем масштабный коэффициент сил KF , после чего определяем отрезки ( в мм), которыми будут изображаться известные силы на чертеже:
(ab) = Fτ34 /KF ; (bc) = G4 /KF ; (cd) = Ф4 /KF ;
(de) = G5 /KF ; (ef) = Ф5 /KF ; ( fh) = Fn.c./ KF .
Строим план сил (рис. 3.3). Откладываем векторы известных сил (стрелки всех векторов должны соответствовать одному и тому же обходу контура), а затем из точки h проводим направление силы F65 , а из точки а- направление силы Fn34 . Силовой многоугольник замкнется в точке K, которая будет концом вектора силы F65 и началом вектора силы Fn34.
Рисунок 3.3 – план сил структурной группы 4,5
Вектор силы Fn34 равен отрезку ka . Просуммировав векторы сил Fn34 и Fτ34 , получаем полную силу F34 , дейст-вующую на звено 4 со стороны звена 3. Определяем величины сил F34 и F65 :
F34 = kb∙KF,
F65 = hk· KF.
Теперь нужно определить реакцию в шарнире Е внутренней пары (4,5): F54 = - F4.
Эта реакция находится из уравнения суммы сил, действующих на звено 4 (или на звено 5):
F4 = 0;
F34 + G4 + Ф4 + F54 = 0.
В этом уравнении два неизвестных: величина и направление силы F54.
Для решения векторного уравнения достаточно на уже построенном плане сил (рис.6.3) соединить точки d и k.
Величина силы F54 равна:
F54 = (dk) ∙KF.
Переходим к кинетостатическому анализу группы Ассура (2,3), изображенной на рис.3.4. Масштабный коэффициент Kl при вычерчивании группы можно принять таким же, как и для группы (4,5).
Приложим силы реакции F12 и F63 в шарнирах В и D, разложив их на нормальные и тангенциальные составляющие:
Fn21, Fτ12 и Fn63, Fτ63 .
Тангенциальные составляющие найдем из уравнений моментов сил относительно точки С для звеньев 2 и 3:
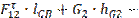
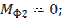
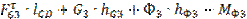 =0;
=0;
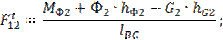
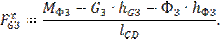
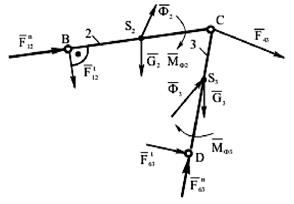
Рисунок 3.4 – структурная группа 2, 3
Если значения Fτ12 или Fτ63 получатся со знаком “минус”, то на чертеже нужно изменить направления векторов этих сил.
Для нахождения величин нормальных составляющих Fn12 и Fn63, направления которых известны, составляем векторное уравнение всех сил, действующих на группу звеньев (2,3), при этом сила Fn12 должна стоять в начале, а Fn63 - в конце уравнения:
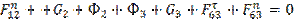
Решаем это векторное уравнение графически с помощью построения плана сил (рис. 6.5), предварительно определив отрезки (в мм), которыми будут изображаться все известные силы на плане:
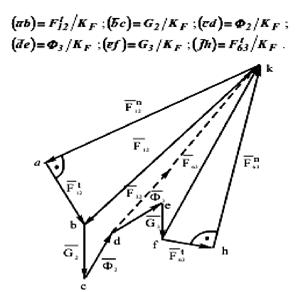
Рисунок 3.5 – план сил структурной группы 2, 3
Из плана сил находим величины сил F12 и F63 :
F12 = (bk)·KF ; F63 = (fk)∙KF .
Реакцию F32= - F23 во внутренней кинематической паре, образованной звеньями 2 и 3, найдем из условия равновесия звена 2, которое записываем в виде векторного уравнения:
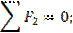
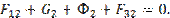
Решаем это уравнение графически. Для нахождения величины и направления реакции F32 достаточно на плане сил (рис. 6.5) соединить точки d и к. Тогда F32 = (dк)·KF .
Рассматриваем начальный механизм (рис. 6.6) и определяем силы, действующие на кривошип 1.
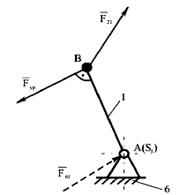
Рисунок 3.6 – начальный механизм 1,А
На кривошип 1 со стороны звена 2 действует сила F21 . Величина и направление этой силы известны: F21 = - F12, приложена она в точке В. В точке А действует сила F61 со стороны стойки 6, неизвестная по величине и направлению. В точке В также приложена уравновешивающая сила. Линия действия этой силы перпендикулярна к кривошипу, а направление вектора выбирается произвольно.
Определяем Fур из уравнения моментов сил, приложенных к звену 1, относительно точки А:
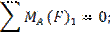
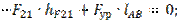
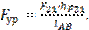
Если значение Fур получится со знаком “минус”, то нужно на чертеже изменить направление вектора уравновешивающей силы.
Заканчиваем силовой расчет определением величины и направления реакции F61, для чего составляем векторное уравнение равновесия звена 1:
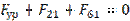
В соответствии с этим уравнением строим план сил (рис.6.7), выбрав предварительно масштабный коэффициент сил KF и определив отрезки (в мм), которыми будут изображаться силы на плане сил:
Рисунок 3.7 – план сил начального механизма
Из силового треугольника (рис.3.7) находим реакцию F61:
F61 = (ca)∙KF.
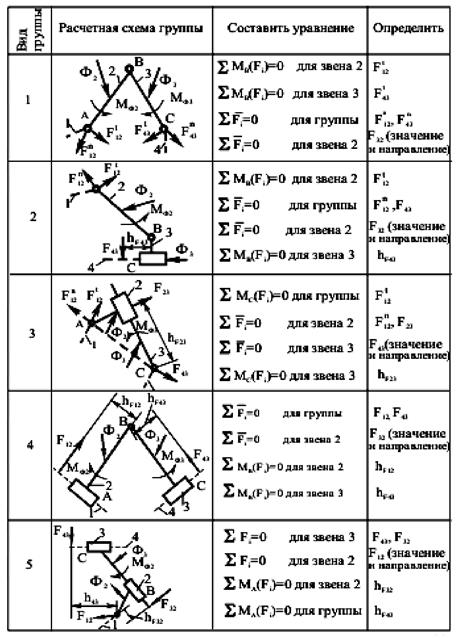
В проведенном выше кинетстатическом анализе шестизвенного механизма рассмотрена методика расчета групп Ассура второго класса первого и второго видов. Всего же, согласно классификации Ассура-Артоболевского, структурные группы второго класса подразделяются на пять видов. Методика силового расчета групп Ассура второго класса всех пяти видов приведена в таблице 3.1
Таблица 3.1 – методика силового расчета структурных групп 2 класса