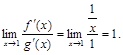Нахождение наибольшего и наименьшего значений функции на отрезке

Пусть на отрезке 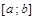задана непрерывная функция 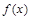, достигающая на данном отрезке своего наибольшего и наименьшего значений. Это может произойти как внутри отрезка, так и на его кон-цах. Отсюда вытекает способ нахождения точек, в которых функция приобретает наибольшее и наименьшее значение на отрезке :

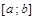1) найти критические точки функции;

2) вычислить значение функции в критических точках, которые принадлежат отрезку, и на концах отрезка;

3) наибольшее (наименьшее) значение среди образованного множества и будет наибольшим (наименьшим) значением функции, заданной на отрезке .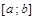

Пример 1. Найти наибольшее и наименьшее значение функции 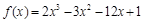на отрезке .

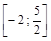Решение. Находим стационарные точки. Для этого найдем производную:

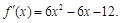
Приравнивая эту производную к нулю и решая уравнение

,

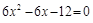получаем стационарные точки: 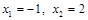. Точек, в которых функция не существует, нет.

Вычисляем значение функции в точках 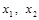, а также на концах отрезка, т.е. в точках :

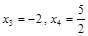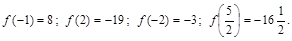
Итак, наибольшее значение 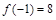, наименьшее есть .

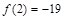Интервалы выпуклости и вогнутости кривой, точки перегиба

График функции может быть выпуклым или вогнутым.

Определение 1.График функции 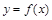называется выпуклым на интервале 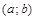, если он расположен ниже ее любой касательной на этом интервале.

Определение 2.График функции 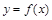называется вогнутым на интервале 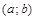, если он расположен выше ее любой касательной на этом интервале.

Интервалы выпуклости и вогнутости находят с помощью следующей теоремы:

Теорема 1. Если функция 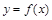во всех точках интервала 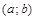имеет отрицательную вторую производную, т.е. 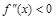, то график в этом интервале выпуклый. Если 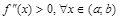– график вогнутый.

Определение 3.Точка, при переходе через которую кривая изменяет выпуклость на вогнутость или наоборот, называется точкой перегиба.

Для нахождения точек перегиба графика функции используется следующая теорема:

Теорема 2. Если вторая производная 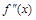при переходе через точку 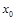, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой 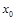есть точка перегиба.

Пример 1. Найти интервалы вогнутости, выпуклости и точки перегиба кривой, заданной уравнением .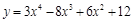

Решение. Найдем производные первого и второго порядков:

.

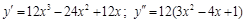Приравняем 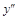к нулю:

,

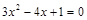отсюда находим корни:

.

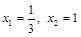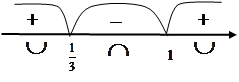Решая неравенство 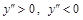с помощью метода интервалов, имеем: ,

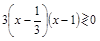таким образом, на интервалах 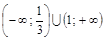производная 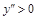, кривая вогнута, а на интервале 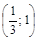кривая выпукла.

Точки 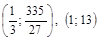есть точки перегиба кривой.

Асимптоты

Определение 1. Асимптотой кривой называют прямую, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат. Различают вертикальные, наклонные и горизонтальные асимптоты.

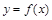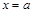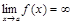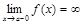Определение 2. Вертикальной асимптотой графика функции называют прямую , когда , или , или .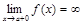

Определение 3. Наклонной асимптотой графика функци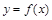и при 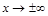называют прямую 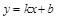, если функцию можно изобразить в ви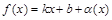де , где 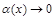, когда ( ).

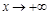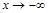Если 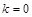, то 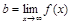. Тогда 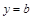– уравнение горизонтальной асимптоты.

Пример 1. Найти асимптоты графика функции .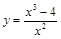

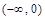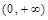Решение. Функция определена и непрерывна в интервалах и . Ось 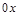функция пересекает в точке 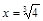. С осью 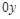точек пересечения нет. Найдем асимптоты графика функции:

1) 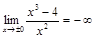, т.е. 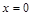— вертикальная асимптота;

2) ,

,

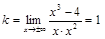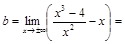
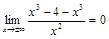итак,

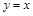
– наклонная асимптота;

3) 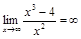, таким образом, горизонтальной асимптоты нет.

Правило Лопиталя

Правило Лопиталя-Бернулли является эффективным средством нахождения пределов функции при раскрытии неопределенностей.

Раскрытие неопределенностей типа 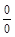или .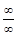

Если функци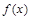и и :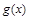

1) непрерывны и дифференцируемы в окрестности точки 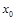, за исключением, возможно, самой точки 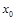, причем 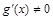в этой окрестности;

2) функци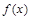и и 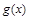есть одновременно или бесконечно малыми, или бесконечно большими при ;

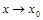3) существует конечный предел 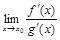, тогда:

.

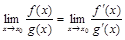Раскрытие неопределенностей типа: .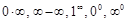

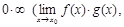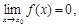
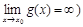1) Неопределенность когда сводится к неопределенност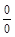и или 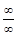таким образом:

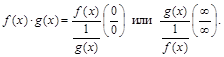
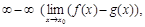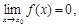
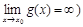2) Неопределенность когда сводится к неопределенност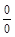и или .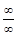

Так, например, преобразив разность функци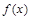й и 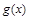в виде 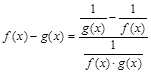, имеем неопределенность .

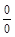3) Неопределенности типа 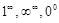сводятся к виду с помощью логарифмирования функции вида 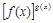или представляя функцию 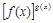в виде .

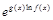Пример 1. Вычислить .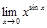

Решение. Если 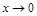, то имеем неопределенность .

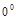Прологарифмируем:

.

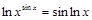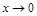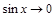Если , то , а 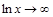. Тогда:

.

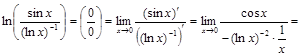
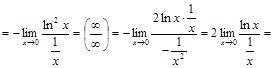
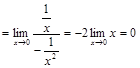Тогда .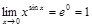

Пример 2. Вычислить предел .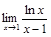

Решение. Проверим выполнение условий теоремы Лопиталя.

Пусть 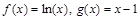. Будем рассматривать полуинтервал 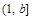, где b > 1 — произвольное число. Тогда

.

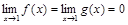Находим производные: 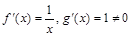для любого 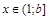, поэтому

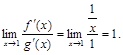
Выполняются все три условия теоремы Лопиталя. Поэтому