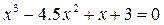Лабораторная работа №4. Решение нелинейных уравнений методом касательных
Решение нелинейных уравнений методом касательных
Краткая теория
Будем рассматривать уравнение вида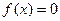 
(1).
Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом касательных. Геометрически метод касательных означает замену на отрезке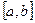 
графика функции 
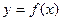касательной, проведенной через точку 
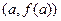или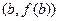 
:
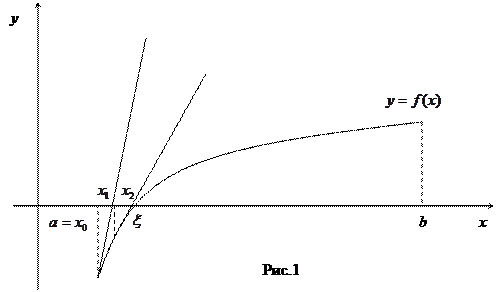
Здесь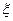 
- точный корень уравнения (1) , 
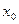- начальное приближение к корню, 
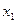- точка пересечения касательной с осью Оx – первое приближение к корню. Далее метод касательных применяется на отрезке 
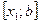и получается второе приближение корню - 
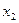. В случае, изображенном на рис.1, конец отрезка а принимает за начальное приближение к корню и касательная каждый раз проводится через левый конец отрезка. Из уравнения касательной и условия, что точка 
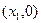принадлежит касательной, получается формула для вычисления n-го приближения к корню:
,
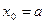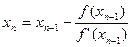(2)
Правило определения начального приближения к корню
За начальной приближение принимается тот конец отрезка, в котором знак функции совпадает со знаком её второй производной на отрезке [a,b].
Погрешность метода
Метод касательных обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длины n-го отрезка:
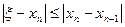
Алгоритм метода
1. Определить, какой конец отрезка принять за .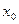
2. Вычислить новое приближение к корню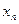 
по формуле (2).
3. Если длина отрезка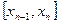 
не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять 
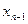или 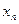, иначе идти к п.2.
Решение одного варианта
1. Отделить корни графически и уточнить их методом касательных с точностью до 0.001: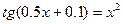 
Отделим корень графически. Построим графики функци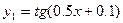й 
и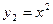 
:
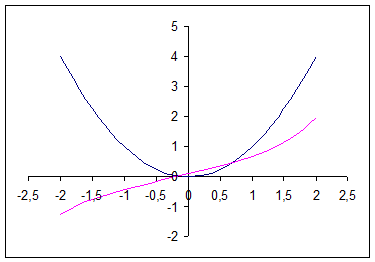
Таким образом, уравнение имеет два корня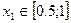 
и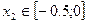 
.
Чтобы уточнить первый корень методом касательных, определим знак второй производной функции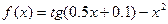 
на промежутке [0.5;1]. Имеем
;
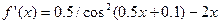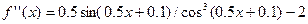
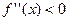при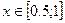 
;
, 
;
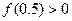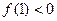следовательно, за 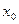следует принять правый конец отрезка: 
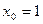. Для вычислений используем формулу (2).
Все вычисления удобно располагать в таблице:
| n | |  |  |  |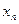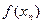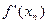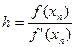
| -0.2398 | -1.1321 | 0.212 | ||
| 0.788 | -0.1272 | -0.9896 | 0.129 | |
| 0.765 | -0.0117 | -0.7991 | 0.015 | |
| 0.750 | -0.0001 | -0.7759 | ||
| 0.750 |
Второй корень вычисляется по формуле (2) при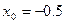 
и равен -0.144.
Ответ: x ≈ 0.750, x ≈ -0.144
2. Определить корни аналитически и уточнить их методом касательных до 0.001: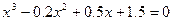 
.
Находим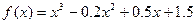 
.
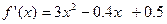
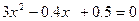
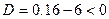Составим таблицу знаков функции f(x):
| x | - ∞ | -1 | + ∞ | ||
| Знак f(x) | - | - | + | + | + |
Из таблицы видно, что уравнение имеет один действительный корень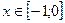 
.
Уточним корень методом касательных.
, 
,
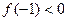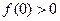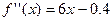
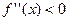при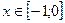
В качестве начального приближения возьмем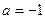 
.
Для вычислений применяем формулу (2): 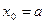, , 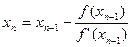где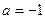
Вычисления удобно располагать в таблице:
| n | | | | |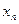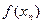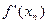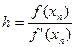
| -1 | -0.2 | 3.9 | -0.051 | |
| -0.949 | -0.009 | 3.581 | -0.003 | |
| -0.946 | 0.001 | 3.563 | ||
| -0.946 | ||||
Ответ.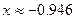 
.
Задания
1)Отделить корни графически и уточнить их методом касательных до 0.001
1. 
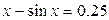
2. 
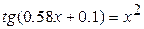
3. 
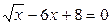
4. 
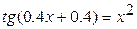
5. 
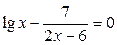
6. 
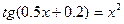
7. 
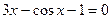
8. 
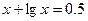
9. 
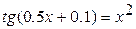
10. 
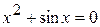
11. 
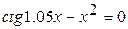
12. 
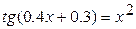
13. 
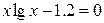
14. 
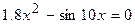
15. 
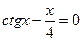
16. 
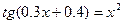
17. 
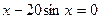
18. 
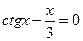
19. 
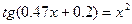
20. 
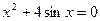
21. 
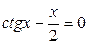
22. 
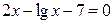
23. 
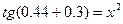
24. 
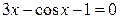
25. 
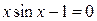
26. 
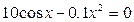
27. 
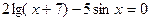
28. 
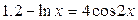
2)Отделить корни уравнения аналитически и уточнить их методом касательных до 0.001:
1. 
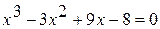
2. 
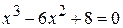
3. 
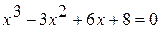
4. 
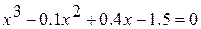
5. 
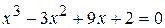
6. 
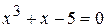
7. 
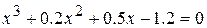
8. 
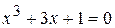
9. 
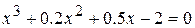
10. 
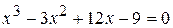
11. 
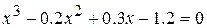
12. 
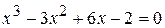
13. 
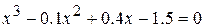
14. 
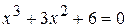
15. 
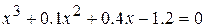
16. 
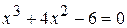
17. 
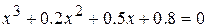
18. 
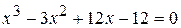
19. 
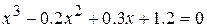
20. 
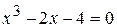
21. 
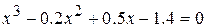
22. 
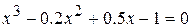
23. 
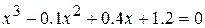
24.
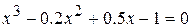
25. 
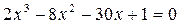
26. 
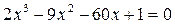
27. 
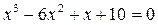
28. 