Если два события единственно возможны и несовместны, то их называют противоположными

Такие события принято обозначать, например, А и .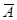

Сумма вероятностей двух противоположных событий, как следует из теоремы сложения вероятностей, равна еди­нице:

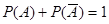(2.5)

*Проиллюстрируем справедливость (2.5) на предыдущем примере.
Пусть вынимание белого, или черного, или красного шара будет событи­ем А₁ , Р(А₁) = 7/10. Противоположным событием 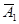является доставание синего шара. Так как синих шаров 15, а общее количество шаров 50, то получаем Р( 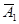) = 15/50 = 3/10 и Р(А₁) + Р( 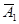) = 7/10 + 3/10 = = 1.

*В урне находятся белые, черные и красные шары. Вероятность доставания черного или красного шара равна 0,4. Найти вероятность доставания из урны белого шара.

Обозначим А событие вынимания черного или красного шара, Р(А) = 0,4; противоположным событием 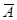будет изъятие белого ша­ра, тогда на основании (2.5) вероятность этого события Р( 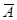) = 1 - Р(А) = = 1 - 0,4 = 0,6.

Систему событий (А₁, А₂, ... A_k) называют полной, если при испытаниях наступит одно и только одно из этих собы­тий. Сумма вероятностей событий, образующих полную сис­тему, равна единице.

* В урне имеется 40 шаров: 20 белых, 15 черных и 5 красных. Вероят­ность появления белого шара (событие А) равна Р(А) = 20/40 = 1/2, для черного шара (событие В) — Р(В) = 15/40 = 3/8 и для красного шара (со­бытие С) — Р(С) = 5/40 = 1/8. В этом случае система событий А₁, А₂, А₃ является полной; можно убедиться, что Р(А) + Р(В) + Р(С) = 1/2 + 3/8 + + 1/8 = 1.

Теорема умножения вероятностей: вероятность совместно­го появления независимых событий равна произведению их вероятностей. Для двух событий

Р(А и В) = Р(А) • Р(В). (2.6)

Докажем эту теорему. Так как события А и В независимы, то каждому из т₁ случаев, благоприятствующих А, соответствуют т₂ случаев, благоприятствующих В. Таким образом, общее число случаев, благоприятствующих совместному появлению событий А и В, равно т₁ т₂. Аналогично, общее число равновозможных собы­тий равно п₁ п₂, где п₁ и п₂ — числа равновозможных событий со­ответственно для А и В. Имеем

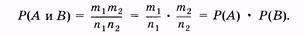(2.7)

* В одной урне находится 5 черных и 10 белых шаров, в другой 3 чер­ных и 17 белых. Найти вероятность того, что при первом вынимании ша­ров из каждой урны оба шара окажутся:

1) черными; 2) белыми; 3) в пер­вой урне будет вынут черный шар, а во второй — белый; 4) в первой урне будет вынут белый шар, а во второй — черный.

Вероятность вытаскивания черного шара из первой урны (событие А) равна Р(А) =

= 5/15 = 1/3, черного шара из второй урны (событие В) — Р(В) = 3/20, белого шара из первой урны (событие А') — Р(А') = 10/15 = 2/3 и белого шара из первой урны (событие В') — Р(В') = 17/20. Нахо­дим вероятность совместного появления двух независимых событий по формуле (2.6):

1) Р(А и В) = Р(А) • Р(В) = (1/3) (3/20) = 3/60 — оба шара черные;

2) Р(А' и В') = Р(А') • Р(В') = (2/3) (17/20) = 17/30 — оба шара белые;

3) Р(А' и В') = Р(А) • Р(В') = (1/3) (17/20)= 17/60 — в первой урне бу­дет вынут черный шар, а во второй — белый;

4) Р(А' и В) = Р(А') • Р(В) = (2/3) (3/20) = 1/10 — в первой урне будет вынут белый шар, а во второй — черный.

Все четыре возможных случая А и В, А' и В', А и В', А' и В образуют полную систему событий, поэтому

Р(А и В) + Р(А' и В') + Р(А и В') + Р(А' и В) = 3/60 + 17/30 + 17/60 + 1/10 = 1.

* Найти вероятность того, что в семье с тремя детьми все трое сыновья. Считать, что вероятность рождения мальчика равна 0,515и по каждого последующего ребенка не зависит от пола предыдущих детей.

По теореме умножения вероятностей, Р(А и В и С) = 0,515 • 0,515 • 0,515 » 0,14.

Теорема умножения вероятностей усложняется, если оп­ределяется вероятность события, состоящего из совместно­го появления двух зависимых между собой событий. В том случае, когда событие В выполняется при условии, что собы­тие А имело место, вероятность совместного появления двух этих событий равна

Р(А и В) = Р(А) • Р(В/А), (2.8)

где Р(В/А) — условная вероятность, т. е. вероятность события В при условии, что событие А состоялось.

* В урне 5 шаров: 3 белых и 2 черных. Найти вероятность того, что по­следовательно один за другим будут вынуты черный и белый шары.

Вероятность того, что первым будет изъят черный шар (событие А), равна Р(А) = т/п = 2/5. После удаления черного шара в урне остается 4 шара: 3 белых и 1 черный. В этом случае вероятность вынимания белого шара (событие В после выполнения события А) равна Р(В/А) = 3/4. Ис­пользуя (2.8), получаем

Р(А и В) = (2/5) • (3/4) = 3/10.