Частные производные первого порядка

Геометрический смысл

Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

Формула Ньютона-Лейбница или основной формулой интегрального исчисления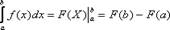

Несобственным называется определённый интеграл, если выполняется, по крайней мере, одно из следующих условий: а)Предел a или b (или оба предела) являются бесконечными;в) Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].

Геометрический смысл несобственного интеграла I рода-несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.

Геометрический смысл несобственных интегралов II рода-несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции

Несобственным интегралом (интегралом первого рода) от функции f(x) на полуинтервале [а, +∞) называется предел

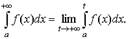
В этом случае говорят, что несобственный интеграл сходится ,в противном случае -расходящимся.

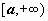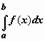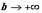Несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла при называется несобственным интегралом функции f(x) от a до 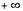и обозначается .

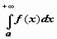Несобственным интегралом 2 рода называется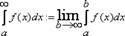

Признаки сходимости несобственного интеграла 2 рода

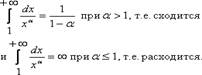
Метод замены переменной

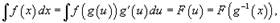замену переменной, переход от x к новой переменной u

Интегрирование по частям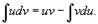

Отрезком интегрирования - отрезок[a.b] .

Если каждой упорядоченной паре чисел 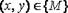по некоторому закону поставлено в соответствие единственное действительное число , то говорят, что задана функция двух переменных 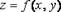или 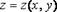. Числа называются при этом независимыми переменными или аргументами функции, а число – зависимой переменной.

Область определения функции двух переменных-область в плоскости XOY

Пусть функция f такова, что её область определения содержит целиком некоторое окончание базы b . Число L называется пределом функции f по базе b , если для любого, сколь угодно малого, числа 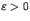найдётся такое окончание E базы b , что при всех 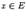выполняется неравенство 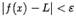. Число L обозначается тогда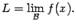

Функцией двух переменных называется соответствие ƒ, которое каждой паре чисел (х; у) є D сопоставляет одно и только одно число z є R, определенной на множестве D со значениями в Е, и записывается в виде z = ƒ(х;у) или ƒ : D → R При этом х и у -независимые переменные (аргументами),а z — зависимой переменной (функцией).

Частные производные первого порядка

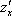или – 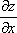частная производная по «икс»

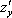или 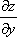– частная производная по «игрек»

Частные производные первого порядка если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M0(x0,y0,z0) к вызвавшему его приращению Δx при Δx 0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М0 и обозначается одним из символов:

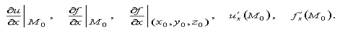
Если i=j, то есть если второе дифференцирование ведётся по той же переменной 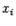, что и первое, то частная производная второго порядка 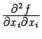называется чистой частной производной второго порядка по переменной 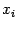и более кратко обозначается 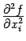. Если же 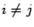, то частная производная второго порядка 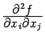называется смешанной частной производной второго порядка

Переменная z (с областью изменения Z) называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.Обозначения: z = f(x,y), z = z(x,y).

Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных в множестве М, если каждому набору чисел из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Геометрически полное приращение равно приращению аппликаты графика функции при переходе от точки в точку

Функция Z=f(x,y) называется дифференцируемой в точке P(x,y), если ее полное приращение ΔZ можно представить в виде Δz = A∙Δx+B∙Δy+ω(Δx,Δy), где Δx и Δy – любые приращения соответствующих аргументов x и y в некоторой окрестности точки Р, А и В – постоянные (не зависят от Δx,Δy), ω(Δx,Δy) – бесконечно малое более высокого порядка, чем расстояние:

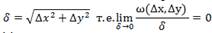
Пусть функция z =ƒ (х; у) определена в некоторой окрестности точки М(х;у). Составим полное приращение функции в точке М: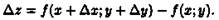

Функция z = ƒ (х; у) называется дифференцируемой в точке М(х; у), если ее полное приращение в этой точке можно представить в виде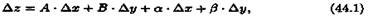

Главная часть приращение функции z=ƒ(х;у), линейная относительно Δх и Δу, называется полным дифференциалом этой функции и обозначается символом dz: dz=A*Δx+B*Δy