Решением системы являются точки пересечения графиков функции
12)
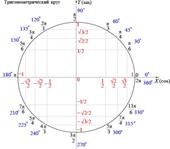
13)

14)

15) это на доске есть…
16)sin (α + β) = sin α • cos β + sin β • cos α.
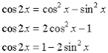
17) Сумма (и разность) тригонометрических функций преобразуется в произведение функций от других аргументов по следующим формулам, которые выводятся из теорем сложения, а также определений тангенса и котангенса:
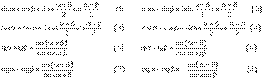
19) Простейшие тригонометрические уравнения.


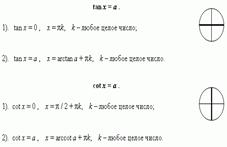
20)Основные свойства равносильности неравенств
Свойство 1. Если к обеем частям неравенства прибавить одно и то же выражение, определенное на ОДЗ исходного неравенства, то получиться неравенство, равносильное данному неравенству. Т.е. f(x) 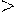 g(x)
g(x) 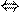
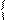 f(x)+t(x)
f(x)+t(x) 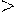 g(x)+t(x)
g(x)+t(x)  x
x 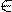 ОДЗ Если перенести слагаемые из одной части неравенства в другую, то получиться неравенство, равносильное исходному.Требование к x
ОДЗ Если перенести слагаемые из одной части неравенства в другую, то получиться неравенство, равносильное исходному.Требование к x 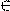 ОДЗ в следствии существенно.Если функция t(x) определена не для всех x
ОДЗ в следствии существенно.Если функция t(x) определена не для всех x 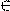 ОДЗ , то равносильность нарушена, и преобразование может привести к потере корней.
ОДЗ , то равносильность нарушена, и преобразование может привести к потере корней.
Свойство 2.Если обе части неравенства умножить или разделить на одно и то же выражение, большее нуля, определенное на ОДЗ исходного неравенства, то получиться неравенство, равносильное данному неравенству. Т.е. 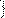 f(x)
f(x) 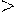 g(x) t(x)
g(x) t(x) 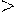 0
0 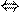
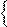 f(x)
f(x)  t(x)
t(x) 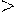 g(x)
g(x)  t(x)
t(x)  x
x 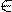 ОДЗ Замечание.Если обе части неравенства умножить или разделить на одно и то же положительное число, то получиться неравенство, равносильное данному неравенству.
ОДЗ Замечание.Если обе части неравенства умножить или разделить на одно и то же положительное число, то получиться неравенство, равносильное данному неравенству.
Свойство 3. Если обе части неравенства умножить или разделить на одно и то же выражение, меньшее нуля, определенное на ОДЗ исходного неравенства,а затем поменять знак неравенства на противоположный, то получиться неравенство, равносильное данному неравенству. Т.е. 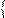 f(x)
f(x) 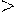 g(x) t(x)
g(x) t(x)  0
0 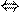
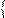 f(x)
f(x)  t(x)
t(x)  g(x)
g(x)  t(x)
t(x)  x
x 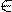 ОДЗ Замечание.Если обе части неравенства умножить или разделить на одно и то же отрицательное число, а затем поменять знак неравенства на противоположный, то получиться неравенство, равносильное данному неравенству.Пример: Решите неравенство
ОДЗ Замечание.Если обе части неравенства умножить или разделить на одно и то же отрицательное число, а затем поменять знак неравенства на противоположный, то получиться неравенство, равносильное данному неравенству.Пример: Решите неравенство 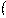 x−6
x−6 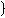 2
2 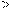
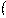 x−4
x−4 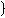 2 Решение. Преобразуем исходное неравенство и получим
2 Решение. Преобразуем исходное неравенство и получим 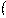 x−6
x−6 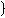 2
2 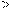
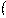 x−4
x−4 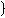 2
2 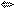
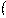 x−6
x−6 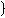 2−
2− 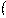 x−4
x−4 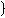 2
2 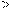 0
0 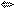 −4x+20
−4x+20 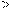 0
0 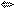 x
x 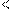 5 . Ответ: x
5 . Ответ: x 
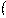 −
− 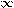 ;5
;5 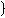
21) изи, это с дискриминантом, вроде знаю…
22) Метод Инвтервала 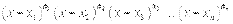 , потом кака я то фигня на плоскости строится…
, потом кака я то фигня на плоскости строится…
23) Методы решения систем уравнения.
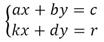
Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение. Находим решение системы.
Решением системы являются точки пересечения графиков функции.
