Основные определения и понятия

Дифференциальным уравнением называется уравнение, которое, кроме независимых переменных и неизвестных функций этих переменных, содержит производные неизвестных функций или их дифференциалы. Если функции, входящие в дифференциальные уравнения, зависят от одной переменной, то такое уравнение называется обыкновенным дифференциальным уравнением. В настоящем пособии рассматриваются лишь обыкновенные дифференциальные уравнения.

Если х - независимая переменная, у - искомая функция этой переменной, то общий вид дифференциального уравнения будет

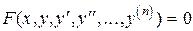. (1)

Наивысший порядок п производной неизвестной функции, входящей в уравнение, называется порядком дифференциального уравнения.

Всякая функция у = j (х), удовлетворяющая дифференциальному уравнению (1), называется решением этого уравнения. Сама задача нахождения решения называется задачей интегрирования дифференциального уравнения.

Отыскание точного или приближенного решения не всегда возможно. Например, уравнение

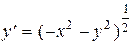
не может иметь решений, потому что правая часть его не существует при 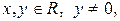х ¹ 0. Уравнение имеет единственное решение у = 0. Рассмотренные примеры показывают, что вопрос о существовании решений не очевиден. При решении подобной проблемы будем предполагать, что решение существует не в отдельных изолированных точках, а в некоторой области В.

Разыскание всех решений - основная задача теории дифференциальных уравнений. Эта задача, как правило, усложняется с ростом порядка дифференциального уравнения. Самыми простыми из дифференциальных уравнений являются уравнения первого порядка

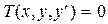, (2)

где функция 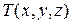и её частные производные Т_у и Т_z непрерывны на области Р точек (х,у,z) трехмерного пространства.

Общим интегралом дифференциального уравнения (2) называется связь, определенная видом

,

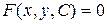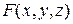( - непрерывно дифференцируема на области Р), обладающее следующим свойством: если продифференцировать его по х, считая, что у = у(х):

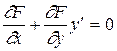
и исключить параметр С , то полученное дифференциальное уравнение эквивалентно уравнению (2).

Уравнение (2) имеет бесконечное множество решений, т.к. 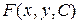содержит произвольную постоянную. Но при задании начальных условий, а именно: при заданном значении х = х_о искомая функция у принимала заданное значение у_о,

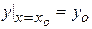, (3)

мы получим определенное решение. Для удовлетворения решения начальному условию (3) достаточно определить произвольную постоянную С из равенства

,

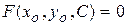если это возможно.

Решение уравнения (2) геометрически будем изображать в плоскости хОу в виде кривой. Эта кривая в каждой точке М имеет касательную и называется интегральной кривой дифференциального уравнения (2). Иными словами, каждая интегральная кривая есть линия уровня поверхности 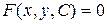с z = С, удовлетворяющей условию (3).

Положим для определенности, что уравнение (2) в заданной области В разрешено относительно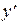

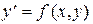. (4)

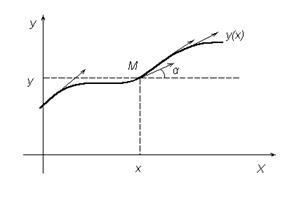Вид (4) устанавливает явную связь между координатами точки (х,у) и угловым коэффициентом 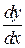к интегральной кривой в этой точке так, что

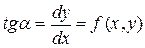(рис. А).

Каждой точке М Î В соответствует направление с угловым коэффициентом 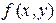. Указывая это направление единичным вектором, проходящим через точку М, получим поле направлений на В.

Для уравнения (4) имеет место теорема существования и единственности решения при заданном начальном условии.

Теорема 1.1.Если f(x,y) непрерывна по совокупности и имеет непрерывную частную производную по у в В, то через каждую точку, принадлежащую В, проходит одна и только одна интегральная кривая уравнения (4).

Если в окрестности точки М (х_о, у_о) плоскости хОу условия теоремы 1.1 не соблюдаются, то через точку М может проходить одна интегральная кривая или несколько, или бесконечное множество, а может и не существовать такой интегральной кривой. Решение дифференциального уравнения называется особым, если интегральная кривая обладает тем свойством, что через любую её точку проходит, кроме нее, еще другая интегральная кривая, касающаяся её.

Пример 1. Уравнение 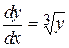определяет поле направлений на всей плоскости, но производная от правой части по у (равная 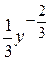) не существует при у = 0. Условие теоремы 1.1 о существовании непрерывной частной производной по у нарушается. Имеется две области у > 0 и у < 0, через каждую точку которых проходит только одна кривая

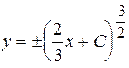. (5)

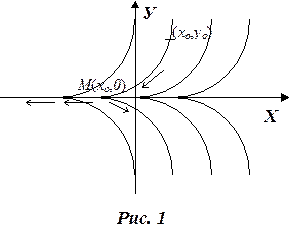Через каждую точку М (х_о, 0), кроме решения (5), проходит еще решение у = 0 и единственность решения нарушается. В целом через каждую точку плоскости проходит бесчисленное множество интегральных кривых. Если взять какую-либо точку (х_о, у_о) в верхней полуплоскости (рис. 1), то через эту точку проходит единственная кривая, не пересекающаяся с остальными интегральными линиями. Но если спуститься по этой линии до оси ОХ, то представляется бесконечное множество возможностей продолжить ее: можно спуститься вниз по кривой или пройти по оси ОХ, а затем спуститься или подняться по любой другой интегральной кривой.

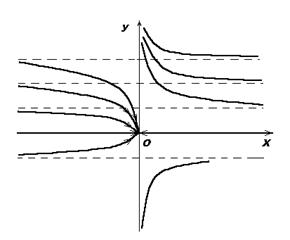
Пример 2. Рассмотрим дифференциальное уравнение 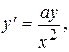где а - произвольная постоянная, отличная от нуля. Данное уравнение определяет поле направлений на всей плоскости, кроме прямой х = 0, где нарушается условие теоремы 1.1 о непрерывности правой части уравнения.

С3

С2

С1

Со= 0

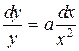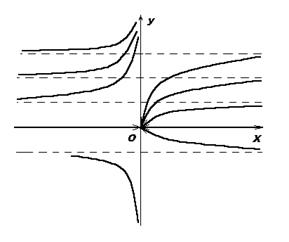
Переменные разделяются , откуда 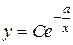. Для данного уравнения имеется две области, удовлетворяющие условию теоремы 1.1: x > 0 и x < 0. Через каждую точку плоскости, кроме (0,0), проходит одна и только одна линия семейства рис. 2 (а >0) и рис. 3

Рис. 2 Рис. 3

(а < 0). В точке(0,0), где дифференциальное уравнение не определено, все линии семейства сходятся - узловая точка интегральных линий.