Элементы финансовой математики

Эффективная процентная ставка

Рассмотрим следующую простейшую ситуацию.

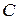Предположим, что в момент времени мы даем в долг сумму (например, кладем на свой счет в банке, вносим плату за страховку, перечисляем пенсионный взнос в пенсионный фонд и т.д.). Спустя время 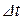мы можем рассчитывать на определенный доход 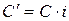от инвестирования принадлежащего нам капитала 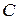. Сумма 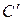является наградой за то, что наши средства использовались другим человеком. Обычно ее измеряют в относительных единицах; величина 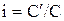называется эффективной процентной ставкой за рассматриваемый промежуток времени .

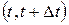Простые и составные проценты

Предположим теперь, что сумма 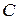может инвестироваться на два последовательных промежутка времени. Пусть 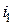– эффективная процентная ставка на первом промежутке, 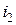– соответственно на втором. Существуют две схемы исчисления дохода 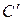на объединенном интервале:

1. Принцип простых процентов предполагает, что проценты начисляются только на основной капитал. Поэтому 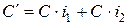. Соответственно, итоговая процентная ставка .

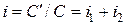2. Принцип сложных процентов предполагает, что проценты начисляются не только на основной капитал, но и на уже заработанные проценты. Поэтому в конце второго интервала времени основной капитал 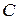вырастет до величины

.

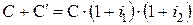Соответственно, итоговая процентная ставка 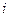определяется из условия 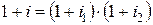, т.е. .

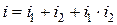Принцип сложных процентов фактически означает, что инвестор может свободно распоряжаться своими средствами. Поэтому в актуарной математике принято использовать принцип сложных процентов при определении дохода от вложенных средств.

Процентные ставки, используемые в большинстве расчетов в актуарной математике, определяются, исходя из консервативных оценок доходности реальных будущих инвестиций страховщика. Они намного ниже реальных процентных ставок, предлагаемых рынком для различных видов инвестиционных проектов. Их значение заключается в том, чтобы как-нибудь учесть рост денег, внесенных в качестве платы за страховое покрытие. Поэтому их называют техническими процентными ставками. На самом деле страховая компания зарабатывает гораздо большие проценты; более того, это один из самых (если не самый главный) источник дохода страховщика.

Накопления

Выберем некоторый промежуток времени в качестве единичного (как правило, один год) и предположим, что процентная ставка за этот промежуток равна 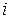. Допустим, что в момент сумма 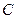инвестируется на единиц времени. По принципу сложных процентов в момент времени 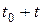капитал 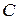превратится в сумму 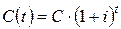. Величина 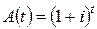называется коэффициентом накопления за время .

Интенсивность процентов

Интенсивность процентов 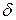– это мгновенная относительная скорость накопления средств

.

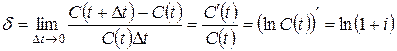Поскольку 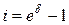, то коэффициент накопления за время можно записать в виде

.

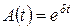Интенсивность процентов удобно использовать для изучения накоплений в случае изменяющихся процентных ставок. В этом случае 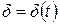и

.

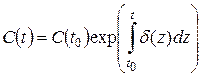Номинальные процентные ставки

Рассмотрим промежуток времени длиной 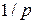. Если в качестве единицы измерения принят один год, то наиболее часто встречаются случаи: 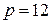(рассматриваемый промежуток времени равен одному месяцу); 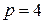(квартал); 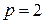(полугодие).

Эффективная процентная ставка 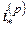за этот промежуток времени равна

.

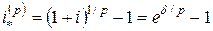Однако в финансовой математике принято характеризовать доходность вложения средств на промежутке 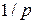не эффективной (т.е. реальной) процентной ставкой 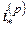, а так называемой номинальной процентной ставкой

.

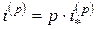Иногда величину 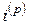называют номинальной процентной ставкой выплачиваемой (начисляемой) с частотой .

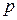Приведенная ценность

Предположим, что в момент 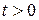в будущем мы должны будем выплатить некоторую сумму 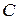. Чтобы к моменту иметь в точности сумму 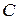в настоящее время 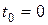нужно располагать суммой 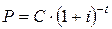, так как после инвестирования на время сумма 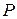превратится в сумму 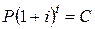. Величина 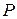называется современной ценностью суммы 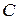в момент . Иногда употребляется термин современная стоимость, приведенная стоимость и т.д.

Величину 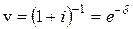называют коэффициентом дисконтирования (учета). С ее помощью формулу для приведенной стоимости можно записать в виде

.

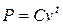Учетная ставка

Предположим, что в момент 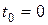мы даем взаймы сумму 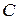. Тогда в момент 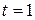нам должны вернуть сумму 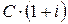, которая складывается из двух частей: возврата основного капитала 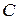и процентов на капитал .

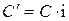Если сумму 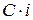, которая должна быть выплачена в момент 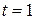, привести к моменту 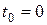, то мы получим сумму 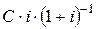. Поэтому если проценты на капитал могут быть выплачены заранее, в момент 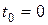получения займа, то эти проценты, выплачиваемые вперед, составляют 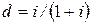от суммы займа 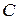. Величина 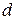называется эффективной учетной ставкой за единицу времени.

Учетная ставка 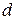может быть выражена и через интенсивность процентов 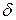и коэффициент дисконтирования :

.

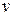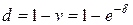Предположим теперь, что сумма 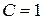дается в долг на время 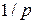с заблаговременной выплатой процентов. Эффективная процентная ставка равна 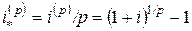. Именно эта сумма должна быть выплачена в момент 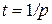в виде процентов. Если ее привести к моменту 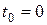, то она превратится в сумму 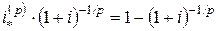. Поскольку 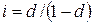, для эффективной учетной ставки 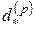за время 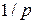получим формулу

.

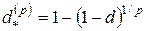Однако в финансовой математике принято работать не с эффективными (т.е реальными) учетными ставками за время 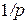, а с так называемыми номинальными (т.е. условными, не существующими реально) учетными ставками

.

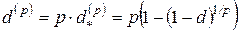Величину 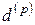называют номинальной учетной ставкой, начисляемой с частотой .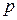