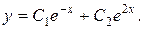Линейные однородные дифференциальные уравнения второго порядка
С постоянными коэффициентами
Рассмотрим частный случай ДУ (8.12), когда коэффициенты уравнения р и g являются постоянными величинами. Таким образом, дано линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка
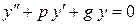 , (8.17)
, (8.17)
где р и g постоянны.
Это равнение может иметь множество решений, однако среди них необходимо выделить два линейно независимых (базисных) решений.
Будем искать решение уравнения (8.17) в виде 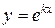 , где k - некоторое число. Подставляя эту функцию в уравнение, получаем:
, где k - некоторое число. Подставляя эту функцию в уравнение, получаем:
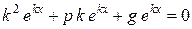
и после сокращения этого равенства на 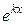 , найдём, что число k должно удовлетворять уравнению
, найдём, что число k должно удовлетворять уравнению
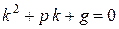 . (8.18)
. (8.18)
Уравнение (8.18) называется характеристическим уравнением для дифференциального уравнения (8.17).
При решении характеристического уравнения может представиться три случая.
С л у ч а й 1. Дискриминант характеристического уравнения (8.18) 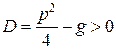 , в этом случае уравнение (8.18) имеет два неравных действительных корня k1 и k2 (
, в этом случае уравнение (8.18) имеет два неравных действительных корня k1 и k2 ( 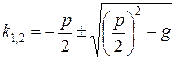 ). И частными решениями уравнения (8.17) являются функции
). И частными решениями уравнения (8.17) являются функции 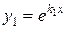 и
и 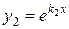 . Они образуют базисную систему решений (линейно независимы), т.к. их вронскиан
. Они образуют базисную систему решений (линейно независимы), т.к. их вронскиан
W(x) = 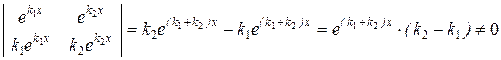 .
.
Следовательно, общее решение уравнения (8.17) имеет вид
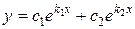 . (8.19)
. (8.19)
С л у ч а й 2. Дискриминант характеристического уравнения (8.18) 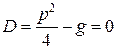 , в этом случае уравнение (8.18) имеет два равных корня k1 = k2 =
, в этом случае уравнение (8.18) имеет два равных корня k1 = k2 = 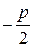 . И частным решением является лишь одно решение
. И частным решением является лишь одно решение 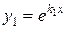 . Покажем, что наряду с
. Покажем, что наряду с 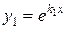 решением уравнения (8.17) будет также функция
решением уравнения (8.17) будет также функция 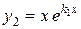 . Действительно, подставим функцию
. Действительно, подставим функцию 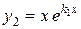 в дифференциальное уравнение (8.17).
в дифференциальное уравнение (8.17).
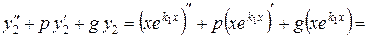
= 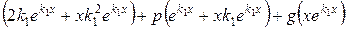 =
=
= 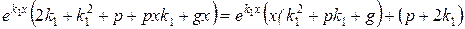 .
.
Но 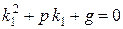 , т.к. k1 есть корень уравнения (8.18);
, т.к. k1 есть корень уравнения (8.18); 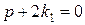 , т.к. k1 =
, т.к. k1 = 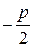 . Поэтому
. Поэтому 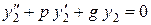 , т.е функция
, т.е функция 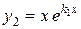 является ре-шением уравнения (8.17).
является ре-шением уравнения (8.17).
Частные решения 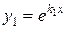 и
и 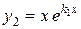 образуют базисную систему решений: определитель Вронского W(x) =
образуют базисную систему решений: определитель Вронского W(x) = 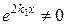 . Следовательно, в этом случае общее решение ЛОДУ является функция
. Следовательно, в этом случае общее решение ЛОДУ является функция
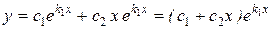 . (8.20)
. (8.20)
С л у ч а й 3. Дискриминант характеристического уравнения (8.18) 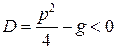 , в этом случае уравнение (8.18) имеет два комплексных корня k1 =
, в этом случае уравнение (8.18) имеет два комплексных корня k1 = 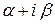 и k2 =
и k2 = 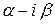 (
( 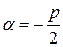 ,
, 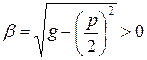 ). И частными решениями уравнения (8.17) являются функции
). И частными решениями уравнения (8.17) являются функции 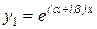 и
и 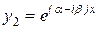 . В этом случае легко убедиться, что функции
. В этом случае легко убедиться, что функции 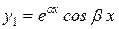 и
и 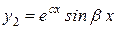 являются решениями уравнения (8.17) и образуют базисную систему решений. Прежде всего, убедимся, что эти функции
являются решениями уравнения (8.17) и образуют базисную систему решений. Прежде всего, убедимся, что эти функции 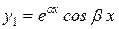 и
и 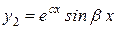 являются решениями дифференциального уравнения (8.17). Подставим значение
являются решениями дифференциального уравнения (8.17). Подставим значение 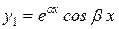 в уравнение:
в уравнение:
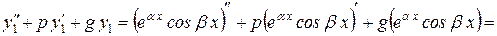
= 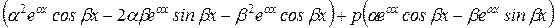 +
+
+ 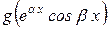 =
= 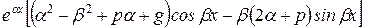 .
.
Но 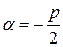 и
и 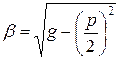 , тогда
, тогда 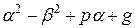 = 0 и
= 0 и 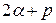 = 0. Поэтому
= 0. Поэтому 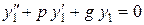 , т.е функция
, т.е функция 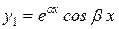 является решением уравнения (8.17). Аналогичным образом доказывается, что функция
является решением уравнения (8.17). Аналогичным образом доказывается, что функция 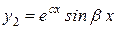 также есть решение уравнения (8.17). Кроме того, эти функции
также есть решение уравнения (8.17). Кроме того, эти функции 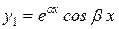 и
и 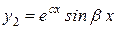 являются линейно независимыми: их вронскиан W(x) =
являются линейно независимыми: их вронскиан W(x) = 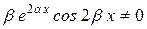 . Таким образом, общее решение уравнения (8.17) в данном случае запишется в виде
. Таким образом, общее решение уравнения (8.17) в данном случае запишется в виде
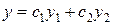 =
= 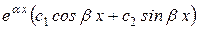 (8.21)
(8.21)
Примеры.
1. Решить уравнение 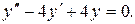
Характеристическое уравнение: 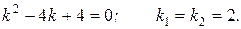
Общее решение: 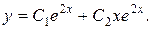
2. Решить уравнение 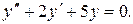
Характеристическое уравнение:
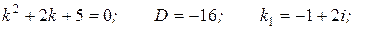
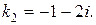
Общее решение: 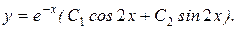
2. Решить уравнение 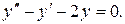
Характеристическое уравнение: 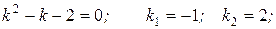
Общее решение: