Вычисление определенного интеграла
Рассмотрим интеграл 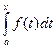 с переменным верхним пределом
с переменным верхним пределом 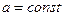 . Обозначим
. Обозначим 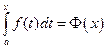 . Производная функции
. Производная функции 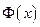 по переменному верхнему пределу х имеет вид:
по переменному верхнему пределу х имеет вид:
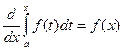 .
.
Аналогичная формула справедлива и для случая переменного нижнего предела.
Теорема. Для всякой функции 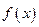 , непрерывной на отрезке
, непрерывной на отрезке 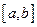 , существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
, существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема. (Теорема Ньютона – Лейбница) Если функция 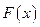 – произвольная первообразная от непрерывной функции
– произвольная первообразная от непрерывной функции 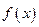 , то
, то
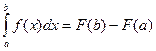
это выражение известно под названием формулы Ньютона – Лейбница.
Доказательство. Пусть 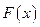 – произвольная первообразная функции
– произвольная первообразная функции 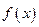 на отрезке
на отрезке 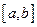 . Тогда в соответствии с приведенной выше теоремой, функция
. Тогда в соответствии с приведенной выше теоремой, функция 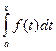 также
также
является первообразной для функции 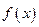 на этом отрезке. Так как любые две первообразные непрерывной функции могут отличаться только на постоянную, то
на этом отрезке. Так как любые две первообразные непрерывной функции могут отличаться только на постоянную, то
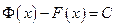 или
или 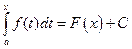 .
.
При соответствующем выборе С это равенство справедливо для любого х, т.е. при 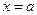 :
:
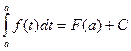
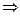
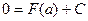
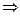
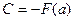 .
.
Тогда 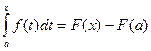 . А при
. А при 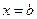 :
: 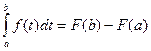 .
.
Заменив переменную 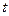 на переменную х, получаем формулу Ньютона – Лейбница:
на переменную х, получаем формулу Ньютона – Лейбница:
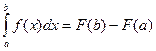 .
.
Теорема доказана.
Иногда применяют обозначение 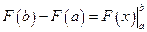 .
.
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подынтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.
Замена переменных в определённом интеграле
Пусть дан интеграл 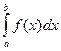 , где
, где 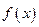 – непрерывная функция на отрезке
– непрерывная функция на отрезке 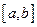 .
.
Введем новую переменную в соответствии с формулой 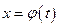 . Тогда если
. Тогда если
1) 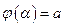 ,
, 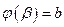
2) функции 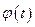 и
и 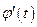 непрерывны на отрезке
непрерывны на отрезке 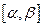
3) функция 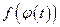 определена на отрезке
определена на отрезке 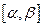 , то
, то
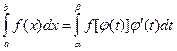 .
.
Тогда 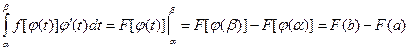
Пример.
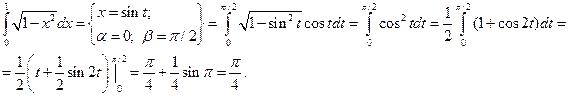
При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.
Пример.
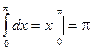 , с другой стороны, если применить тригонометрическую подстановку,
, с другой стороны, если применить тригонометрическую подстановку,
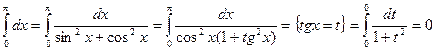 ,
,
т. е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная 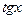 имеет на отрезке интегрирования разрыв (в точке
имеет на отрезке интегрирования разрыв (в точке 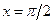 ). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
