Функциональный ряд. область сходимости функционального ряда

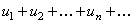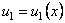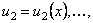
Ряд называется функциональным, если его члены являются функциями от х, т.е . , , 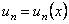которые определены на некотором множестве X.

Если переменной 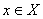придавать различные числовые значения, то будут получаться сходящиеся или расходящиеся числовые ряды. Совокупность таких значений переменной х, при которых функциональный ряд сходится, называют областью сходимости. Областью сходимости ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.

По аналогии с числовыми рядами определяются частичные суммы функционального ряда, предел которых определяет сумму ряда (если существует). Очевидно, что сумма функционального ряда в области сходимости является функцией от х, т.е.

.

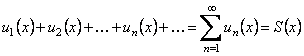Говорят, что последовательность функций 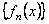сходится равномерно к функции 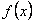на множестве D, если для любого 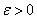можно определить такой номер N, зависящий только от 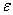, что для любого 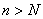и для всех 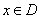выполняется неравенство

.

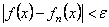Ряд 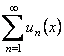сходится равномернона множестве D к сумме 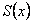, если последовательность его частичных сумм 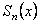сходится равномерно на множестве D к функции .

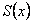Степенной ряд. Интервал и радиус сходимости степенного ряда.

Степеннымрядом называется функциональный ряд вида:

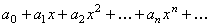(1)

где 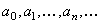– постоянные числа, называемые коэффициентами ряда.

Теорема (Абеля)

1) Если степенной ряд сходится при некотором значении 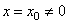, то абсолютно сходится при всяком значении 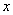, для которого справедливо .

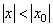2) Если степенной ряд расходится при некотором значении 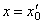, то он расходится при всяком : .

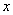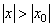Заметим, что теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Действительно, если точка х0 – точка сходимости, то интервал 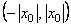заполнен точками абсолютной сходимости. Если 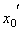– точка расходимости, то вся бесконечная полупрямая вправо от точки 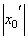и вся полупрямая влево от точки – 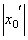состоит из точек расходимости. Из этого можно заключить, что существует число R>0, что при 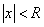мы имеем точки абсолютной сходимости, а при 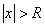– точки расходимости.Интервалом сходимости степенного ряда называется такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится при том абсолютно, а для точек х, лежащих вне его, ряд расходится (рис. 1). Число Rназывается радиусом сходимости степенного ряда.

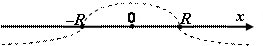
Рис. 1. Интервал сходимости степенного ряда

На концах интервала (т.е. при х = R, х = –R) вопрос о сходимости или расходимости остается не ясным. И для конкретного ряда решается индивидуально. Отметим, что у некоторых рядов интервал сходимости вырождается в точку R = 0, у других охватывает всю ось (R = ¥).