Пример построения математической модели и ее исследования

Задание: Cоставить математическую модель промышленного паронагревателя марки ПН 34-16-4 и исследовать ее при следующих условиях: возмущающее воздействие имеет вид ……., варьируемые значения параметров - ……; управляющее воздействие имеет вид ……., варьируемые значения параметров - ……

Рассмотрим паронагреватель марки ПН, предназначенный для подогрева воды насыщенным паром. Его чуть упрощенная конструкция изображена на рис. 4.1, а технические характеристики – в следующей таблице:

Поверхность нагрева, м² ……………………….. 34

Расход воды, т/час ………………………………. 50 – 100

Рабочие параметры

по пару:

давление, атм …………………………………….. 3 – 5

температура, 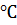………………………………….. 240 – 400

по воде:

давление, атм …………………………………….. до 10

температура, 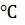………………………………… до 200

Количество трубок ……………………………. 256

Размер трубки, мм ………………………………. 16 х 1

Число ходов воды ……………………………….. 4

Вес (корпус – нерж. сталь, трубки – латунь)

сухой, т …………………………………………. 2,068

заполненный водой при 10 атм, т ……………. 3,678 (2.678)

Подсоединения:

Вход питательной воды ………………………….. А

Выход питательной воды ……………………….. Б

Вход пара ………………………………………… В

Выход конденсата ………………………………… Г .

Как видим из таблицы, в технических характеристиках не приведен целый ряд необходимых для построения математической модели параметров: температуры питательной воды на входе в аппарат и выходе из аппарата, расход пара, температура окружающей среды, в которой аппарат эксплуатируется. Значения одних придется брать из принимаемого регламентного режима, других – определять расчетным путем.

Исходя из диапазонов значений величин паспортных данных ПН 34 – 16 - 4, в качестве регламентных значений примем:

- для расхода воды – G_в0= 72 т/час (это 20 кг/с),

- для температуры пара при давлении 4 атм - t_п0 = 300 ,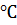

- для температуры питательной воды на входе при давлении 6 атм - t₁₀ = 20 ,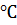

- для температуры питательной воды на выходе - t₂₀ = 150 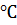(она принята близкой к температуре кипения при 6 атм, как это применяется на практике),

- для температуры окружающей среды - t_ос.0 = 20 .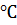

В соответствии с конструкцией аппарата, расчетная его схема изобразится так, как показано на рис. 4.2. Технологический процесс в аппарате есть теплообмен теплоносителей через стенки латунных трубок, а теплота, выделяющаяся при конденсации пара, расходуется на нагрев воды и элементов конструкции самого аппарата.

Введем в рассмотрение следующие величины, участвующие в процессе передачи тепла от горячего носителя – пара к холодному носителю – питательной воде :

- расход воды на входе – G₁ , кг/с;

- температура воды на входе – t₁, ;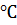

- расход нагретой воды на выходе – G₂ , кг/с (естественно, G₂= G ₁= G_в );

- температура нагретой воды на выходе – t₂, ;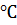

- расход пара при температуре 300 ◦С и давлении 4 атм – G_п , кг/с;

- расход конденсата с температурой t_к = 143 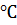– G_к , кг/с;

-расход теплоты в аппарате на нагрев находящейся в нем воды – Q_в, кДж/с;

- расход теплоты в аппарате на нагрев латунных трубок – Q_т, кДж/с;

- расход теплоты, вносимой в аппарат паром – Q_п, кДж/с;

- расход теплоты, вносимой в аппарат с водой – Q₁, кДж/с;

- расход теплоты, уносимой из аппарата с водой – Q₂, кДж/с;

- расход теплоты, уносимой из аппарата с конденсатом– Q_к, кДж/с;

- расход теплоты, передаваемой аппаратом в атмосферу– Q_пот, кДж/с.

По условиям протекания установившегося процесса логично допустить, что такие параметры нагреваемой воды, как ее объем V в аппарате, плотность ρ_в и теплоемкость c_в остаются постоянными, а при полной конденсации пара G_к = G_п . Поскольку толщина стенок латунных трубок по паспорту всего 1 мм, то мы не внесем большой погрешности, посчитав значение температуры воды в аппарате и самих стенок равной средней температуре воды на входе и выходе, то есть t_в = t_ст = 0,5(t₁ + t₂). Для составления математической модели дополнительно примем следующие допущения: t_п = const и t₁ = const .

Физические зависимости между рассматриваемыми величинами будем использовать по мере возникновения в них надобности.

В результате рассмотрения технологического процесса в аппарате, условий его протекания и сделанных допущений переменным величинам в процессе разумно сделать следующие назначения:

- управляемая величина - t₂, так как этот параметр существенно влияет на затраты энергии в последующих операциях с нагретой водой (как правило – генерация и перегрев пара),

- возмущающая величина - G_в, так как количество нагретой воды определяет производительность по пару в дальнейшем,

- управляющая величина - G_п , так как пар низкого давления относительно дёшев. Формально последние два назначения можно поменять местами.

Теперь, когда все формальности выполнены, можем составить уравнение энергетического (теплового) баланса для прихода-расхода тепла (в кДж/с) в аппарате при его функционировании в установившемся режиме.

Q_в = Q_п + Q₁ – Q_т – Q₂ - Q_к - Q_пот. , (4.1)

где входящие в уравнение величины уже были описаны при их включении в перечень рассматриваемых, а знаки слагаемых соответствуют приходу тепла в аппарат (+) и его расходу (-).

С возникновением возмущающего воздействия, за время Δτ все остальные слагаемые уравнения статики (установившегося режима) получат свои отклонения (приращения), а уравнение в приращениях запишется в виде

ΔQ_в = (ΔQ_п + ΔQ₁ – ΔQ_т – ΔQ₂ - ΔQ_к - ΔQ_пот)·Δτ. (4.2)

Каждое из этих приращений будем оценивать отдельно, начиная с теплоты, постоянно находящейся в аппарате.

Q_в = V·ρ_в· c_в·(t_в –t₁) , (4.3)

а если, как решили при анализе процесса, считать t_в = 0,5(t₁ + t₂), то

Q_в = 0,5 V·ρ_в· c_в·(t₂ –t₁). С учетом допущения о том, что t₁ = const, Q_в = Q_в(t₂). Поэтому Δ Q_в = 0,5 V·ρ_в· c_в·Δt₂. (4.4)

По закону Ньютона-Рихмана Q_т = α·F_т·( t_к - t_ст). (4.5)

Но t_к = const и t₁ = const, поэтому Q_т = Q_т (t₂) и

ΔQ_т = -0,5α·F_т·Δt₂. (4.6)

Переходим к оценке теплоты, приходящей в аппарат.

Q_п = i_п· G_п . (4.7)

Значения i_п при различных давлениях табулированы: при давлении 4 атм i_п = 2744 кДж/кг. Поэтому Q_п = Q_п (G_п) и ΔQ_п = i_п· ΔG_п. (4.8)

Q₁ = c_в· G_в· t₁. (4.9)

С учетом допущений c_в = const и t₁ = const, Q₁ = Q₁(G_в) и

ΔQ₁ = c_в · t₁₀ ·ΔG_в. (4.10)

Из аппарата уходят:

Q₂ = c_в· G_в·(t₂ –t₁). (4.11)

С учетом допущений Q₂ = Q₂(G_в, t₂) и

ΔQ₂ = c_в·(t₂₀ –t₁₀) · ΔG_в + c_в· G_в0·Δ t₂; (4.12)

Q_к = с_к · t_к · G_к . (4.13)

Конденсат есть вода. Поэтому с_к = const. Кроме того, по допущению о полной конденсации пара G_к = G_п . Тогда Q_к = Q_к (G_п ) и

ΔQ_к = с_к · t_к · ΔG_п ; (4.14)

Если под потерями понимать теплоту, отдаваемую конденсатом через стенку корпуса аппарата, то по закону Фурье

Q = (λ_ст.к./ δ_ст.к.)·F_ст.к.·(t_к - t_нар.), (4.15)

где λ, δ и F есть коэффициент теплопроводности, толщина и площадь внутренней поверхности стенки корпуса аппарата, а t_нар. – температура окружающей среды. Поскольку все входящие в формулу величины являются либо константами (λ_ст.к, t_к) , либо фиксированы конструкцией аппарата (δ_ст.к, F_ст.к) и условиями эксплуатации (t_нар.), Q_пот не зависит от величин, включенных нами в рассмотрение. Это означает, что

ΔQ_пот = 0. (4.16)

Теперь все величины, входящие в уравнение в отклонениях, известны. Осталось подставить их в уравнение и выполнить некоторые простые преобразования.

0,5 V·ρ_в· c_в·Δt₂ = (i_п· ΔG_п + c_в · t₁₀ ·ΔG_в + 0,5α·F_т·Δt₂ - c_в · (t₂₀ –t₁₀) · ΔG_в –

- c_в· G_в0 · Δ t₂ - с_к · t_к · ΔG_п)· Δτ.

После группирования слагаемых относительно приращений рассматриваемых переменных (Δt₂, ΔG_п, ΔG_в), переноса выражения, содержащего управляемую переменную, в левую часть, деления обеих частей уравнения на Δτ и выполнения предельного перехода при Δτ → 0 получим уравнение динамики в виде

0,5 V·ρ_в· c_в· 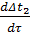+ (c_в· G_в0 - 0,5α·F_т) ·Δt₂ = (i_п - с_к · t_к) · ΔG_п +

+ c_в· (2 t₁₀ - t₂₀) · ΔG_в . (4.17)

Теперь введем обозначения:

0,5 V·ρ_в· c_в / (c_в· G_в0 - 0,5α·F_т) = T; (4.18)

(i_п - с_к · t_к) / (c_в· G_в0 - 0,5α·F_т) = К1; (4.19)

c_в· (2 t₁₀ - t₂₀) / (c_в· G_в0 - 0,5α·F_т) = К2, (4.20)

после чего уравнение динамики примет хорошо знакомый вид:

Т 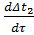+ Δt₂ = К1· ΔG_п + К2· ΔG_в . (4.21)

Теперь задача свелась к определению численных значений постоянной времени Т и коэффициентов К1 и К2. Чтобы убедиться в том, что Т – постоянная именно времени, достаточно проверить ее размерность

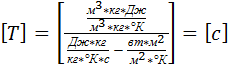, так как .

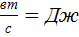Для определения значения Т кроме табличных значений ρ_в = 3175 кг/м³ и c_в = 4,2 кДж/(кг· 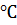) *⁾, регламентного значения расхода воды G_в0 , необходимо вычислить по конструктивным параметрам общую площадь F_т контакта пара с трубками и объем воды в трубках, а также коэффициент теплопередачи α при конденсации пара на вертикальных стенках трубок.

При расчете F_т закругления труб при смене направления хода воды заменим прямыми участками и будем считать длину трубок L = 2,6 м.

Тогда F_т = π·d_нар.· L·n (4.22)

F_т = 3,14·16·10^-3·2,6·256 = 33,44 м² .

Для вычисления α воспользуемся формулой (4.52) на стр. 161 в [ ]. Она как раз для случая конденсации водяного пара на пучке вертикальных труб: α = 2,04·7420 /( L·Δt)^1/4 . (4.23)

Здесь Δt определим как разницу между температурой наружного конденсата и средней температурой воды в трубках:

Δt = 143 – 0,5(20 + 150) = 58 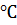. Тогда α = 2,04·7420 /( 2,6·58)^1/4 , что составляет 4319,86 Вт/ (м² ·◦К) или 4, 32 кДж/(м² ·◦К).

Внутренний объем труб считается легко:

V = π·d ²_вн.· L·n/4 (4.24) V = 3,14·14² ·10^-6 ·2,6·256/4 ≈ 0,1 м³ .

Определим значение постоянной времени по (4.18):

Т = 0,1·3175·4,2 / 2(4,2·20 – 0,5·4,32·33,44) = 1333,5 / 2·11,77 = 56,65 с.

При определении значения коэффициента К1 необходимо знать удельную энтальпию пара. Ее значение уже было найдено по таблице состояний воды и водяного пара [ ], а за значение теплоемкости конденсата (ведь это уже вода) возьмем известное значение для c_в . ____________

*⁾ Здесь используется значение теплоемкости воды при нормальных условиях. На самом деле оно несколько другое при повышенных давлении и температуре. Однако для учебных целей это не имеет решающего значения.

По формулам (4.19) и (4.20)

К1 = (2744 – 4,2·143) / (4,2·20 – 0,5·4,32·33,44) = 2143,4 / 11,77 = 182,107.

К2 = 4,2·(2·20 - 150) / (4,2·20 – 0,5·4,32·33,44) = -462 / 11,77 = - 39,25.

И уравнение динамики приобретает окончательный вид

56,65 · 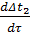Δt₂ = 182,107 · ΔG_п – 39,25 · ΔG_в. (4.25)

Теперь можно выписать полную математическую модель. Но для этого не хватает регламентного значения расхода пара. Для составления уравнения динамики значение G_п0 не потребовалось, но оно входит в уравнение статики. И расходуется подаваемый пар в том числе и на потери тепла. Сами потери были оценены как не зависящие от рассматриваемых нами величин в силу постоянства температуры конденсата. Но знать-то их надо. Поэтому в соответствии с законом Фурье (4.15)

Q_пот. = 17,5·0,82·π·2,6·(143 - 20) / 0,01 ≈ 1441 кДж. Такую теплоту содержат, в соответствии с (4.7) , G_пп = 1441 / 2744 = 0,525 кг пара /с.

Расход пара только на нагрев воды можно определить по формуле

G_пв = c_в · G_в ·(t₂₀ –t₁₀) / (i_п – i_к). (4.26)

Смысл ее прост: скрытая теплота парообразования, выделяющаяся при конденсации, расходуется на нагрев воды от температуры t₁₀ до t₂₀ .

G_пв = 4,2·20·130 / (2744 - 601) = 5,1 кг/с.

Общий расход пара , естественно, равен сумме

G_п0 = G_пп + G_пв. (4.27)

G_п0 = 5,625 кг /с.

Здесь уместно проверить с каким кпд работает аппарат. Ведь на практике он составляет не менее 0,9.

Кпд = 5,1 / 5,625 = 0,907. Отсюда можно заключить, что наши расчеты не противоречат существующей практике эксплуатации аппаратов подобного типа. Но вернемся к основной задаче: выписыванию математической модели в явном виде и построению структурной схемы системы управления технологическим объектом по его математической модели.

Полная математическая модель представлена на следующей странице.

Для построения структурной схемы системы управления по математической модели к обеим частям уравнения (4.25) применим преобразование Лапласа. Получим уравнение

56,65p· + = - .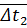

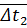
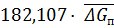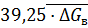Теперь передаточные функции по каналам управления и возмущения легко могут быть определены.

┌

│ Конструктивные параметры:

│ L = 2,6 м; d_тр = 16 х 1; D_вн.к. = 0,82 м; δ_ст.к. = 0,01 м;

│ V = const, F_тр = const.

│ Допущения:

│ ρ_в = const; c_в = const; G_к = G_п ; t_п = const и t₁ = const.

│ Использованные соотношения между рассматриваемыми

│ величинами:

│ (4.3) – (4.15), (4.22) - (4.24) , (4.26), (4.27).

│ Уравнение статики:

│ Q_в = Q_п + Q₁ – Q_т – Q₂ - Q_к - Q_пот

│ Уравнение динамики:

│ 0,5 V·ρ_в· c_в· 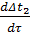+ (c_в· G_в0 - 0,5α·F_т) ·Δt₂ = (i_п - с_к · t_к) · ΔG_п +

│ + c_в· (2 t₁₀ - t₂₀) · ΔG_в .

│ Регламентный режим:

│( t₁₀= 20 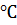, G_в0 = 20 кг/с, t₂₀= 150 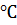, G_п0 = 5,625 кг /с, t_ос.0 = 20 )

└

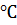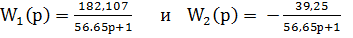
Структурная схема системы управления технологическим объектом по математической модели изображена на рис. 4.3.

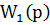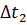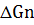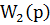Рис. 4.3. Структурная схема управления по мат. модели

ПРИЛОЖЕНИЕ 2

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Санкт-Петербургский государственный технологический университет растительных полимеров

Факультет автоматизированных систем управления технологическими процессами

Кафедра автоматизации технологических процессов

и производств