Основные этапы построения математической модели
методом«чёрного ящика»
1. Изучение системы; выделение входных и выходных
величин
Рассмотрим систему, связанную с окружающей средой посредством входных (неуправляемых и управляемых) и выходных параметров.
Из множества связей системы с окружающей средой, исходя из того, что известно об объекте, выбирают входные параметры хi. При проведении эксперимента измеряют значения выходных параметров yi (или одного параметра — критерия, который часто называют целевой функцией Y), также выбранных, исходя из целей исследования.
2. Задание структуры математической модели
На втором этапе постулируется вид математической связи (оператор связи) между входными и выходными величинами
с определением вида уравнения для описания зависимости.
В общем случае уравнение имеет вид
Y = f(хi, А), (14)
где А — параметры математической модели,
i = 1, …, k.
 |
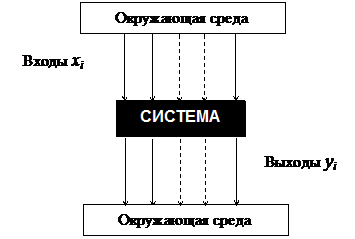Рис.6. Система как «чёрный ящик»
3. Нахождение параметров математической модели
После нахождения коэффициентов уравнения проводят статистический (регрессионный) анализ результатов.
Как правило, экспериментальные данные описывают уравнением регрессии, например, полиномом вида
y = a0 + a1x1 + a2х2+…. + aixi2. (15)
Линия, проходящая через средние значения выходной величины, называется регрессионной кривой или линией регрессии.
 |
Рис. 7. Построение линии регрессии
При нахождении коэффициентов уравнения регрессии, как правило, применяют метод наименьших квадратов. Коэффициенты подбирают таким образом, чтобы отклонение значений выходных(экспериментальных) величин (уi) и величин (ŷ), рассчитанных по уравнению регрессии, было минимальным.
4. Проверка адекватности математической модели
Адекватность — это соответствие данных, рассчитанных по математической модели, экспериментальным данным.
Адекватность уравнения проверяют по статистическому
критерию Фишера:
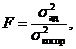(16)
где s2ад — дисперсия адекватности, s2воспр — дисперсия
воспроизводимости.
Дисперсия адекватности оценивает точность математической модели, а дисперсия воспроизводимости характеризует разброс выходных величин при одинаковых значениях входных, т. е. точность проведения эксперимента.
Для определения s2воспр обязательным условием является проведение параллельных опытов. Распределение Фишера характеризуется двумя параметрами — числами степеней сво-
боды:
f1 = fад = n – l, f2 = fвоспр = m – l,
где n – число коэффициентов в уравнении регрессии, m – число параллельных опытов.
Если F будет меньше табличного значения F1–p (f1, f2) для выбранного уровня значимости р, т. е. вероятности попадания
в критическую область (область маловероятных значений случайной величины) данного распределения для чисел степеней свободы f1 и f2, то уравнение адекватно эксперименту.
Величина р показывает, какова вероятность того, что модель может быть отнесена к разряду неадекватных, а величина 1 – р представляет собой вероятность, с которой уравнение можно считать адекватным эксперименту.
Если математическая модель неадекватна, то либо меняют её структуру, либо проводят дополнительные эксперименты (расширение базы экспериментальных данных).
5. Проверка значимости параметров математической модели.
Для проверки значимости параметров модели применяют критерий Стьюдента. При соответствующих степенях свободы
с помощью таблицы определяют критическое значение параметра и сопоставляют с известным значением. Параметр считается значимым, если его значение больше табличного или равно ему. Если один или несколько параметров незначимы, то их исключают из уравнения, и остальные параметры пересчитывают заново (переход к п. 3). Если все параметры значимы, то построение математической модели завершено.
В дальнейшем проводят адаптацию модели, т.е. подстройку её параметров с целью повышения адекватности.
Построение модели методом «чёрного ящика» применяют при анализе сложных систем, когда невозможно установить их внутренние связи. Понятие «чёрный ящик» помогает также при изучении поведения систем, т.е. их реакций на различные внешние воздействия, абстрагироваться от их внутреннего устройства. Многие системы, особенно большие, оказываются
настолько сложными, что, даже имея полную информацию о состоянии их элементов, практически невозможно связать её с поведением системы в целом. В подобных случаях представление такой сложной системы в виде некоторого «чёрного ящика», функционирующего аналогично, облегчает построение упрощенной модели. Анализируя поведение модели и сравнивая его с поведением системы, можно сделать ряд выводов о свойствах самой системы и при их совпадении со свойствами модели выбрать рабочую гипотезу о предполагаемом строении исследуемой системы.
Метод «чёрного ящика» также весьма полезен при замене одной системы другой, функционирующей аналогичным образом. Модель в виде «чёрного ящика» в ряде случаев оказывается единственно применимой при изучении некоторых систем. Это относится к таким исследованиям, в результате которых нужно получить данные о системе в обычной для неё обстановке.
К моделированию методом «чёрного ящика» относится и экспериментально-статистический метод построения математической модели. В основе данного метода лежит проведение большого числа экспериментов с последующей статистической обработкой их результатов. Достоинства метода: простота математической модели и процесса е ё получения, точность, универсальность метода построения. Недостатки: математическая модель применима только для той системы, на которой проводился эксперимент, и ограниченная область варьирования параметров.
Экспериментально-статистические методы построения математических моделей подразделяют как по виду моделей (динамические и статические), так и по способу сбора экспериментальных данных (на основе пассивного или активного эксперимента).
В активном эксперименте одновременно варьируются все факторы, как правило, на двух уровнях (верхнем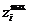 
и нижнем 
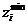) относительно некоторого уровня 
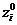, называемого основным или нулевым. Интервал варьирования определяют по выражению
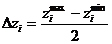. (17)
При переходе к безразмерной системе координат проводим следующее преобразование:
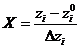. (18)
Обозначения уровней:
+1 — основной, 0 — нулевой, –1 — нижний.
Критические значения критериев Стьюдента и Фишера представлены в приложениях 1, 2.
ЗАДАНИЕ
Известно, что на эффективность обезвреживания нефте-содержащих отходов влияют три основных фактора. Необходимо определить коэффициенты уравнения регрессии и оценить степень влияния факторов на целевую функцию. Матрица планирования приведена в табл.3, а экспериментальные дан-
ные — в табл.4. В каждом эксперименте проведено три параллельных опыта.
Таблица 3
Матрица планирования
| Номер опыта | Х0 | Х1 | Х2 | Х3 | Х1Х2 | Х1Х3 | Х2Х3 | Х1Х2Х3 |
| +1 +1 +1 +1 +1 +1 +1 +1 | +1 –1 +1 –1 +1 –1 +1 –1 | +1 +1 –1 –1 +1 +1 –1 –1 | +1 +1 +1 +1 –1 –1 –1 –1 | +1 –1 –1 +1 +1 –1 –1 +1 | +1 –1 +1 –1 –1 +1 –1 +1 | +1 +1 –1 –1 –1 –1 +1 +1 | +1 –1 –1 +1 –1 +1 +1 –1 |
РЕШЕНИЕ
1. Вычислим среднее значение параметра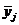 
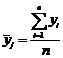
и дисперсию опыта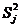 
,
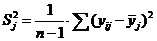де n — число параллельных опытов.
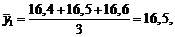Для некоторого опыта под номером 1 в серии из 8 опытов
получим
 |
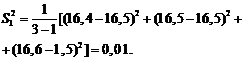Таблица 4
Полученные результаты
| Номер опыта | у1i | у2i | у3i |  | S2j | ŷ |
| ∑ | 16,40 4,30 20,40 12,50 19,30 7,40 23,30 15,30 | 16,50 4,40 20,50 12,60 19,50 7,60 23,40 15,50 | 16,60 4,60 20,60 12,70 19,70 7,70 23,50 15,70 | 16,50 4,43 20,50 12,60 10,50 7,56 23,40 15,50 | 0,01 0,023 0,01 0,01 0,04 0,023 0,01 0,04 0,166 | 16,50 4,50 20,45 12,50 19,49 7,49 23,44 15,54 |
2. Определим принадлежность рассчитанных дисперсий одной генеральной совокупности, для чего найдем значение критерия Кохрена G и сравним его с табличным, определенным для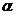 
=0,05, N =8, f = 2, где N – число опытов.
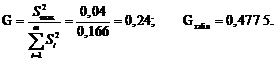
3. Определим дисперсию воспроизводимости
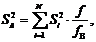
где f = (n – 1)=2, fВ = N (n – 1) = 16.
4. Вычислим коэффициенты уравнения по следующей
формуле:
.
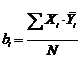Например,
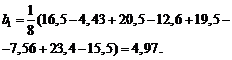
Аналогично вычислим коэффициенты b0 (15,00), b2 (–3,00), b3 (–1,49), b12 (1,07), b13 (0,016), b23 (0,041), b123 (0,016 6)
и определим их значимость по критерию Стьюдента (t). Коэффициенты значимы, если выполняется условие:
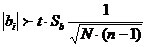, tтабл = 2,12, для fB = 16.
После исключения из уравнения незначимых коэффициентов получим следующее уравнение
Y = 15,00 + 4,97 X1 – 3,00 X2 – 1,49 X3 + 1.07 X12.
Положительный (отрицательный) знак коэффициента означает, что при возрастании данного параметра увеличивается (уменьшается) и целевая функция.
Рассчитываем значения ŷ и вносим их в табл.4.
Определяем дисперсию адекватности
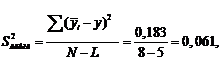
где L — число значимых коэффициентов в уравнении регрессии.
Находим значение критерия Фишера
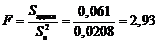
и сравниваем его с табличным (приложение 1), определенным при f2* = 16 и числе степеней свободы, равном 3.
Если F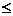 
Fтабл (как в данном примере), то уравнение адекватно описывает эксперимент.
Следует отметить, что все вычисленные коэффициенты уравнения были определены при условии первоначального их выражения в кодированной (безразмерной) форме и для того, чтобы получить с помощью уравнения значения целевой функции в натуральных единицах измерения, необходимо использовать
натуральный масштаб.
Варианты исходных данных к заданиям
| Значе- ния Y1, 2, 3 | Номер опыта | ||||||||
| I | Y1 | 18,2 | 14,6 | 17,4 | 4,3 | 7,8 | 3,2 | 11,5 | 2,8 |
| Y2 | 18,4 | 14,0 | 17,2 | 4,2 | 7,9 | 3,0 | 11,4 | 2,9 | |
| Y3 | 18,1 | 13,1 | 17,0 | 4,1 | 8,5 | 3,8 | 11,2 | 2,8 | |
| II | Y1 | 14,2 | 12,7 | 15,3 | 11,5 | 2,2 | 17,4 | 14,7 | 3,6 |
| Y2 | 14,6 | 12,1 | 15,8 | 11,4 | 2,3 | 17,2 | 15,2 | 3,5 | |
| Y3 | 14,0 | 11,8 | 15,9 | 11,2 | 2,5 | 17,0 | 14,8 | 3,9 | |
| III | Y1 | 13,1 | 15,4 | 14,5 | 14,7 | 1,8 | 15,3 | 12,3 | 18,0 |
| Y2 | 12,7 | 16,5 | 15,9 | 15,2 | 1,9 | 15,8 | 12,4 | 17,4 | |
| Y3 | 12,2 | 16,5 | 15,2 | 16,0 | 1,7 | 15,9 | 12,8 | 17,2 | |
| IV | Y1 | 9,6 | 17,2 | 14,6 | 12,3 | 3,6 | 14,5 | 12,8 | 15,2 |
| Y2 | 9,4 | 17,5 | 14,0 | 12,4 | 3,5 | 15,9 | 12,9 | 15,3 | |
| Y3 | 9,0 | 17,8 | 13,1 | 12,8 | 3,0 | 15,2 | 12,0 | 15,8 | |
| V | Y1 | 17,4 | 12,3 | 12,7 | 12,8 | 2,5 | 14,6 | 11,4 | 15,9 |
| Y2 | 17,2 | 12,1 | 12,1 | 12,9 | 2,2 | 14,0 | 11,5 | 14,5 | |
| Y3 | 17,0 | 12,0 | 11,8 | 2,0 | 13,1 | 11,9 | 15,9 | ||
| VI | Y1 | 15,3 | 11,5 | 15,4 | 11,4 | 4,2 | 12,7 | 8,5 | 15,2 |
| Y2 | 15,8 | 11,4 | 16,5 | 11,5 | 4,5 | 12,1 | 8,6 | 14,6 | |
| Y3 | 15,9 | 11,2 | 16,5 | 11,9 | 4,8 | 11,8 | \8,0 | 14,0 | |
| VII | Y1 | 14,5 | 14,7 | 17,2 | 2,3 | 5,6 | 15,4 | 7,4 | 13,1 |
| Y2 | 15,9 | 15,2 | 17,5 | 2,5 | 5,8 | 16,5 | 7,1 | 12,7 | |
| Y3 | 15,2 | 16,0 | 17,8 | 3,2 | 5,4 | 16,5 | 7,0 | 12,1 | |
| VIII | Y1 | 14,6 | 12,3 | 12,3 | 3,1 | 8,1 | 17,2 | 11,5 | 15,8 |
| Y2 | 14,0 | 12,4 | 12,1 | 3,3 | 8,2 | 17,5 | 11,4 | 15,4 | |
| Y3 | 13,1 | 12,8 | 12,0 | 2,2 | 17,8 | 11,2 | 16,5 | ||
| IX | Y1 | 12,7 | 12,8 | 3,6 | 2,3 | 17,4 | 12,3 | 14,7 | 16,5 |
| Y2 | 12,1 | 12,9 | 3,5 | 2,8 | 17,2 | 12,1 | 15,2 | 17,2 | |
| Y3 | 11,8 | 12,0 | 3,0 | 3,1 | 17,0 | 12,0 | 16,0 | 17,5 | |
| X | Y1 | 15,4 | 11,4 | 2,4 | 2,6 | 15,3 | 3,2 | 12,3 | 12,8 |
| Y2 | 16,5 | 11,5 | 2,8 | 2,5 | 15,8 | 3,1 | 12,4 | 12,3 | |
| Y3 | 16,5 | 11,9 | 2,9 | 2,8 | 15,9 | 3,3 | 12,8 | 12,1 | |
| ХI | Y1 | 17,2 | 18,3 | 3,2 | 17,4 | 14,5 | 2,2 | 12,8 | 2,8 |
| Y2 | 17,5 | 18,4 | 3,1 | 17,2 | 15,9 | 2,3 | 12,9 | 3,2 | |
| Y3 | 17,8 | 18,0 | 3,3 | 17,0 | 15,2 | 2,8 | 3,1 | ||
 | |||||||||
 | |||||||||
| Значе- ния Y1, 2, 3 | Номер опыта | ||||||||
| ХII | Y1 | 12,3 | 17,5 | 2,2 | 15,3 | 14,6 | 3,1 | 11,4 | 3,3 |
| Y2 | 12,1 | 17,1 | 2,3 | 15,8 | 14,0 | 2,6 | 11,5 | 2,2 | |
| Y3 | 12,0 | 17,0 | 2,8 | 15,9 | 13,1 | 2,5 | 11,9 | 2,3 | |
| ХIII | Y1 | 11,5 | 12,3 | 3,1 | 14,5 | 12,7 | 17,4 | 14,3 | 2,8 |
| Y2 | 11,4 | 12,5 | 2,6 | 15,9 | 12,1 | 17,2 | 14,5 | 3,1 | |
| Y3 | 11,2 | 12,4 | 2,5 | 15,2 | 11,8 | 17,0 | 14,0 | 2,6 | |
| ХIV | Y1 | 14,7 | 3,2 | 1,8 | 14,6 | 15,4 | 15,3 | 7,8 | 2,5 |
| Y2 | 15,2 | 3,1 | 1,9 | 14,0 | 16,5 | 15,8 | 7,9 | 3,2 | |
| Y3 | 16,0 | 3,3 | 2,2 | 13,1 | 16,5 | 15,9 | 7,8 | 3,1 | |
| ХV | Y1 | 12,3 | 2,2 | 11,5 | 12,7 | 17,2 | 14,5 | 11,5 | 3,3 |
| Y2 | 12,4 | 2,3 | 11,4 | 12,1 | 17,5 | 15,9 | 11,4 | 2,2 | |
| Y3 | 12,8 | 2,8 | 11,2 | 11,8 | 17,8 | 15,2 | 11,2 | 2,3 | |
| ХVI | Y1 | 12,8 | 3,1 | 14,7 | 15,4 | 12,3 | 14,6 | 14,7 | 2,8 |
| Y2 | 12,9 | 2,6 | 15,2 | 16,5 | 12,1 | 14,0 | 15,2 | 3,1 | |
| Y3 | 2,5 | 16,0 | 16,5 | 12,0 | 13,1 | 16,0 | 2,6 | ||
| ХVII | Y1 | 11,4 | 3,2 | 12,3 | 17,2 | 3,2 | 12,7 | 12,3 | 2,5 |
| Y2 | 11,5 | 3,1 | 12,4 | 17,5 | 3,1 | 12,1 | 12,4 | 3,2 | |
| Y3 | 11,9 | 3,3 | 12,8 | 17,8 | 3,3 | 11,8 | 12,8 | 3,1 | |
| ХVIII | Y1 | 18,3 | 2,2 | 12,8 | 12,3 | 2,2 | 15,4 | 12,8 | 3,3 |
| Y2 | 18,4 | 2,3 | 12,9 | 12,1 | 2,3 | 16,5 | 12,9 | 2,2 | |
| Y3 | 18,0 | 2,8 | 12,0 | 2,8 | 16,5 | 2,3 | |||
| ХIX | Y1 | 17,5 | 3,1 | 11,4 | 11,4 | 3,1 | 17,2 | 11,4 | 2,8 |
| Y2 | 17,1 | 2,6 | 11,5 | 11,5 | 2,6 | 17,5 | 11,5 | 3,1 | |
| Y3 | 17,0 | 2,5 | 11,9 | 11,0 | 2,5 | 17,8 | 11,9 | 2,6 | |
| ХX | Y1 | 12,3 | 2,9 | 8,5 | 10,8 | 3,2 | 12,3 | 8,9 | 2,5 |
| Y2 | 12,5 | 3,2 | 8,6 | 10,5 | 2,5 | 12,1 | 7,4 | 2,5 | |
| Y3 | 12,4 | 3,3 | 8,2 | 10,4 | 2,8 | 12,0 | 7,2 | 2,1 |
Библиографический список
1. Кафаров В.В. Методы кибернетики в химии и химической технологии. — М.: Химия, 1976. —464с.
2. Бондарь А.Г. Математическое моделирование в химической технологии. — Киев: Вища школа, 1973. —280 с.
Значения критерия Фишера
| f2* | Число степеней свободы | |||||
| 161,4 | 199,5 | 215,7 | 224,6 | 230,2 | 234,0 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | |
| 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | |
| 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | |
| ∞ | 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 |
*f2 — число степеней свободы для меньшей дисперсии
ПРИЛОЖЕНИЕ 1
для уровня значимости α = 0,05
| f1 для большей дисперсии | ||||||
| ∞ | ||||||
| 238,9 | 243,9 | 246,5 | 249,0 | 251,8 | 253,3 | 254,0 |
| 19,37 | 19,41 | 19,43 | 19,45 | 19,47 | 19,49 | 19,50 |
| 8,84 | 8,74 | 8,69 | 8,64 | 8,58 | 8,56 | 8,53 |
| 6,04 | 5,91 | 5,84 | 5,77 | 5,70 | 5,66 | 5,63 |
| 4,82 | 4,68 | 4,60 | 4,53 | 4,44 | 4,40 | 4,36 |
| 4,15 | 4,00 | 3,92 | 3,84 | 3,75 | 3,71 | 3,67 |
| 3,73 | 3,57 | 3,49 | 3,41 | 3,32 | 3,28 | 3,23 |
| 3,44 | 3,28 | 3,20 | 3,12 | 3,03 | 2,98 | 2,93 |
| 3,23 | 3,07 | 2,98 | 2,90 | 2,80 | 2,76 | 2,71 |
| 3,07 | 2,91 | 2,82 | 2,74 | 2,64 | 2,59 | 2,54 |
| 2,95 | 2,79 | 2,70 | 2,61 | 2,50 | 2,45 | 2,40 |
| 2,85 | 2,69 | 2,60 | 2,50 | 2,40 | 2,35 | 2,30 |
| 2,77 | 2,60 | 2,51 | 2,42 | 2,32 | 2,26 | 2,21 |
| 2,70 | 2,53 | 2,44 | 2,35 | 2,24 | 2,19 | 2,13 |
| 2,64 | 2,48 | 2,39 | 2,29 | 2,18 | 2,12 | 2,07 |
| 2,59 | 2,42 | 2,33 | 2,24 | 2,13 | 2,07 | 2,01 |
| 2,45 | 2,28 | 2,28 | 2,08 | 1,96 | 1,90 | 1,84 |
| 2,27 | 2,09 | 1,99 | 1,89 | 1,76 | 1,69 | 1,62 |
| 2,18 | 2,00 | 1,90 | 1,79 | 1,66 | 1,59 | 1,51 |
| 2,13 | 1,95 | 1,85 | 1,74 | 1,60 | 1,52 | 1,44 |
| 2,03 | 1,85 | 1,75 | 1,63 | 1,48 | 1,39 | 1,28 |
| 1,94 | 1,75 | 1,64 | 1,52 | 1,35 | 1,24 | 1,00 |
Содержание
Теория подобия и π-теорема........................................... 3
Варианты заданий.......................................................... 12
Практическое применение метода
линейного программирования...................................... 14
Варианты заданий.......................................................... 20
Матричное представление
структуры химико-технологических систем............... 25
Варианты заданий.......................................................... 30
Моделирование методом «чёрного ящика»................. 31
Варианты исходных данных к заданиям...................... 41
Приложения............................................................ 45
Учебное издание
Суфиянов Ракип Шайхиевич
Горбенко Ольга Олеговна
ЭЛЕМЕНТЫ СИСТЕМНОГО АНАЛИЗА
Компьютерная вёрстка: А.Г. Ланцетти
Подписано в печать 12.01.09. Форм.бум. 60´84 1/16.
Усл. печ. л. 3,2. Уч.-изд. л. 3,25. Тираж 150 экз.
МГУИЭ, издательский центр
105066, Москва, ул. Старая Басманная, 24/1