Раздел II ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Высшая математика: Методические рекомендации по выполнению домашней контрольной работы / М.А.Сагадеева - Челябинск: ЧОУ ВПО «Южно-Уральский институт управления и экономики», 2012.- 23 с.

Высшая математика:Методические рекомендации по выполнению домашней контрольной работы: 140400.62 «Электроэнергетика и электротехника»

ã Издательство ЧОУ ВПО «Южно-Уральский институт управления и экономики», 2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 4

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ.. 5

ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ.. 13

РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ.. 20

ВВЕДЕНИЕ

Цель курса Высшая математика в системе подготовки – освоение необходимого математического аппарата.

Задачи изучения Высшей математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке навыков решения основных задач Высшей математики, что в конечном итоге формирует навык исследования моделей реальных процессов.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ

Раздел I СХОДИМОСТЬ НЕСОБСТВЕННЫХ
ИНТЕГРАЛОВ И ЧИСЛОВЫХ РЯДОВ

Тема 1 Несобственный интеграл

Вычисляется как интеграл с одним или с двумя неограниченными пределами. Подынтегральная функция определена и непрерывна на одном из промежутков [a;+¥), (-¥;b], [-¥;+¥].

Если несобственный интеграл сходится, то он имеет конечный предел, если не сходится, то предел его равен бесконечности (2, с.271, 272).

Для вычисления площадей плоских фигур необходимо уметь определять пределы интегрирования, если они не заданы и если площадь фигуры представляется в виде сумм или разностей криволинейных трапеций. Поэтому нужно построить кривые, ограничивающие плоские фигуры, определяют граничные условия (пределы интегрирования). Необходимо разобрать примеры (1,11.5–11.7, 11.20–11.22, с.300–304, 313), (2, с.261, примеры 11.30–11.35).

Формула трапеций применяется для приближенного вычисления определенного интеграла, когда соответствующая первообразная не вычисляется непосредственным интегрированием.

Разобрать примеры по теме (1, N 11.1–11.11, 11.18–11.22, задачи для самостоятельной работы N 11.25–11.30,11.32–11.35,11.37–11.39, 11.41, 11.42, 11.43–11.52, 11.57, 11.59), (2,11.1 а), б), в), г), д), е), 11.30–11.35, задачи для самостоятельной работы 11.2–11.28, 11.36–11.53, 11.54–11.57, 11.58–11.61, 11.62–11.71, 11.75–11.86).

Тема 2 Числовые ряды

Студенту при изучении темы нужно усвоить определение:

а) числового ряда;

б) определение сходящегося ряда.

Изучив свойства рядов и при этом разобраться в том, что необходимый признак сходимости (для сходящихся рядов U_n®0 при n®¥) не является достаточным.

Необходимо использовать в качестве эталонных расходящихся рядов гармонический ряд и ряд вида 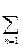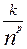при p=1, k>0; для сходящихся рядов в качестве эталонных использовать геометрический ряд 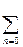aqⁿ при ½q½<1 и ряды вида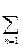 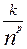при p>1, k>0.

Студенту нужно усвоить тот факт, что признаки сравнения применяют тогда, когда признаки Даламбера и Коши не дают результата.

Исследование сходимости знакочередующегося ряда с использованием признака Лейбница.

Раздел II ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Тема 3 Степенные ряды

Главным вопросом при изучении этой темы является вопрос определения радиуса сходимости степенного ряда.

В промежутке (-R;R) степенной ряд сходится абсолютно для любых х. Важно исследовать сходимость числовых рядов на границах интервала. Для знакочередующегося ряда для этой цели необходимо использовать признаки сравнения или признак Лейбница, признак Даламбера применять нецелесообразно.

Ряд Маклорена может сходиться к конкретной функции только в некотором промежутке (определяется интервал его сходимости), может вообще расходиться или сходиться к другой функции.

Пример решения задачи по теме «Ряды».

Прежде всего отметим, что областью сходимости называется совокупность тех значений, при которых степенной ряд сходится.

Дан ряд .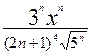

Алгоритм решения.

1) Находим радиус сходимости ряда

R= 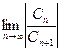=lim =

= = .

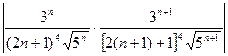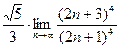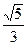2) необходимо выяснить поведение ряда на концах отрезка, выяснить сходимость ряда.

На первом конце х= – 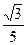ряд принимает вид

1– 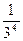+ +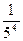…+ 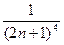– знакопеременный ряд.

Применяем для исследования этого ряда признак Лейбница (3, с.369).

n=2m.

Отметим:

а) что члены знакочередующегося ряда убывают по абсолютной величине

1> > >…> .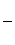

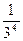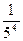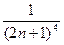б) пределы общего члена

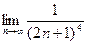=0.

По признаку Лейбница ряд сходится.

На правом конце при х= 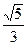ряд знакоположительный

1+ + +…+ .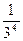

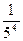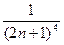Его можно сравнить с эталонным – обобщенным гармоническим рядом (применяется признак 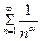, который сходится пр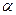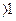и или 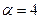в приведенном примере).

Вывод. Ряд сходится на обоих концах интервала.

Задача решена. Определен радиус сходимости ряда и исследована сходимость на границах интервала.

Тема 4 Ряды Фурье

Тригонометрическим рядом Фурье функции 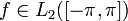называют функциональный ряд вида

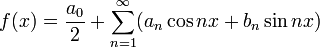(2)

где

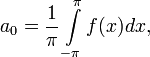
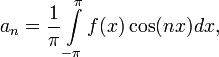
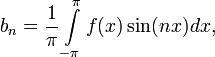
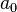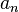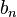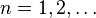Числа , и ( ) называются коэффициентами Фурье функции 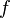. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию 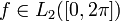в виде ряда (2), и нам надо определить неизвестные коэффициенты 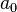, 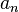и 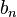. Если умножить правую часть (2) на 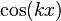и проинтегрировать по промежутку 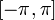, благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент 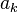. Аналогично для .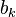