Построение графика функций одной переменной

В режиме непосредственных вычислений возможно построение графиков различных функций. Графики строятся в отдельных масштабируемых и перемещаемых окнах.

Пример — построение графика синусоиды. MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками. Зададим интервал изменения аргумента xот 0 до 10 с шагом 0.1. Для построения графика вначале зададим вектор аргумента: х=0:0.1:10. Затем используем команду построения графиков: plot(sin(x)). Результат показан на рис. 2.

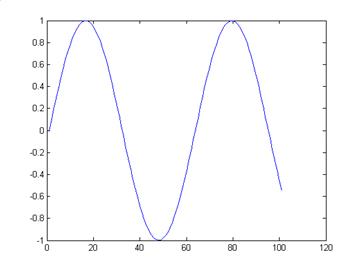
Рис. 1Пример построения графика синусоиды

Функция plot строит не истинный график функции sin(x), а заданное количеством элементов вектора х число точек. Эти точки затем соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. Для того, чтобы график был плавным, и не было заметно огранки вектор аргумента должен содержать достаточное количество точек.

Графики MATLAB строит в отдельных окнах, называемых графическими. В главном меню окна имеется позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис.2. Средства этой панели позволяют управлять параметрами графиков и наносить на них текстовые комментарии в любом месте. Для сравнения и анализа функций, удобно расположить несколько графиков одного аргумента расположить в одном окне. Это предусмотрено в MATLAB. Построим и сравним графики сразу трёх функций:

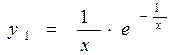
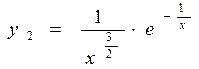
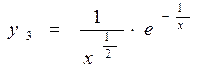
Для этого зададим общий для всех функций вектор аргумента:

>> x=[0.001:0.001:10];

Затем вычислим значения функций:

>> y1=(1./x).^0.5.*exp(-1./x);

>> y2=1./x.*exp(-1./x);

>> y3=(1./x).^1.5.*exp(-1./x);

Для построения графиков указанных функций в одном окне запишем следующее:

>> plot(x,y1,x,y2,x,y3); grid on

Результат поясняет рис. 3.

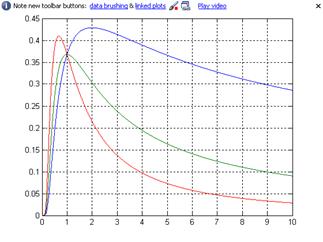
Рис. 2. Построение графиков трёх функций в одном окне

Оператор grid on включает изображение сетки. Аналогичный результат может быть получен удобнее. Для этого сначала нужно создать матрицу результатов вычисления значений функций, причём векторы y1, y2 и y3 должны быть столбцами (отделены при записи с помощью знака « ;» ):

>> Y=[y1;y2;y3];

а затем выполнить:

>> plot(x,Y) Так как MatLab автоматически масштабирует графики, для более подробного сравнения графиков функций можно задать границы просмотра, например:

>> a=100;b=1200;

>> Y=[y1(a:b);y2(a:b);y3(a:b)];

>> plot(x(a:b),Y); grid on

Здесь «а» и «в» – номера, соответственно, первого и последнего элементов массивов данных, используемых для построения графиков. Результат показан на рис.4., функции изображены на интервале (a:b) аргумента x.

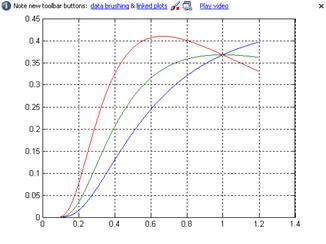
Рис. 3. Графики начальных участков трёх функций в одном окне