Тема 3.2. Частные производные
Частной производной по x функцииz = f(x,y) в точкеM0(x0,y0)называется предел

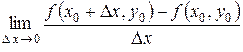 ,
,
если этот предел существует. Обозначается эта частная производная любым из следующих символов:
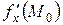 ;
; 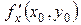 ;
; 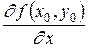 .
.
Частная производная по x есть обычная производная от функции z = f(x,y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функцииz = f(x,y) в точкеM0(x0,y0):
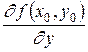 =
= 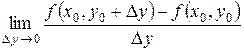 .
.
 |
В пространстве XYZ условие y = y0 описывает плоскость P, перпендикулярную оси OY и пересекающую эту ось в точке y0. Плоскость P пересекается с графиком функции z = f(x,y), вдоль некоторой линии L, как показано на рисунке 1. Тангенс угла между плоскостью XOY и касательной к линии L в точке с координатами x0,y0 равен частной производной по x функции z = f(x,y)в этой точке. В этом состоит геометрический смысл частной производной.
Аналогичное заключение можно сделать относительно частной производной по y.
Приведем примеры вычисления частных производных. Как говорилось выше, для вычисления частной производной по x функции z = f(x,y) нужно положить переменную y равной константе, а при нахождении частной производной по y нужно считать константой переменную x.
Примеры. 1. 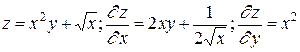 .
.
2. 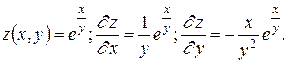
Если частные производные функции z = f(x,y) существуют на некотором множестве, а точка, в которой вычисляются частные производные несущественна, то пользуются более короткими обозначениями:
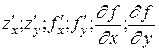 .
.
Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называютсявторыми частными производными или частными производными второго порядка и обозначаются zxx¢¢, zyy¢¢, zxy¢¢ или 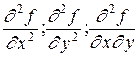 . Согласно определению
. Согласно определению 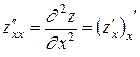 ;
; 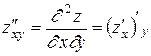 . Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная zxy¢¢ = (zx¢ )y¢ может не быть равной zyx¢¢ = (zy¢ )x¢. Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y. (Рекомендуем читателю самому убедиться в справедливости этой теоремы для функций, рассмотренных в приведенных выше примерах 1 и 2.)
. Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная zxy¢¢ = (zx¢ )y¢ может не быть равной zyx¢¢ = (zy¢ )x¢. Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y. (Рекомендуем читателю самому убедиться в справедливости этой теоремы для функций, рассмотренных в приведенных выше примерах 1 и 2.)
Отметим очень важное отличие функции двух переменных от функции одной переменной. Из существования первых частных производных в точке не следует непрерывность функции в этой точке. Рассмотрим, например, функцию
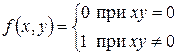 .
.
График этой функции во всех точках, не принадлежащих осям координат OX и OY, представляет собой плоскость, параллельную плоскости XOY, поднятую на 1. Сами эти оси координат также принадлежат графику рассматриваемой функции. Очевидно, что в точке (0,0) функция имеет частные производные по обоим аргументам, обе равные нулю. Очевидно также, что в любой окрестности точки (0,0) можно найти точку M такую, что f(M) = 1, в то время как f(0, 0) = 0. Это означает существование разрыва функции в точке (0,0). (Пример взят из книги О.С.Ивашева-Мусатова “Начала математического анализа”).
