Тема 3.3. Дифференциал функции двух переменных

Рассмотрим функцию z = f(x,y), имеющую в точке Р₀(х₀,у₀) частные производные f¢_x(х₀,у₀) и f¢_у(х₀,у₀). Перейдём от точки Р₀ к точке R₀(x₀+Dx,y₀+Dу), придавая переменным х и у в точке Р₀ произвольные приращения Dx и Dу, соответственно. При этом функция в точке Р₀ получит приращение

Df(х₀,у₀) = f(x₀+Dx,y₀+Dy) – f(x₀,y₀) = f(R₀) – f(P₀).

Если приращение функции f(x,y) можно представить в виде

Df(х₀,у₀) = f¢_x(х₀,у₀)Dx + f¢_у(х₀,у₀)Dу + a(Dx;Dу) Dx + b(Dx;Dу)Dу, (3.3.1)

где 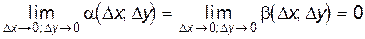, то функция называется дифференцируемойв точке Р₀(х₀,у₀). Сумма первых двух слагаемых в правой части равенства (1) называется дифференциалом функции f(x,y) в точке Р₀ и обозначается df(x₀,y₀):

df(x₀,y₀) = f¢_x(х₀,у₀)Dx + f¢_у(х₀,у₀)Dу. (3.3.2)

Если точка, в которой вычисляется дифференциал не существенна, его принято обозначать просто df. Из определения следует, что дифференциал представляет собой главную часть приращения функции, линейную относительно приращений её аргументов. Полагаяпоочерёдно f(x,y) = х и f(x,y) = у, получим, что дифференциалы dх и dy независимых аргументов функции х и у равны соответственно Dx и Dу . Таким образом

df = f¢_x dх + f¢_у dу.

Раньше говорилось о том, что из существования частных производных в точке не следует непрерывности функции в этой точке. Однако, из справедливости равенства (1) следует

,

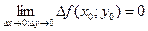а это означает непрерывность функции в точке (х₀,у₀). Следовательно, дифференцируемая в точке функция обязательно непрерывна в этой точке. Из сказанного следует, что существование обеих частных производных функции в точке не означает, что функция дифферен­цируема в этой точке. В курсе математического анализа доказывается теорема, что функция дифференцируема в точке, если обе частные производные этой функции непрерывны в этой точке.

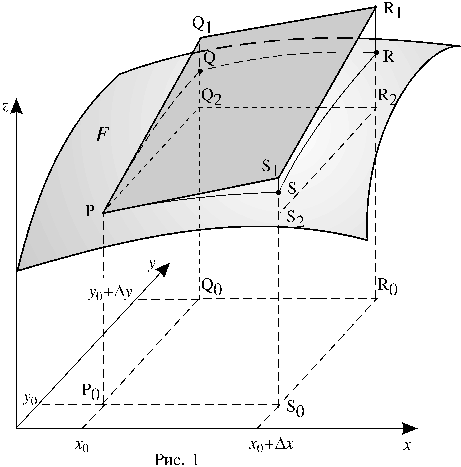На рисунке 1 график функции z = f(x,y) представляет собой поверхность F. Длина отрезка Р₀Р равна значению функции z в точке P₀, то есть çР₀Рç = f(x₀,y₀) (на рисунке для наглядности поверхность F выбрана так, что все рассматриваемые значения функции и приращения в точке P₀ положительны, но это не ограничивает справедливости приведенных выше выводов и формул в общем случае). Координатами точек Q₀, S₀ и R₀ являются пары чисел соответственно (x₀,y₀+Dу); (x₀+Dx,y₀) и (x₀+Dx,y₀+Dу), причём çQ₀Qç = f(Q₀), çS₀Sç = f(S₀) и çR₀Rç = f(R₀). Приращение Df(х₀,у₀) функции в точке Р₀ равно çRR₂ç.

Параллелограмм PQ₁R₁S₁ лежит в плоскости, которая касается поверхности F в точке Р. Прямоугольник PQ₂R₂S₂ расположен в горизонтальной плоскости. Очевидно: çQ₂Q₁ç = f¢_y(x₀,y₀)Dy и çS₂S₁ç = f¢_x(x₀,y₀)Dx.

Из легко доказываемого равенства

çR₂R₁ç = çS₂S₁ç + çQ₂Q₁ç

и формулы (2) следует, что дифференциал функции в точке Р₀ равен çR₂R₁ç.

Так как df(x₀,y₀) »Df(x₀,y₀), дифференциал df даёт приближенное значение приращения функции при малых значениях приращений аргументов.