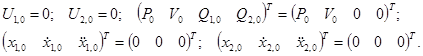Математическая модель ЗД

С.М. АЛФЁРОВ, А.М. КОРИКОВ

Моделирование задатчика давления для настройки манометров

Разработано математическое описание процессов, протекающих в задатчике давления (ЗД) автоматизированного стенда для настройки манометров, обоснована линеаризация уравнений, описывающих эти процессы, и получено их решение. На этой основе проведено моделирование ЗД, выполнено также сравнение модельных расчетов с экспериментальными данными.

Ключевые слова: автоматизация, манометр, автоматизированный стенд, задатчик давления, математическая модель, линеаризация, моделирование.

Введение

Манометрические приборы имеют разнообразные сферы применения: промышленность, транспорт, бытовая техника, научные исследования и т.д. Конкуренция производителей в данной области приборостроения высока и заставляет предприятия развиваться в направлении повышения качества выпускаемой продукции, осваивать новые технологии и осуществлять автоматизацию выпуска манометров [1,2]. В этом направлении проделан большой объем исследований, отраженный частично в цитируемых работах [1-4]. В [1] предложен проект системы автоматизированной настройки манометров с помощью нанесения шкал. В [3] предложены конструкция прибора, позволяющая автоматизировать процесс сборки манометра, способ автоматизированной сборки и расчет регулировочных параметров. В [4] разработан стенд для автоматизированной регулировки узлов манометров с трубкой Бурдона по одному параметру путем измерения характеристик чувствительного элемента и обработки механизма по вычисленному регулировочному параметру (координаты крепежного отверстия к чувствительному элементу). Поиск оригинальных технических решений проблемы автоматизации сборки и настройки манометров продолжается и, в частности соавтором данной статьи Алфёровым С.М. совместно с сотрудниками ОАО «Манотомь» разработан способиндивидуальной градуировки шкал манометров и устройство для его осуществления [2]. В проблеме автоматизации регулировки узлов манометров «узким» местом остается проблема автоматизации процесса управления давлением на стендовых манометрах. Успешное решение обозначенной актуальной задачи возможно с привлечением методов математического моделирования ЗД для настройки манометров. Именно этот путь реализуется в данной статье.

Постановка задачи

Важнейшей компонентой стенда для автоматизированной регулировки узлов манометров с трубкой Бурдона является гидравлическая установка, представленная на рис. 1. На этом рисунке использованы следующие обозначения: ДД – датчик давления (цифровой образцовый манометр), Ст – насосная станция, Вн₁, Вн₂ – вентили, Др – дроссель для настройки входного давления, Кл₁, Кл₂ – электромагнитные клапаны для подъема и сброса давления, УУ – устройство управления. Гидравлическая установка предназначена для плавной подачи и сброса давления на регулируемые манометры. Поясним кратко функциональное назначение основных компонент гидравлической установки с помощью рис. 1. Станция нагнетания давления Ст способна выдавать постоянное давление масла. Через вентиль Вн₁ давление масла подается на дроссель Др, с помощью которого можно настроить необходимое давление на вентиле Вн₂ и входе клапана Кл₁ (если Вн₂ открыт). Электромагнитные клапаны Кл₁ и Кл₂ способны плавно менять свою гидравлическую проводимость под действием напряжений U₁ и U₂, таким образом регулируются потоки масла Q₁ и Q₂ через клапаны и давление на манометрах P.

Определим суть процессов, протекающих в гидравлической установке с позиции теории управления. Выделим на схеме этой установки объект управления (ОУ). Тогда данная схема может быть представлена в виде рис. 2, на котором в качестве ОУ представлен ЗД (на рис. 1 ему соответствует система клапанов Кл₁ и Кл₂, выделенная пунктиром). Управлению клапанами мешают эффекты «залипания» задвижки клапана, которые, возможно, объясняются силами сухого трения. Для успешного управления давлением требуется построить математическую модель ЗД. Управляемым параметром является давление P. Управляющие параметры: U₁ и U₂.

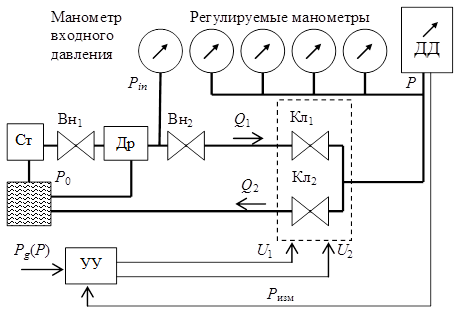
Рис. 1. Схема гидравлической установки

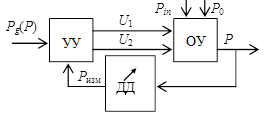
ОУ – объект управления.

Рис. 2. Структурная схема системы управления

Используя уравнения гидродинамики [5], запишем математические модели для компонентов ЗД, т.е. для системы клапанов Kл₁ и Kл₂:

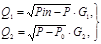(1)

где G₁, G₂ – проводимость соответствующих клапанов.

Зависимость объема воздуха в ресивере от потоков Q₁ и Q₂ находится по следующей формуле:

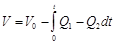. (2)

Математическая модель ЗД

Сделаем следующие допущения:

1. Зависимости проводимостей клапанов Кл₁ и Кл₂ от напряжений определяются формулами:

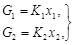(3)

где K₁, K₂ – коэффициенты чувствительности клапанов.

2. Процесс, внутри пружины манометра – изотермический.

3. Манометр измеряет относительное давление, т.е. разность между воздействующим давлением и атмосферным (равную примерно 1 кгс/см²), при воздействии атмосферного давления на манометр его показание равно 0, поэтому удобнее в математической модели использовать давление относительно атмосферного, и учитывая допущение 2 получаем следующее уравнение зависимости между давлением и объемом газа внутри пружины:

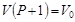, (4)

где V₀ – объем газа при атмосферном давлении.

Из уравнений (1),(3),(4) составим следующую систему уравнений:

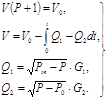(5)

Движение задвижки клапана под действием напряжения на катушке описывается следующим уравнением:

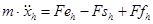. (6)

Здесь m – эффективная масса задвижки; h – номер клапана; 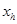, 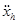– координата задвижки и её ускорение, соответственно для клапана Кл_h; Fe_h – сила магнитного поля катушки, действующая на задвижку, которая находится по формуле (7); Fs_h – сила упругости пружины, действующая на задвижку, которая находится по формуле (8), Ff _h – сила трения, вычисляется по формуле (9) [6]:

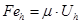, (7)

где 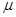– коэффициент; 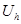– напряжение на катушке;

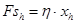, (8)

где 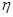– коэффициент упругости пружины;

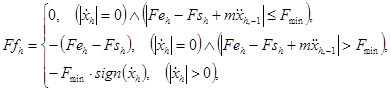(9)

где 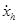– скорость движения задвижки, 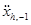– предыстория ускорения, 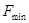– сила трения покоя.

Линеаризуем систему уравнений (5), искомыми переменными здесь являются Q₁, Q₂, V, P, задаваемые переменные G₁, G₂. Относительно этих переменных, уравнения 1, 3, 4 в системе уравнений (5) нелинейные, поэтому, для численного решения на ЭВМ, их необходимо линеаризовать. Перенесем правые части нелинейных уравнений в левую часть, обозначим их соответственно через Ф₁, Ф₃, Ф₄, и в итоге получим следующие уравнения и частные производные для функций Ф₁, Ф₃, Ф₄:

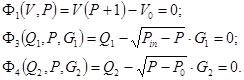
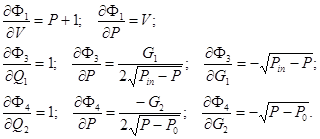(10)

Так как частные производные 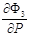и 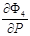стремятся к бесконечности пр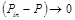и и 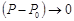, то заменим эти частные производные в окрестности особых точек P=P_in и P=P₀ на следующие выражения: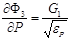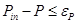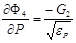

, при , , при ,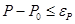

(11)

где e_P можно принять равным 0,001(P_in-P₀).

Моделируемый процесс разобьем на временные кванты dt, и представим последовательностью i–х отсчетов t_i=dt×i. Предположим, что при достаточно малом значении dt процесс изменения переменных от (i-1)-го отсчета к i-му является линейным.

Используя частные производные, запишем линеаризованные выражения для определения искомых функций и при этом учтем, что эти функции тождественно равны нулю:

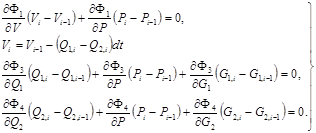
Здесь искомые переменные только Q_1,i, Q_2,i, V_i, P_i, оставим их в левой части, остальное перенесем в правую часть и в итоге получим:

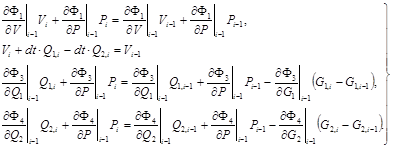(12)

Уравнение (10) в матричном виде, с учетом (8) и (9), будет выглядеть следующим образом:

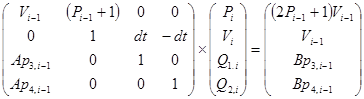, (13)

где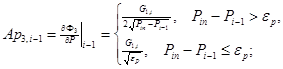

, .

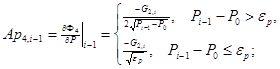
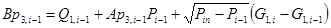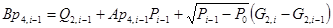Система из уравнений (6) - (9) линейна относительно переменных 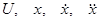для каждого случая, указанного в (9), в матричном виде эта система будет выглядеть следующим образом:

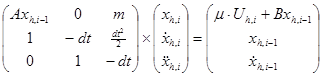, (14)

где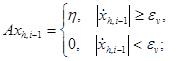

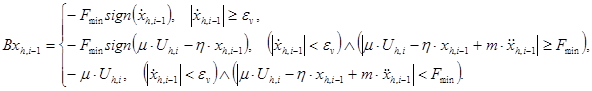
Векторы начального состояния: