Математическая модель каустики

ПРИМЕРЕ МОДЕЛИРОВАНИЕ ОПТИЧЕСКИХ СИСТЕМ В ПРИКЛАДНЫХ

ПРОГРАММАХ»

Студент 2 курса

«___»____________2017 г. _________________ Багаутдинов З.Ф.

Научный руководитель

к. физ.-мат. наук, доцент

«___»____________2017 г. __________________ А.A.Агафонов

Заведующий кафедрой

д. физ.-мат., профессор

«___»____________2017 г. __________________ Ю.Г.Игнатьев

Казань 2017

Содержание

Введение. 3

Глава I. Каустика. 4

1.1.Определение Каустики. 4

1.2.Каустики на плоскости. 5

1.3.Каустики в пространстве. 8

1.4. Математическая модель каустики. 14

1.5. Примеры каустик. 20

Глава II. Maple. 25

2.1. Общие сведения о СКМ Maple. 25

2.2. Программирование в СКМ Maple. 25

2.3. Работа с графикой. 28

Глава III. 30

3.1. Построение модели каустики для кривой второго порядка, заданной в параметрическом виде. 30

3.2. Построение модели каустики для плоскости, заданной в параметрическом виде. 35

3.3.Написание программных процедур СКМ Maple Двумерный случай. 36

Заключение. 48

Список использованной литературы.. 49

Приложение А. Программные процедуры моделирования каустик

Введение

Целью магистерской диссертации является изучение теорий каустик, оптических свойств кривых и поверхностей на примере моделирования оптических систем в СКM Maple.

Про каустики знает почти каждый из нас, кому приходилось хоть раз пить чай не из прозрачного стакана, а из чашки. Каждый из нас наблюдал, как на самом дне чашки образуются яркие линии, которые освещены намного сильнее, чем стоящие по соседству с ними точки. Также каустики можно увидеть при выжигании по дереву, когда собираешь световые лучи при помощи стекла, или при наблюдении кривых на дне какого-либо бассейна или даже ванны. Само слово каустики произошло от латинского, и в переводе означает жгучий.

Задачи выпускной квалификационной работы:

1) рассмотреть теоретический материал по теме каустик;

2) ознакомится и изучить среду Maple;

3) смоделировать оптические каустики для кривых второго и третьего порядка.

Магистерская диссертация состоит из Введения, трех глав, Заключения, Списка литературы и Приложения. Первая глава посвящена обзору теории каустик. 2-я глава охватывает обзор системы компьютерной математики Maple. В 3-ей главе описывается построение и исследование каустик для различных кривых второго и третьего порядка. В заключении кратко приведены основные результаты исследования. Приложение включает в себя код программных процедур.

Глава I. Каустика

Определение Каустики

Каустика (от лат. жгучий) - огибающая семейства лучей, не сходящихся в одной точке. Каустики в двумерном случае – это такие линии на поверхности, около которых значительно увеличивается интенсивность светового поля.

Яркие световые кривые очень интересной формы можно наблюдать на освещенном столе, на который поставлен граненый стакан с водой. Каустики в движении можно заметить на дне водоема, поверхность которого находиться в волнении. На дождевых каплях при преломлении солнечных лучей возникает каустика разных цветов - радуга. Каустики возникают в множестве других волновых явлений, а не только при рассмотрении световых явлений. Корабельные волны можно взять за каустику гравитационных волн на воде. Работы Я. Б. Зельдовича показывают, что

из-за гравитационной неустойчивости изначально почти однородное распределение массы во Вселенной собирается на каустиках и приводит к формированию нитевидной крупномасштабной структуры вселенной.

Оптические каустики в астрономии могут определять гравитационную линзу – геометрию компактного темного объекта.

В геометрической оптики каустики изображают собой линии или поверхности .

В рамках геометрической оптики каустики представляют собой линии и поверхности безгранично малой толщины. С геометрической точки зрения каустика отображает собой эволюту волнового фронта; волновой фронт — эвольвенту каустики. Если принимать к вниманию особенности света, каустики должны обладать определенной толщиной, бесспорно не меньшую, чем протяженность волны света.

Теория каустик непрерывно сопряжена с одним из направлений современной математики, это направление - теория катастроф. В дифференциальных уравнениях каустики являются опрокидыванием решений.

Каустики на плоскости

Для начала рассмотрим, что происходит, когда множество световых лучей и произвольная кривая, от которой они отражаются, находятся в одной плоскости. Достаточно демонстративным примером будет отражение лучей от окружности. Каустика, возникающая в данном случае - яркая линия с концом, находящимся между вершиной и центром зеркала (рис. 1.1).

Рисунок 1.1- Каустика при отражении от окружности

Если мы будем рассматривать параболу, то все лучи, которые будут проходить параллельно ее оси, после того как отражаться, соберутся в одной точке - эта точка будет фокусом параболы. Если говорить об окружности или других кривых это будет не так, лучи при отражении не будут сходиться в одной точке. Если рассматривать узкий пучок параллельных лучей, который падает на кривую, то после отражения от кривой он становиться сходящимся. Иначе говоря, отраженный пучок света не сходиться целиком в одной точке, но узкие пучки света, состоящие из рядом расположенных лучей, будут сходящимися. Точки пересечения, в которых будут сходиться лучи отражения, называются точками концентрации энергии, именно из этих точек и образуется каустика. При помощи данных рассуждений мы можем нарисовать каустику.

Отправим на кривую некоторое количество параллельных лучей. Разделим их отражения на пары и найдем точки пересечения лучей в каждой паре (рис.1.2).

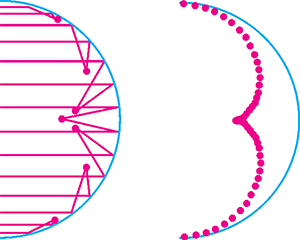
Рисунок 1.2- Слева на зеркало запущены 14 лучей, справа — 102 луча, и отмечены точки их попарного пересечения

Если начать увеличивать количество лучей, то расстояние между пересечениями парных лучей будут уменьшаться. Данные точки пересечения будут находиться с каждым разом все ближе друг к другу и на определенном этапе заполнят каустическую линию (кривую).

Рисунок 1.3- Каждый из отраженных лучей касается каустики

Мы видим один из способов того, как изучить, как устроена каустика. Можно рассмотреть еще один способ увидеть каустику - это направить множество лучей. В итоге на полученном таким образом изображении каустика будет определяться как кривая, которой при отражении касаются отраженные лучи (рис. 1.3). Это является еще одной моделью того же самого скопления световой энергии - в данном случае каждый световой луч касается каустики, что означает, что луч вдоль каустики проходит большую часть своего пути и передает ей значимую часть своей энергии. Линия, которая касается каждой прямой из некоторого семейства прямых - является огибающей этого семейства. Получается что, каустикой является огибающая световых лучей. Каустику можно назвать каркасом, на который надеты все световые лучи.

Каустики в пространстве

Все становиться на порядок сложнее и намного интересней, если рассматривать каустики в трехмерном пространстве. В трехмерном пространстве есть две точки скопления энергии. По-другому можно сказать, что поверхность каустики в пространстве состоит из пары листов.

Для примера возьмем отражающую поверхность следующего вида:

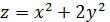(1.1)

И направим на не сверху пучок параллельно оси z. Если рассматривать плоскость y = 0, то мы получим отражение от параболы z = x², а в плоскости x = 0 отражение будет идти от параболы z = 2y². Получаться разные параболы, и лучи от них будут скапливаться на разных высотах и в разных точках по оси z. Одна из точек будет находиться на одном листе нашей каустической поверхности, а вторая на другом.

Рисунок 1.4- Отражение от пластиковых окон

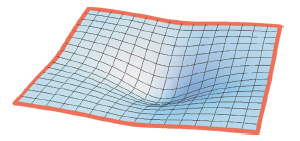
Рисунок 1.5 -За счет перепада давления стекла прогибаются внутрь

В последнее время в Интернете находят фотографии ярких четырехугольных звезд на стенах сооружений (рис. 1.4). Эти рисунки являются результатом отражения лучей солнца от пластиковых окон близ лежащих домов.

Это обусловлено тем, что в окнах из пластика между стеклами герметизируется, и воздух между ними выкачивается. Из-за перепада давления каждое из стекол деформируется внутрь и напоминает форму, продемонстрированную на рисунке 1.5 (изображение достаточно сильно растянуто вдоль вертикальной оси). Поверхность, изображенную на рисунке можно хорошо приблизить графиком следующей функции:

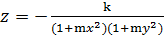(1.2)

подобрав соответствующие константы k и m.

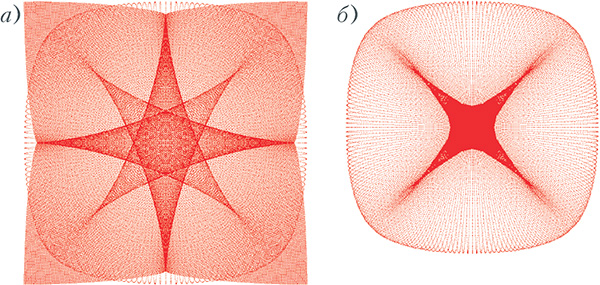
Рисунок 1.6-Изображение на экране — стене дома — при малом удалении (а) и при большем удалении (б)

Если ограничить кусок окна некоторой поверхностью и направить лучами света, направленными сверху параллельным пучком, а на пути света поставить экран, то при незначительном удалении от нашего окна мы сможем наблюдать на экране картинку, основным фрагментом этой картинки будет являться звезда, состоящая из восьми углов (рис. 1.6 (a)). Если же экран будет отодвинут на большее расстояние, то мы сможем увидеть звезду, состоящую из четырех углов, на фоне наиболее меньшего овала (рис.1.6(б)), что будет соответствовать реальным фотографиям. Четыре отсутствующих по сравнению с левым рисунком луча оказались отрезанными от звезды из-за того, что мы рассматриваем отражение только от ограниченного куска поверхности — от квадратного окна.

Рисунок 1.7- Два вида на каустическую поверхность

Теперь попробуем изобразить саму каустическую поверхность, подобную заданному каустическому изображению. Она фактически будет собрана из двух листов. На рисунке 1.7 цветом зафиксировано удаление точек каустики от заданной поверхности: синие точки находятся ближе к поверхности, красные - дальше от поверхности. Сечением одного из листов нашей каустики будет звезда из восьми углов, сечение другого будет границей окружающего звезду овала.

Рисунок 1. 8- Каустики, возникающие при преломлении света, самый яркий элемент — четырехугольная звезда

Рисунок 1. 9- Вздутие на поверхности воды, имитирующее пузырек или мениск

Каустики могут образовываться не только при отражении, но и при преломлении света, скажем на поверхности воды. На фотографиях, воспроизведенных на рисунке 1.9, солнечные лучи преломляются либо на воздушном пузырьке, либо на мениске, возникающем из-за поверхностного натяжения на иголке, погруженной в воду. И здесь, и там на дне мы видим небольшую четырехугольную звезду.

Смоделируем это явление, задав преломляющую поверхность (рис.1. 9) уравнением:

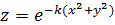(1.3)

Рисунок 1. 10- Изображение на экране - на дне сосуда

Зафиксируем постоянную k и угол падения солнечных лучей αи вспомним, что для воды показатель преломления n = 1,33. С помощью закона преломления sin α = nsin β можно рассчитать направление преломленных лучей - угол β - и, значит, построить картину, которую формируют лучи на экране, расположенном под поверхностью воды - на дне сосуда. Отчетливо видна та же самая асимметричная четырехугольная звезда (рис.1. 10), что и на фотографии см. (рис.1. 8).

Рисунок 1. 11-Каустическая поверхность, образующаяся при преломлении на воздушном пузырьке

А вот и соответствующая каустическая поверхность для преломленных лучей (рис. 1.11). Синие точки расположены ближе к поверхности воды, а красные более удалены от нее. Сечение внутренней поверхности представляет собой четырехугольную звезду, а внешней — граница овала, содержащего эту звезду.

Табл. 1. Кривые и их каустики.

Кривая	Источник света	Каустика
Окружность	На плоскости	Кардиоида
Окружность	Не на плоскости	Улитка Паскаля
Окружность	Бесконечность	Нефроида
Парабола	Лучи, перпендикулярные директрисе	Кривая третьего порядка Чирнгаузена
Кривая Чирнгаузена	Фокус	Полукубическая парабола
Циссоида Диоклеса	Фокус	Кардиоида
Кардиоида	Касп	Нефроида
Четырёхлистник	Центр	Астроида
Дельтоид	Бесконечность	Астроида
Логарифмическая спираль	Центр	Логарифмическая спираль
Циклоида	Лучи, перпендикулярные линии через каспы	1/2 Циклоиды
y = Ex	Лучи, перпендикулярные y-лучу	Цепная линия

Примеры каустик

Радуга – это частный случай каустики,игр света. Каустика представляет собой сложную, а иногда и очень красивую картину, создаваемую сходящимися световыми лучами в результате их (многократных) преломлений и отражений на поверхностях раздела сред с различной оптической плотностью. Простейшими случаями каустики являются: яркая точка света в фокусе собирающей линзы; тонкий луч прожектора, в фокусе параболического зеркала которого имеется точечный источник света; сложная световая фигура (кардиоида) внутри полого, открытого сверху цилиндра (например, чашки) при отражении света от его внутренней поверхности (рис. 1.18); дрожащие ячейки света на дне неглубокого водоёма (рис. 1.19); узкие лучи, полученные в результате отражений от поверхностей 2-го и более высоких порядков; солнечные и лунные дорожки на поверхности воды и, наконец, радуга на небе.

Рис. 1.18. Каустика в виде кардиоиды

Рис. 1.19. Каустика на дне освещённого бассейна

Значение каустик во вселенной

В настоящее время распределение вещества во Вселенной чрезвычайно неоднородно (существуют планеты. Солнце, звезды, галактики, скопления галактик и т. д.). Современная астрофизика считает, что на ранних этапах развития Вселенной таких неоднородностей не было. Как же они сформировались? Я. Б. Зельдович в 1970 г. предложил объяснение образования скоплений пылевидной материи, математически эквивалентное анализу возникновения особенностей каустик, начатому в 1963 г. Е. М. Лифшицем, Халатниковым и Судаковым.

Рассмотрим бесстолкновительную среду, т. е. среду настолько разреженную, что ее частицы проходят друг "сквозь" друга, не сталкиваясь. Предположим, для простоты, что частицы не взаимодействуют и движутся по инерции: через какое-то время t частица, находившаяся в точке х, перейдет в точку х + vt.

Предположим, что в начальный момент скорость частицы, находящейся в точке х, была v₀ (х); векторное поле v₀ называется начальным полем скоростей среды. С течением времени частицы будут двигаться, и поле скоростей будет меняться (хотя скорость каждой частицы и не меняется, в следующий момент времени эта частица находится на новом месте).

На рисунке 1.20 показано начальное поле скоростей одномерной среды v₀ и получающиеся из него через время t = 1, 2 и 3 ноля v₁, v₂, v₃. Мы наблюдаем, что, начиная с определенного момента, более быстрые частицы начинают обгонять более медленные; в результате чего, поле скоростей становится трехзначным: через одну точку пространства три потока частиц проходят с разной скоростью.

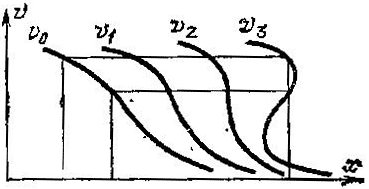
Рисунок 1.20- Эволюция поля скоростей бесстолкновительной среды

Движение нашей среды можно описать как однопараметрическое семейство отображений прямой на прямую. Собственно для каждого t определено отображение g_t, переводящее начальное положение частицы (х) в конечное: g_t = х + v₀ (х)t.

Отображение g₀ является тождественным преобразованием, оставляющим каждую точку на месте. Отображения, соответствующие моментам t, близким к 0, взаимно однозначны и не имеют особенностей. После момента первого обгона отображение g_t имеет две складки.

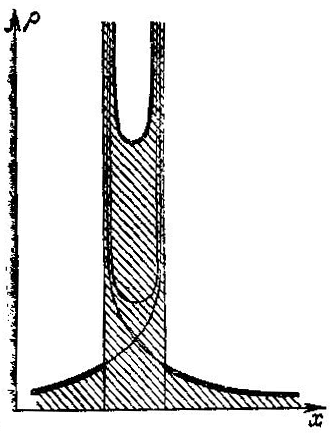
Рисунок 1.21- Особенности плотности после обгона

Пусть в начальный момент плотность среды в точке х была ρ₀(х), Со временем плотность изменится. Легко догадаться, что после обгона график плотности будет иметь вид (на расстоянии 8 от точки складки плотность оказывается порядка 1/√ε).

Исходя из этого, небольшие отличия начального ноля скоростей от постоянного приводят через достаточно большое время к образованию скоплений частиц (в местах бесконечно большой плотности).

Глава II. Maple

Для построения каустик, используется система компьютерной математики Maple (ver. 17) о которой и будет идти речь в этой главе.

Общие сведения о СКМ Maple

Maple-это система компьютерной математики созданная для символьных вычислений, работы с математическими выражениями в разных формах.

Система компьютерной математики является мощным инструментом для выполнения вычислений и работы с разными формами математических и аналитических расчетов. Данная система может быть применена в образовательных и научных целях.

Работа с графикой

Для того чтобы построить график или нарисовать рисунок, включая анимированных графиков и рисунков, в СКM Maple существует большое количество разнообразных команд. Множество из них требует того, чтобы был вызван пакет, включающий данную команду. Несложные графики можно построить тривиальным оператором plot. Для оператора plot не нужно подключение каких-либо команд. Для него не нужно дополнительных средств.

Приведем некоторые простые варианты для построения графиков функций.

•График элементарных функций; plot(cos). В данной команде указание аргумента не обязательно. (рис.2.1).

Например, такие не очень привычные выражения, как plot(sin+cos). Такие математические высказывания случат либо как демонстративный материал, либо как не очень сложный справочный. Довольно нечасто такие виды обращений используют для оператора plot.

• График (рис.2.2) функции y = sin(x) с обозначением пределов x=0..2*Pi и обрезанием системы координат(0..0.8):

plot(sin(x),x=0..2*Pi,0..0.8).

Если не фиксировать ограничения по оси, то на графике будет показан весь график (если он не определен на бесконечности).

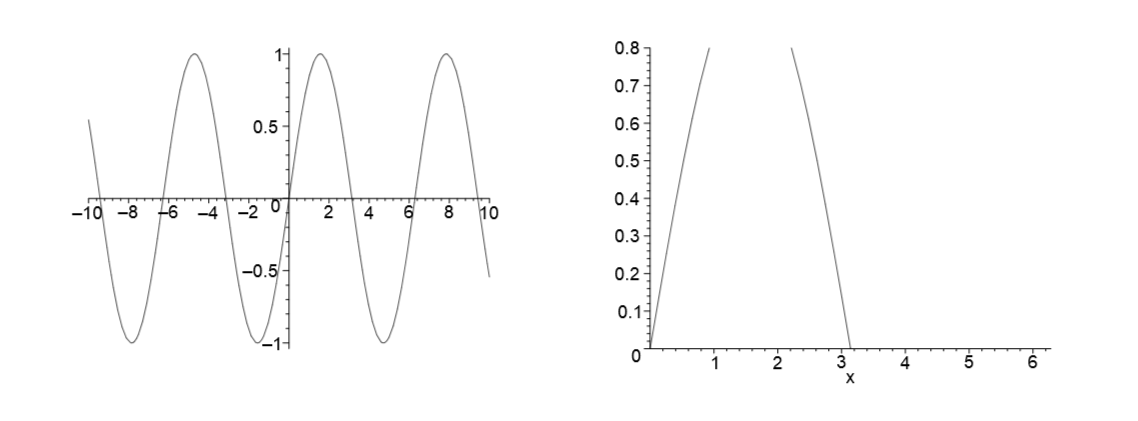
Рисунок 2.1-График функций y = sin(x) Рисунок 2.2- График функций y = sin(x)
с ограничениями

Глава III.

Трехмерный случай

Отражение на плоскости будем рассматривать на примере параболоида.

Задаем начальные условия для прямой:

x[0]:=0:

y[0]:=0:

z[0]:=0:

ax:=1:

ay:=-.3:

az:=10:

Задаем уравнение плоскости и уравнения прямой:

a:=x^2+y^2-z;

b:=x-x[0]/ax=y-y[0]/ay;

c:=y-y[0]/ay=(z-z[0])/az;

Рисуем прямую и параболоид:

pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-10..10):

pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):

Находим точку пересечения прямой и плоскости:

sol:=evalf(solve({a,b,c},{x,y,z}));

x_:=evalf(subs(sol,x));

y_:=evalf(subs(sol,y));

z_:=evalf(subs(sol,z));

pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-1..1):

pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):

pl_c:=pointplot3d([x_,y_,z_],color=red);

Находим производные в точках :

x1:=subs({x=x_,y=y_,z=z_},diff(a,x)):

y1:=subs({x=x_,y=y_,z=z_},diff(a,y)):

z1:=subs({x=x_,y=y_,z=z_},diff(a,z)):

Вектор прямой задается следующим образом:

l:=[ax,ay,az];

Вектор нормали задается следующим образом:

n1:=[x1,y1,z1];4

Уравнение нормали и вывод:

pl_e:=spacecurve([x1*t+x_,y1*t+y_,z1*t+z_],t=-8..4,color=green):

Аналогично двумерному случаю находим вектор отражения при помощи вектора падения луча и вектора нормали:

k:=dotprod(l,n1)/dotprod(n1,n1);
p:=[2*k*n1[1],2*k*n1[2],2*k*n1[3]];

r:=l-p;

Вектор l будет вектором отражения.

Задаем уравнение отраженного луча, и обозначаем его:

b1:=(x-x_)/r[1]=(y-y_)/r[2];

c1:=(y-y_)/r[2]=(z-z_)/r[3];

pl_d:=spacecurve([r[1]*t+x_,r[2]*t+y_,r[3]*t+z_],t=-1..1,color=yellow):

Выводим луч падения (фиолетовый), нормаль (зеленая), отраженный луч (желтый) (Рис.3.8).

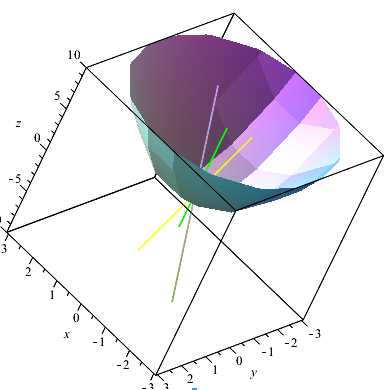
Рисунок 3.8-Отражение луча от плоскости.

Заключение

В ходе данной работы был рассмотрен теоретический материал по теме каустик и были изучены их свойства .Также в ходе магистерской диссертации была изучена среда СКМ Maple. Была создана процедура для моделирования каустик для кривых второго порядка.

Таким образом, цели, поставленные в квалификационной работе, выполнены.

Список использованной литературы

1. Burridge, R. Asymptotic evaluation of integrals related to time-domain fields near caustics, SIAM J. Appl. Math., 55:2, 1995.

2. Андреев, А.Н. Каустики на плоскости/ А.Н. Андреев, А.А. Панов «Квант» -2010. -№3.

3. Арнольд, В. И. Особенности каустик и волновых фронтов, В.И. Арнольд - М.: Фазис, 1996.

4. Арнольд, В. И. Теория катастроф / Арнольд В. И. М.: Наука, 1990.

5. Баев, А. В. Математическое моделирование волн в слоистых средах вблизи каустики/ А. В. Баев// Матем. Моделирование-2013- 25:12-С.83-102

6. Гольдин, С.В. Сейсмическое волновое поле в близи каустик: анализ во временной области/ С.В. Гольдин, А.А. Дучков //Физика Земли. - 2002.- №7. С.56–66.

7. Дьяконов, В.П. Maple 9.5/10 в математике, физике и образовании/ В.П. Дьяконов- М.: СОЛОН-Пресс, 2006. - 720 с.

8. Кирсанов, М. Н. Задачи по теоретической механике с решениями в Maple 11. М.: Физматлит, 2010, 264с.

9. Кирсанов, М.Н. Maple и Maplet. Решения задач механики / Кирсанов М.Н.-М.: Лань, 2012. -512с.

10. Лонгейр, М. Крупномасштабная структура Вселенной/ Ред. М. Лонгейр, Я. Эйнасто. - М.: Мир, 1981.

11. Постон, Т. Теория катастроф и ее применения/ Постон Т., Стюарт И. - М.: Мир, 1980.

12. Яновская, Т.Б. Численный метод расчета поля поверхностной волны при наличии каустик / Яновская Т.Б., Гейгер М.А.//Физика Земли. - 2007.

Приложение А. Программные процедуры моделирования каустик

#Отражение от произвольной кривой(параллельное падение лучей)

> restart:

with(plots):

with(plottools):

> prbRefLines:=proc(L,h,d1,d2,N)

global Line_;

local dh,dir,i;

dir:=[d1,d2]:

dh:=(h/N):

for i from 1 to N do

Line_[i]:=[[L,-h/2+(i-1)*dh],dir,[0,0],[0,0]];

end do:

end proc:

> prbRefLines(5,10,-1,-.1,50);

eval(Line_):

> prbRefArray:=proc(p,L,N)

global Line_:

local dir_,x,y,a_,r1,tmp1,kas,per1,per2,norm,l,n1,n2,k,i,dr;

#print(Line_[1]);

# вектор направления

for i from 1 to N do

#print(Line_[i][2][1]):

Line_[i][2][2]:

# расчет пересечения:

a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:

if Line_[i][2][1]=0 then

a_:=x=Line_[i][1][1]:

else

a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:

end if:

#print(a_);

r1:=[t^2/(2*p),t]:

solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k}):

tmp1:=solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k});

y[1]:=rhs(tmp1[1][2]):

x[1]:=subs(t=rhs(tmp1[1][2]),r1[1]):

y[2]:=rhs(tmp1[2][2]):

x[2]:=subs(t=rhs(tmp1[2][2]),r1[1]):

per1:=sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2):

per2:=sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2):

#print([per1,per2]):

if evalf(sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2))<evalf(sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)) then

Line_[i][3][1]:=x[1]

else Line_[i][3][1]:=x[2]

end if:

if evalf(sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2))<evalf(sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)) then

Line_[i][3][2]:=y[1]

else Line_[i][3][2]:=y[2]

end if:

# Нормаль в новой точке

dr:=diff(r1,t):

kas:=evalf(subs(t=Line_[i][3][2],dr)):

norm:=[kas[2],-kas[1]]:

if evalf(norm[1]*(Line_[i][1][1]-Line_[i][2][1])+norm[2]*(Line_[i][1][2]-Line_[i][2][2]))<0 then norm:=[-kas[2],kas[1]]:

end if;

#norm1:

#Вектор направления отражения

n1:=(Line_[i][2][1]*norm[1]+Line_[i][2][2]*norm[2])/(norm[1]*norm[1]+norm[2]*norm[2]):

n2:=[norm[1]*2*n1,norm[2]*2*n1]:

l:=[Line_[i][2][1]-n2[1],Line_[i][2][2]-n2[2]]:

#точка отраженная

Line_[i][4][1]:=l[1]:

Line_[i][4][2]:=l[2]:

end do:

end proc:

> prbRefArray(60,10,50):

> pprbLines:=proc(p,L,h,N)

local pltprb,pltLines,pltLines1,r1;

#

r1:=[t^2/(2*p),t]:

print(r1);

pltprb:=plot([op(r1),t=-10..10],scaling=constrained,

color=black,

thickness=3):

#

pltLines:=display(

seq(

line(

Line_[i][1],

Line_[i][3],

color=red),

i=1..N),

insequence=false,

scaling=constrained

);

pltLines1:=display(

seq(

line(

Line_[i][3],

Line_[i][4],

color=red),

i=1..N),

insequence=false,

scaling=constrained

);

display([pltLines,pltprb,pltLines1],scaling=constrained,axes=none);

end proc:

> pprbLines(60,200,10,10);

#Отражение от произвольной кривой(пучок лучей)

> restart:

with(plots):

with(plottools):

> r1:=[t^2/(200),t]:

t1:=-20:

t2:=20:

> prbRefLines:=proc(L,h,N)

global Line_, r1;

local dh,dir,i,dL;

dL:=L/2;

dh:=(h/N):

for i from 1 to N do

Line_[i]:=[[L,0],[L-dL-L,-h/2+(i-1)*dh],[0,0],[0,0]];

end do:

end proc:

> prbRefLines(5,10,5);

> prbRefArray:=proc(L,N)

global Line_, r1:

local dir_,x,y,a_,tmp1,kas,per1,per2,norm,l,n1,n2,k,i,dr;

# вектор направления

for i from 1 to N do

# расчет пересечения:

a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:

if Line_[i][2][1]=0 then

a_:=x=Line_[i][1][1]:

else

a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:

end if:

solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k}):

tmp1:=evalf(solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k})):

Line_[i][3][1]:=subs(k=rhs(tmp1[1]),a_[1]):

Line_[i][3][2]:=subs(k=rhs(tmp1[1]),a_[2]):

dr:=diff(r1,t):

kas:=evalf(subs(t=Line_[i][3][2],dr)):

norm:=[kas[2],-kas[1]]:

if evalf(norm[1]*(Line_[i][1][1]-Line_[i][2][1])+norm[2]*(Line_[i][1][2]-Line_[i][2][2]))<0 then norm:=[-kas[2],kas[1]]:

end if:

#Вектор направления отражения

n1:=(Line_[i][2][1]*norm[1]+Line_[i][2][2]*norm[2])/(norm[1]*norm[1]+norm[2]*norm[2]):

n2:=[norm[1]*2*n1,norm[2]*2*n1]:

l:=[Line_[i][2][1]-n2[1],Line_[i][2][2]-n2[2]]:

#точка отраженная

Line_[i][4][1]:=l[1]:

Line_[i][4][2]:=l[2]:

end do:

end proc:

> prbRefArray(10,5):

> pprbLines:=proc(L,h,N)

global r1,t1,t2:

local pltprb,pltLines,pltLines1;

pltprb:=plot([op(r1),t=t1..t2],scaling=constrained,

color=black,

thickness=3):

pltLines:=display(

seq(

line(

Line_[i][1],

Line_[i][3],

color=red),

i=1..N),

insequence=false,

scaling=constrained

);

pltLines1:=display(

seq(

line(

Line_[i][3],

2*Line_[i][4],

color=green),

i=1..N),

insequence=false,

scaling=constrained

);

display([pltLines,pltprb,pltLines1],scaling=constrained,axes=none);

end proc:

> pprbLines(1,20,1);

> pprbLines(200,.5,2):

> Mainproc:=proc(L,h,N)

global r1,t1,t2:

prbRefLines(L,h,N):

prbRefArray(L,N):

pprbLines(L,h,N):

end proc:

> Mainproc(100,20,10);

#Отражение от параметрически заданной плоскости

restart:

with(plots):

with(plottools):

with(linalg):

x[0]:=0:

y[0]:=0:

z[0]:=0:

ax:=1:

ay:=-.3:

az:=10:

a:=x^2+y^2-z;

b:=x-x[0]/ax=y-y[0]/ay;

c:=y-y[0]/ay=(z-z[0])/az;

diff(a,y);

pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-10..10,color=black):

pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):

display([pl_a,pl_b]);

sol:=evalf(solve({a,b,c},{x,y,z}));

x_:=evalf(subs(sol,x));

y_:=evalf(subs(sol,y));

z_:=evalf(subs(sol,z));

pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-1..1):

pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):

pl_c:=pointplot3d([x_,y_,z_],color=red);

display([pl_a,pl_b,pl_c]);

x1:=subs({x=x_,y=y_,z=z_},diff(a,x)):

y1:=subs({x=x_,y=y_,z=z_},diff(a,y)):

z1:=subs({x=x_,y=y_,z=z_},diff(a,z)):

l:=[ax,ay,az];

n1:=[x1,y1,z1];

pl_e:=spacecurve([x1*t+x_,y1*t+y_,z1*t+z_],t=-8..4,color=green):

n1[1];

k:=dotprod(l,n1)/dotprod(n1,n1);

p:=[2*k*n1[1],2*k*n1[2],2*k*n1[3]];

r:=l-p;

b1:=(x-x_)/r[1]=(y-y_)/r[2];

c1:=(y-y_)/r[2]=(z-z_)/r[3];

pl_d:=spacecurve([r[1]*t+x_,r[2]*t+y_,r[3]*t+z_],t=-1..1,color=yellow):

display([pl_a,pl_b,pl_d,pl_e]);

#Частные случаи изображения каустики
> restart:

with(plots):

with(plottools):

> r:=[u,u^2];

r[2];

> pl_a:=plot([op(r),u=-4..4],scaling=constrained);

> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

> l:=[cx,cy];

> pl_b:=plot([op(l),u=-0.7..0.7],scaling=constrained,color=blue);

> display([pl_a,pl_b]);

> restart:

with(plots):

with(plottools):

> a:=2;

b:=3;

> r:=[a*cos(u),b*sin(u)];

r[2];

> pl_a:=plot([op(r),u=1/2*Pi..3/2*Pi],scaling=constrained);

plot([op(r),u=1/2*Pi..3/2*Pi],scaling=constrained);

> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

> l:=[cx,cy];

> pl_b:=plot([op(l),u=-4..4],scaling=constrained,color=blue);

> display([pl_a,pl_b]);

> restart:

with(plots):

with(plottools):

> a:=6;

b:=20;

> r:=[a*cosh(u),b*sinh(u)];

r[2];

> pl_a:=plot([op(r),u=-2*Pi..2*Pi],scaling=constrained);

plot([op(r),u=-2*Pi..2*Pi],scaling=constrained);

> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));

> l:=[cx,cy];

> pl_b:=plot([op(l),u=-2..2],scaling=constrained,color=blue);

> display([pl_a,pl_b]);

ПРИМЕРЕ МОДЕЛИРОВАНИЕ ОПТИЧЕСКИХ СИСТЕМ В ПРИКЛАДНЫХ

ПРОГРАММАХ»

Студент 2 курса

«___»____________2017 г. _________________ Багаутдинов З.Ф.

Научный руководитель

к. физ.-мат. наук, доцент

«___»____________2017 г. __________________ А.A.Агафонов

Заведующий кафедрой

д. физ.-мат., профессор

«___»____________2017 г. __________________ Ю.Г.Игнатьев

Казань 2017

Содержание

Введение. 3

Глава I. Каустика. 4

1.1.Определение Каустики. 4

1.2.Каустики на плоскости. 5

1.3.Каустики в пространстве. 8

1.4. Математическая модель каустики. 14

1.5. Примеры каустик. 20

Глава II. Maple. 25

2.1. Общие сведения о СКМ Maple. 25

2.2. Программирование в СКМ Maple. 25

2.3. Работа с графикой. 28

Глава III. 30

3.1. Построение модели каустики для кривой второго порядка, заданной в параметрическом виде. 30

3.2. Построение модели каустики для плоскости, заданной в параметрическом виде. 35

3.3.Написание программных процедур СКМ Maple Двумерный случай. 36

Заключение. 48

Список использованной литературы.. 49

Приложение А. Программные процедуры моделирования каустик

Введение

Целью магистерской диссертации является изучение теорий каустик, оптических свойств кривых и поверхностей на примере моделирования оптических систем в СКM Maple.

Про каустики знает почти каждый из нас, кому приходилось хоть раз пить чай не из прозрачного стакана, а из чашки. Каждый из нас наблюдал, как на самом дне чашки образуются яркие линии, которые освещены намного сильнее, чем стоящие по соседству с ними точки. Также каустики можно увидеть при выжигании по дереву, когда собираешь световые лучи при помощи стекла, или при наблюдении кривых на дне какого-либо бассейна или даже ванны. Само слово каустики произошло от латинского, и в переводе означает жгучий.

Задачи выпускной квалификационной работы:

1) рассмотреть теоретический материал по теме каустик;

2) ознакомится и изучить среду Maple;

3) смоделировать оптические каустики для кривых второго и третьего порядка.

Магистерская диссертация состоит из Введения, трех глав, Заключения, Списка литературы и Приложения. Первая глава посвящена обзору теории каустик. 2-я глава охватывает обзор системы компьютерной математики Maple. В 3-ей главе описывается построение и исследование каустик для различных кривых второго и третьего порядка. В заключении кратко приведены основные результаты исследования. Приложение включает в себя код программных процедур.

Глава I. Каустика

Определение Каустики

Каустика (от лат. жгучий) - огибающая семейства лучей, не сходящихся в одной точке. Каустики в двумерном случае – это такие линии на поверхности, около которых значительно увеличивается интенсивность светового поля.

Яркие световые кривые очень интересной формы можно наблюдать на освещенном столе, на который поставлен граненый стакан с водой. Каустики в движении можно заметить на дне водоема, поверхность которого находиться в волнении. На дождевых каплях при преломлении солнечных лучей возникает каустика разных цветов - радуга. Каустики возникают в множестве других волновых явлений, а не только при рассмотрении световых явлений. Корабельные волны можно взять за каустику гравитационных волн на воде. Работы Я. Б. Зельдовича показывают, что

из-за гравитационной неустойчивости изначально почти однородное распределение массы во Вселенной собирается на каустиках и приводит к формированию нитевидной крупномасштабной структуры вселенной.

Оптические каустики в астрономии могут определять гравитационную линзу – геометрию компактного темного объекта.

В геометрической оптики каустики изображают собой линии или поверхности .

В рамках геометрической оптики каустики представляют собой линии и поверхности безгранично малой толщины. С геометрической точки зрения каустика отображает собой эволюту волнового фронта; волновой фронт — эвольвенту каустики. Если принимать к вниманию особенности света, каустики должны обладать определенной толщиной, бесспорно не меньшую, чем протяженность волны света.

Теория каустик непрерывно сопряжена с одним из направлений современной математики, это направление - теория катастроф. В дифференциальных уравнениях каустики являются опрокидыванием решений.

Каустики на плоскости

Для начала рассмотрим, что происходит, когда множество световых лучей и произвольная кривая, от которой они отражаются, находятся в одной плоскости. Достаточно демонстративным примером будет отражение лучей от окружности. Каустика, возникающая в данном случае - яркая линия с концом, находящимся между вершиной и центром зеркала (рис. 1.1).

Рисунок 1.1- Каустика при отражении от окружности

Если мы будем рассматривать параболу, то все лучи, которые будут проходить параллельно ее оси, после того как отражаться, соберутся в одной точке - эта точка будет фокусом параболы. Если говорить об окружности или других кривых это будет не так, лучи при отражении не будут сходиться в одной точке. Если рассматривать узкий пучок параллельных лучей, который падает на кривую, то после отражения от кривой он становиться сходящимся. Иначе говоря, отраженный пучок света не сходиться целиком в одной точке, но узкие пучки света, состоящие из рядом расположенных лучей, будут сходящимися. Точки пересечения, в которых будут сходиться лучи отражения, называются точками концентрации энергии, именно из этих точек и образуется каустика. При помощи данных рассуждений мы можем нарисовать каустику.

Отправим на кривую некоторое количество параллельных лучей. Разделим их отражения на пары и найдем точки пересечения лучей в каждой паре (рис.1.2).